《2025年中学生世界八年级数学上册沪教版五四制》

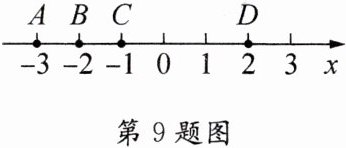
9. 如图,数轴上的A、B、C、D四点中,与数$-\sqrt{3}$表示的点最接近的是点B.

答案： 【解析】：
本题可先确定$-\sqrt{3}$的取值范围，再结合数轴上各点的位置，判断哪个点与$-\sqrt{3}$最接近。
步骤一：确定$-\sqrt{3}$的取值范围
因为$1\lt 3\lt 4$，根据算术平方根的性质：若$a\lt b$，且$a\geq0,b\geq0$，则$\sqrt{a}\lt\sqrt{b}$，可得$\sqrt{1}\lt\sqrt{3}\lt\sqrt{4}$，即$1\lt\sqrt{3}\lt 2$。
不等式两边同时乘以$-1$，不等号方向改变，所以$-2\lt -\sqrt{3}\lt -1$。
步骤二：分析数轴上各点的位置
观察数轴可知，点$A$在$-3$的位置，点$B$在$-2$和$-1$之间且更靠近$-2$，点$C$在$-1$的位置，点$D$在$2$的位置。
步骤三：判断与$-\sqrt{3}$最接近的点
由于$-2\lt -\sqrt{3}\lt -1$，且$-\sqrt{3}$更接近$-2$与$-1$的中间值，而点$B$在$-2$和$-1$之间且更靠近$-2$，所以与数$-\sqrt{3}$表示的点最接近的是点$B$。
【答案】：$B$

10. 估计$\sqrt{6}+1$在数轴上的点,在表示两相邻整数3和4所对应的点之间.

答案： 【解析】：
本题主要考察对无理数的估算以及数轴上的点的位置判断。
首先，我们需要找到两个完全平方数，使得6位于它们之间。
易得，$4 ＜ 6 ＜ 9$。
对这三个数分别开方，得到：
$\sqrt{4} ＜ \sqrt{6} ＜ \sqrt{9}$
即：
$2 ＜ \sqrt{6} ＜ 3$
然后，两边同时加1，得到：
$2 + 1 ＜ \sqrt{6} + 1 ＜ 3 + 1$
即：
$3 ＜ \sqrt{6} + 1 ＜ 4$
由此，我们可以判断$\sqrt{6} + 1$在数轴上的点位于表示3和4所对应的点之间。
【答案】：
3；4。

11. 如图,将下列各数与数轴上$A$、$B$、$C$、$D$、$E$五个点对应起来:
$-2$、$\sqrt{3}$、$-\pi$、$\sqrt[3]{10}$、$\frac{3}{2}$.

答案： 解：
$-\pi\approx-3.14$，对应点$A$；
$-2$对应点$B$；
$\frac{3}{2}=1.5$，对应点$C$；
$\sqrt{3}\approx1.732$，对应点$D$；
$\sqrt[3]{10}\approx2.154$，对应点$E$。
结论：$A:-\pi$，$B:-2$，$C:\frac{3}{2}$，$D:\sqrt{3}$，$E:\sqrt[3]{10}$。

12. 如图①,将由五个边长为$1$的小正方形拼成的图形沿虚线剪开,并按如图②所示的方式重新拼成一个大的正方形.
(1)求图②中大正方形的边$AB$的长;
(2)根据上述过程,你能否在如图③所示的数轴中,找到表示$\sqrt{5}和-\sqrt{5}$的数?

答案：
(1)解：由题意，五个小正方形的面积和为$5×1×1 = 5$，即大正方形面积为$5$。设大正方形边长$AB = x$，则$x^{2}=5$，$x=\sqrt{5}$（边长为正，舍去负值），故$AB=\sqrt{5}$。
(2)解：在数轴上，以原点$O$为起点，在正半轴取$OA = 2$（单位长度），过$A$作数轴垂线，截取$AB = 1$（单位长度），连接$OB$，由勾股定理得$OB=\sqrt{2^{2}+1^{2}}=\sqrt{5}$。以$O$为圆心，$OB$长为半径画弧，交数轴正半轴于点$P$，则点$P$表示$\sqrt{5}$；交数轴负半轴于点$Q$，则点$Q$表示$-\sqrt{5}$。