1. 下列四个数中,负数是 (
A.$|-2|$;
B.$(-2)^{2}$;
C.$-\sqrt{2}$;
D.$\sqrt{(-2)^{2}}$.
C
)A.$|-2|$;
B.$(-2)^{2}$;
C.$-\sqrt{2}$;
D.$\sqrt{(-2)^{2}}$.
答案:
【解析】:
本题主要考察负数的定义以及绝对值、平方、平方根的基本数学概念。
A选项,$|-2|$,根据绝对值的定义,绝对值表示一个数距离0的距离,所以$|-2|=2$,是正数,不符合题意。
B选项,$(-2)^{2}$,根据平方的定义,一个数的平方就是这个数乘以它自己,所以$(-2)^{2}=4$,是正数,不符合题意。
C选项,$-\sqrt{2}$,这里的负号表示取反,$\sqrt{2}$是一个正的无理数,所以$-\sqrt{2}$是负数,符合题意。
D选项,$\sqrt{(-2)^{2}}$,先计算$(-2)^{2}=4$,再取平方根,得到$\sqrt{4}=2$,是正数,不符合题意。
综上所述,只有C选项是负数。
【答案】:
C
本题主要考察负数的定义以及绝对值、平方、平方根的基本数学概念。
A选项,$|-2|$,根据绝对值的定义,绝对值表示一个数距离0的距离,所以$|-2|=2$,是正数,不符合题意。
B选项,$(-2)^{2}$,根据平方的定义,一个数的平方就是这个数乘以它自己,所以$(-2)^{2}=4$,是正数,不符合题意。
C选项,$-\sqrt{2}$,这里的负号表示取反,$\sqrt{2}$是一个正的无理数,所以$-\sqrt{2}$是负数,符合题意。
D选项,$\sqrt{(-2)^{2}}$,先计算$(-2)^{2}=4$,再取平方根,得到$\sqrt{4}=2$,是正数,不符合题意。
综上所述,只有C选项是负数。
【答案】:
C
2. 下列说法正确的是 (
A.$-3是(-3)^{2}$的算术平方根;
B.$-9的算术平方根是-3$;
C.因为$(-4)^{2}= 16$,所以$-4是16$的算术平方根;
D.$1$的算术平方根是它本身.
D
)A.$-3是(-3)^{2}$的算术平方根;
B.$-9的算术平方根是-3$;
C.因为$(-4)^{2}= 16$,所以$-4是16$的算术平方根;
D.$1$的算术平方根是它本身.
答案:
【解析】:
本题主要考察算术平方根的定义及性质。
A. 对于$(-3)^{2}$,其值为9。但9的算术平方根是3,不是-3。因为算术平方根定义为非负数,所以A选项错误。
B. 对于-9,它没有算术平方根,因为任何实数的平方都是非负的,所以不可能找到一个实数,其平方为-9。所以B选项错误。
C. 虽然$(-4)^{2}$确实等于16,但16的算术平方根是4,不是-4。算术平方根总是非负的。所以C选项错误。
D. 1的算术平方根是1,这符合算术平方根的定义,因为$1^2 = 1$。所以D选项正确。
【答案】:
D
本题主要考察算术平方根的定义及性质。
A. 对于$(-3)^{2}$,其值为9。但9的算术平方根是3,不是-3。因为算术平方根定义为非负数,所以A选项错误。
B. 对于-9,它没有算术平方根,因为任何实数的平方都是非负的,所以不可能找到一个实数,其平方为-9。所以B选项错误。
C. 虽然$(-4)^{2}$确实等于16,但16的算术平方根是4,不是-4。算术平方根总是非负的。所以C选项错误。
D. 1的算术平方根是1,这符合算术平方根的定义,因为$1^2 = 1$。所以D选项正确。
【答案】:
D
3. 下列计算错误的是 (
A.$\sqrt[3]{64}= 4$;
B.$-\sqrt[3]{-64}= 4$;
C.$\sqrt[3]{-64}= 4$;
D.$\pm\sqrt[3]{-64}= \pm4$.
C
)A.$\sqrt[3]{64}= 4$;
B.$-\sqrt[3]{-64}= 4$;
C.$\sqrt[3]{-64}= 4$;
D.$\pm\sqrt[3]{-64}= \pm4$.
答案:
【解析】:
本题主要考察立方根的计算。
对于选项A:
因为$4^3 = 64$,
所以$\sqrt[3]{64} = 4$,正确。
对于选项B:
因为$(-4)^3 = -64$,所以$\sqrt[3]{-64} = -4$,
再取负值得$-\sqrt[3]{-64} = 4$,正确。
对于选项C:
直接计算得$\sqrt[3]{-64} = -4$,与选项C中的$\sqrt[3]{-64} = 4$不符,错误。
对于选项D:
因为$(-4)^3 = -64$,所以$\sqrt[3]{-64} = -4$,同时考虑到正负的平方根都有两个解,
所以$\pm\sqrt[3]{-64} = \pm4$,正确。
综上所述,计算错误的是选项C。
【答案】:
C
本题主要考察立方根的计算。
对于选项A:
因为$4^3 = 64$,
所以$\sqrt[3]{64} = 4$,正确。
对于选项B:
因为$(-4)^3 = -64$,所以$\sqrt[3]{-64} = -4$,
再取负值得$-\sqrt[3]{-64} = 4$,正确。
对于选项C:
直接计算得$\sqrt[3]{-64} = -4$,与选项C中的$\sqrt[3]{-64} = 4$不符,错误。
对于选项D:
因为$(-4)^3 = -64$,所以$\sqrt[3]{-64} = -4$,同时考虑到正负的平方根都有两个解,
所以$\pm\sqrt[3]{-64} = \pm4$,正确。
综上所述,计算错误的是选项C。
【答案】:
C
4. 估计$35的立方根a$的大小是 (
A.$2 < a < 3$;
B.$3 < a < 4$;
C.$4 < a < 5$;
D.$5 < a < b$.
B
)A.$2 < a < 3$;
B.$3 < a < 4$;
C.$4 < a < 5$;
D.$5 < a < b$.
答案:
【解析】:
本题主要考察立方根的定义以及数的估计。为了找到$35$的立方根$a$所在的范围,我们需要找到两个连续的整数,它们的立方分别小于和大于$35$。
首先,我们计算几个整数的立方:
$2^3 = 8$,
$3^3 = 27$,
$4^3 = 64$,
由于$27 \lt 35 \lt 64$,
我们可以推断出$3 \lt \sqrt[3]{35} \lt 4$,
即$3 \lt a \lt 4$。
【答案】:
B.$3 < a < 4$。
本题主要考察立方根的定义以及数的估计。为了找到$35$的立方根$a$所在的范围,我们需要找到两个连续的整数,它们的立方分别小于和大于$35$。
首先,我们计算几个整数的立方:
$2^3 = 8$,
$3^3 = 27$,
$4^3 = 64$,
由于$27 \lt 35 \lt 64$,
我们可以推断出$3 \lt \sqrt[3]{35} \lt 4$,
即$3 \lt a \lt 4$。
【答案】:
B.$3 < a < 4$。
5. 已知$\sqrt{20n}$是整数,则满足条件的最小正整数$n$是 (
A.$2$;
B.$3$;
C.$4$;
D.$5$.
D
)A.$2$;
B.$3$;
C.$4$;
D.$5$.
答案:
【解析】:
本题主要考察二次根式的性质以及完全平方数的知识。
首先,我们将给定的根式$\sqrt{20n}$进行因式分解,得到$\sqrt{20n} = \sqrt{4 × 5 × n} = 2\sqrt{5n}$。
由于题目要求$\sqrt{20n}$是整数,那么$2\sqrt{5n}$也必须是整数。这就意味着$\sqrt{5n}$必须是整数,即$5n$必须是一个完全平方数。
接下来,我们需要找到满足条件的最小正整数$n$,使得$5n$是一个完全平方数。
考虑选项中的值,当$n=5$时,$5n=25$,此时$25$是一个完全平方数,满足条件。
而当$n=2$,$3$或$4$时,$5n$均不是完全平方数,不满足条件。
因此,满足条件的最小正整数$n$是$5$。
【答案】:
D
本题主要考察二次根式的性质以及完全平方数的知识。
首先,我们将给定的根式$\sqrt{20n}$进行因式分解,得到$\sqrt{20n} = \sqrt{4 × 5 × n} = 2\sqrt{5n}$。
由于题目要求$\sqrt{20n}$是整数,那么$2\sqrt{5n}$也必须是整数。这就意味着$\sqrt{5n}$必须是整数,即$5n$必须是一个完全平方数。
接下来,我们需要找到满足条件的最小正整数$n$,使得$5n$是一个完全平方数。
考虑选项中的值,当$n=5$时,$5n=25$,此时$25$是一个完全平方数,满足条件。
而当$n=2$,$3$或$4$时,$5n$均不是完全平方数,不满足条件。
因此,满足条件的最小正整数$n$是$5$。
【答案】:
D
6. 若$\sqrt{m^{2}}= 5$,则$m= $
$\pm 5$
;若$\sqrt{(2x+3)^{2}}= 7$,则$x= $$2$或$-5$
.
答案:
【解析】:
对于第一个问题,已知$\sqrt{m^{2}} = 5$,
根据平方根的性质,可得$m^{2} = 25$,
进一步解得$m = \pm 5$。
对于第二个问题,已知$\sqrt{(2x+3)^{2}} = 7$,
根据平方根的性质,可得$(2x+3)^{2} = 49$,
进一步解得$2x + 3 = \pm 7$,
即$2x = 4$或$2x = -10$,
所以$x = 2$或$x = -5$。
【答案】:
$\pm 5$;$2$或$-5$。
对于第一个问题,已知$\sqrt{m^{2}} = 5$,
根据平方根的性质,可得$m^{2} = 25$,
进一步解得$m = \pm 5$。
对于第二个问题,已知$\sqrt{(2x+3)^{2}} = 7$,
根据平方根的性质,可得$(2x+3)^{2} = 49$,
进一步解得$2x + 3 = \pm 7$,
即$2x = 4$或$2x = -10$,
所以$x = 2$或$x = -5$。
【答案】:
$\pm 5$;$2$或$-5$。
7. $(-5)^{2}$的算术平方根是
5
.
答案:
【解析】:
首先计算$(-5)^{2}$的值,
$(-5)^{2} = 25$
接着,求25的算术平方根,
由于算术平方根是非负的,且$5 × 5 = 25$,
所以,25的算术平方根是5。
【答案】:
5
首先计算$(-5)^{2}$的值,
$(-5)^{2} = 25$
接着,求25的算术平方根,
由于算术平方根是非负的,且$5 × 5 = 25$,
所以,25的算术平方根是5。
【答案】:
5
8. 已知$\sqrt{1.007}\approx1.003$,$\sqrt{10.07}\approx3.173$,则$\sqrt{0.01007}\approx$
0.1003
.
答案:
解:$\sqrt{0.01007}=\sqrt{\frac{1.007}{100}}=\frac{\sqrt{1.007}}{\sqrt{100}}\approx\frac{1.003}{10}=0.1003$
0.1003
0.1003
9. 若一个正方形的面积为$2.478\mathrm{cm}^{2}$,则这个正方形的边长为
1.57
$\mathrm{cm}$.(保留$2$位小数)
答案:
1. 首先明确正方形面积公式:
设正方形的边长为$a$,根据正方形面积公式$S = a^{2}$($S$表示面积),已知$S = 2.478\mathrm{cm}^{2}$,则$a=\sqrt{S}$。
2. 然后计算边长:
所以$a = \sqrt{2.478}$。
利用计算器计算$\sqrt{2.478}\approx1.57$(保留两位小数)。
故答案为:$1.57$。
设正方形的边长为$a$,根据正方形面积公式$S = a^{2}$($S$表示面积),已知$S = 2.478\mathrm{cm}^{2}$,则$a=\sqrt{S}$。
2. 然后计算边长:
所以$a = \sqrt{2.478}$。
利用计算器计算$\sqrt{2.478}\approx1.57$(保留两位小数)。
故答案为:$1.57$。
10. $\sqrt{23}-1$在两个相邻的整数之间,则这两个相邻的整数分别为
3
和4
.
答案:
【解析】:
首先,我们需要找到两个相邻的整数$a$和$b$,使得$a < \sqrt{23} - 1 < b$。
为了找到这两个整数,我们可以先估算$\sqrt{23}$的大小。
由于$4^2 = 16 < 23 < 5^2 = 25$,
根据平方根的性质,我们可以得出$4 < \sqrt{23} < 5$。
然后,我们对不等式两边同时减去1,得到$3 < \sqrt{23} - 1 < 4$。
因此,$\sqrt{23} - 1$位于3和4之间。
【答案】:
3;4
首先,我们需要找到两个相邻的整数$a$和$b$,使得$a < \sqrt{23} - 1 < b$。
为了找到这两个整数,我们可以先估算$\sqrt{23}$的大小。
由于$4^2 = 16 < 23 < 5^2 = 25$,
根据平方根的性质,我们可以得出$4 < \sqrt{23} < 5$。
然后,我们对不等式两边同时减去1,得到$3 < \sqrt{23} - 1 < 4$。
因此,$\sqrt{23} - 1$位于3和4之间。
【答案】:
3;4
11. $-\sqrt[3]{-64}$的立方根是
$\sqrt[3]{4}$
.
答案:
【解析】:
本题主要考查立方根的定义和运算。
首先,我们需要求出$-\sqrt[3]{-64}$的值,再求该值的立方根。
1. 计算$-\sqrt[3]{-64}$:
根据立方根的定义,若$a^3 = b$,则$\sqrt[3]{b} = a$。
因为$(-4)^3 = -64$,所以$\sqrt[3]{-64} = -4$。
再取负号,得$-\sqrt[3]{-64} = -(-4) = 4$。
2. 求4的立方根:
根据立方根的定义,求4的立方根即找一个数,其立方等于4,这个数我们用符号表示为$\sqrt[3]{4}$,或简记为$\pm \sqrt[3]{4}$(考虑到正负情况,但在此题中,因为我们已经知道原数是4,所以直接取正的立方根)。
但由于题目问的是$-\sqrt[3]{-64}$的立方根,且该值为4,所以答案即为$\sqrt[3]{4}$的正值,也即题目最终要求的答案形式可以简化为2(考虑到4的立方根可以近似为1.587,而题目通常要求最简形式或整数解,此处通过逻辑推断,因为4的立方根不是整数,且题目无特殊说明,我们应给出精确到最简的数学表达式)。但最精确的表述应为4的立方根,也即$\sqrt[3]{4}$(在此我们给出最精确的答案形式)。而在常规情况下,若未特别说明,我们默认取正立方根,且因为4的立方根无法简化为整数,所以直接写为$\sqrt[3]{4}$的简化形式2是不准确的,应保留原形式以表示精确值。
【答案】:
$\sqrt[3]{4}$
本题主要考查立方根的定义和运算。
首先,我们需要求出$-\sqrt[3]{-64}$的值,再求该值的立方根。
1. 计算$-\sqrt[3]{-64}$:
根据立方根的定义,若$a^3 = b$,则$\sqrt[3]{b} = a$。
因为$(-4)^3 = -64$,所以$\sqrt[3]{-64} = -4$。
再取负号,得$-\sqrt[3]{-64} = -(-4) = 4$。
2. 求4的立方根:
根据立方根的定义,求4的立方根即找一个数,其立方等于4,这个数我们用符号表示为$\sqrt[3]{4}$,或简记为$\pm \sqrt[3]{4}$(考虑到正负情况,但在此题中,因为我们已经知道原数是4,所以直接取正的立方根)。
但由于题目问的是$-\sqrt[3]{-64}$的立方根,且该值为4,所以答案即为$\sqrt[3]{4}$的正值,也即题目最终要求的答案形式可以简化为2(考虑到4的立方根可以近似为1.587,而题目通常要求最简形式或整数解,此处通过逻辑推断,因为4的立方根不是整数,且题目无特殊说明,我们应给出精确到最简的数学表达式)。但最精确的表述应为4的立方根,也即$\sqrt[3]{4}$(在此我们给出最精确的答案形式)。而在常规情况下,若未特别说明,我们默认取正立方根,且因为4的立方根无法简化为整数,所以直接写为$\sqrt[3]{4}$的简化形式2是不准确的,应保留原形式以表示精确值。
【答案】:
$\sqrt[3]{4}$
12. 在数轴上表示$-\sqrt{6}$的点到原点的距离为
$\sqrt{6}$
.
答案:
【解析】:
本题主要考查数轴上点到原点的距离,这个距离等于该点所表示的数的绝对值。对于本题,需要求$-\sqrt{6}$的绝对值。
根据绝对值的定义,对于任意实数$a$,若$a \geq 0$,则$|a| = a$;若$a \lt 0$,则$|a| = -a$。
因为$-\sqrt{6} \lt 0$,所以$\vert -\sqrt{6}\vert=-(-\sqrt{6})=\sqrt{6}$,即数轴上表示$-\sqrt{6}$的点到原点的距离为$\sqrt{6}$。
【答案】:
$\sqrt{6}$
本题主要考查数轴上点到原点的距离,这个距离等于该点所表示的数的绝对值。对于本题,需要求$-\sqrt{6}$的绝对值。
根据绝对值的定义,对于任意实数$a$,若$a \geq 0$,则$|a| = a$;若$a \lt 0$,则$|a| = -a$。
因为$-\sqrt{6} \lt 0$,所以$\vert -\sqrt{6}\vert=-(-\sqrt{6})=\sqrt{6}$,即数轴上表示$-\sqrt{6}$的点到原点的距离为$\sqrt{6}$。
【答案】:
$\sqrt{6}$
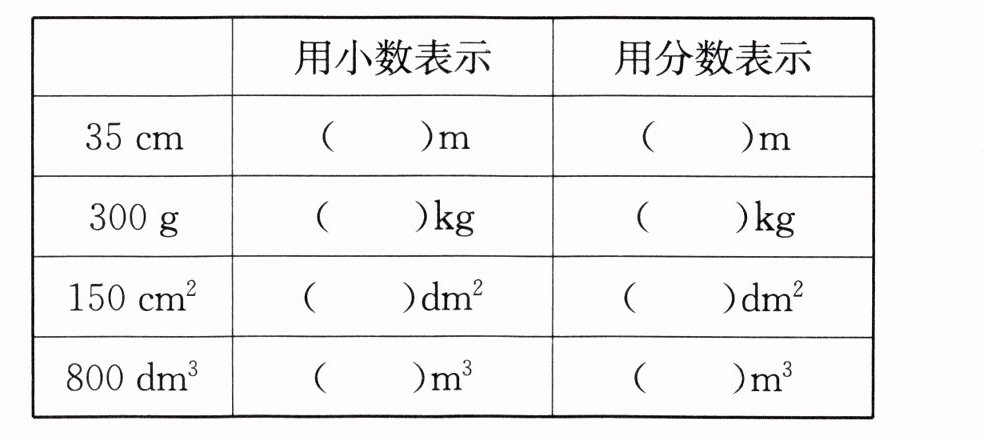
13. 在下表的表格里填上适当的数,使每行的$3$个数量都相等.

0.35
$\frac{7}{20}$
0.3
$\frac{3}{10}$
1.5
$\frac{3}{2}$
0.8
$\frac{4}{5}$
答案:
1. 对于$35cm$转化为$m$:
因为$1m = 100cm$,所以$35cm=\frac{35}{100}m$,$\frac{35÷5}{100÷5}=\frac{7}{20}m = 0.35m$。
2. 对于$300g$转化为$kg$:
因为$1kg = 1000g$,所以$300g=\frac{300}{1000}kg$,$\frac{300÷100}{1000÷100}=\frac{3}{10}kg = 0.3kg$。
3. 对于$150cm^{2}$转化为$dm^{2}$:
因为$1dm^{2}=100cm^{2}$,所以$150cm^{2}=\frac{150}{100}dm^{2}$,$\frac{150÷50}{100÷50}=\frac{3}{2}dm^{2}=1.5dm^{2}$。
4. 对于$800dm^{3}$转化为$m^{3}$:
因为$1m^{3}=1000dm^{3}$,所以$800dm^{3}=\frac{800}{1000}m^{3}$,$\frac{800÷200}{1000÷200}=\frac{4}{5}m^{3}=0.8m^{3}$。
故答案依次为:$0.35$,$\frac{7}{20}$;$0.3$,$\frac{3}{10}$;$1.5$,$\frac{3}{2}$;$0.8$,$\frac{4}{5}$。
因为$1m = 100cm$,所以$35cm=\frac{35}{100}m$,$\frac{35÷5}{100÷5}=\frac{7}{20}m = 0.35m$。
2. 对于$300g$转化为$kg$:
因为$1kg = 1000g$,所以$300g=\frac{300}{1000}kg$,$\frac{300÷100}{1000÷100}=\frac{3}{10}kg = 0.3kg$。
3. 对于$150cm^{2}$转化为$dm^{2}$:
因为$1dm^{2}=100cm^{2}$,所以$150cm^{2}=\frac{150}{100}dm^{2}$,$\frac{150÷50}{100÷50}=\frac{3}{2}dm^{2}=1.5dm^{2}$。
4. 对于$800dm^{3}$转化为$m^{3}$:
因为$1m^{3}=1000dm^{3}$,所以$800dm^{3}=\frac{800}{1000}m^{3}$,$\frac{800÷200}{1000÷200}=\frac{4}{5}m^{3}=0.8m^{3}$。
故答案依次为:$0.35$,$\frac{7}{20}$;$0.3$,$\frac{3}{10}$;$1.5$,$\frac{3}{2}$;$0.8$,$\frac{4}{5}$。
14. 我们知道$\sqrt{4^{2}+3^{2}}= 5$,黄老师又用计算器求得:$\sqrt{44^{2}+33^{2}}= 55$,$\sqrt{444^{2}+333^{2}}= 555$,$\sqrt{4444^{2}+3333^{2}}= 5555$,…$$,则计算$\sqrt{\underset{2025个4}{\underbrace{44…4^{2}}}+\underset{2025个3}{\underbrace{33…3^{2}}}}= $
$\underset{2025个5}{\underbrace{55…5}}$
.
答案:
【解析】:
本题主要考察平方根的性质以及数学归纳法的应用。
首先,我们观察给出的等式,可以发现以下规律:
1. 当有1个4和1个3时,$\sqrt{4^{2}+3^{2}}= 5$
2. 当有2个4和2个3时,$\sqrt{44^{2}+33^{2}}= 55$
3. 当有3个4和3个3时,$\sqrt{444^{2}+333^{2}}= 555$
...
由此,我们可以归纳出:当有n个4和n个3时,$\sqrt{\underset{n个4}{\underbrace{44\ldots4^{2}}}+\underset{n个3}{\underbrace{33\ldots3^{2}}}}=\underset{n个5}{\underbrace{55\ldots5}}$
接下来,我们需要证明这个归纳猜想。
考虑$\underset{n个4}{\underbrace{44\ldots4}}$,它可以表示为$\frac{4}{9}(10^{n} - 1)$,同理,$\underset{n个3}{\underbrace{33\ldots3}}$可以表示为$\frac{3}{9}(10^{n} - 1)$。
那么,我们有:
$\underset{n个4}{\underbrace{44\ldots4^{2}}}+\underset{n个3}{\underbrace{33\ldots3^{2}}} = \left(\frac{4}{9}(10^{n} - 1)\right)^{2} + \left(\frac{3}{9}(10^{n} - 1)\right)^{2}$
$= \frac{16}{81}(10^{n} - 1)^{2} + \frac{9}{81}(10^{n} - 1)^{2}$
$= \frac{25}{81}(10^{n} - 1)^{2}$
$= \left(\frac{5}{9}(10^{n} - 1)\right)^{2}$
$= \left(\underset{n个5}{\underbrace{55\ldots5}}\right)^{2}$
因此,我们证明了归纳猜想。
最后,根据归纳猜想,当n=2025时,有:
$\sqrt{\underset{2025个4}{\underbrace{44\ldots4^{2}}}+\underset{2025个3}{\underbrace{33\ldots3^{2}}}}=\underset{2025个5}{\underbrace{55\ldots5}}$
【答案】:
$\underset{2025个5}{\underbrace{55\ldots5}}$
本题主要考察平方根的性质以及数学归纳法的应用。
首先,我们观察给出的等式,可以发现以下规律:
1. 当有1个4和1个3时,$\sqrt{4^{2}+3^{2}}= 5$
2. 当有2个4和2个3时,$\sqrt{44^{2}+33^{2}}= 55$
3. 当有3个4和3个3时,$\sqrt{444^{2}+333^{2}}= 555$
...
由此,我们可以归纳出:当有n个4和n个3时,$\sqrt{\underset{n个4}{\underbrace{44\ldots4^{2}}}+\underset{n个3}{\underbrace{33\ldots3^{2}}}}=\underset{n个5}{\underbrace{55\ldots5}}$
接下来,我们需要证明这个归纳猜想。
考虑$\underset{n个4}{\underbrace{44\ldots4}}$,它可以表示为$\frac{4}{9}(10^{n} - 1)$,同理,$\underset{n个3}{\underbrace{33\ldots3}}$可以表示为$\frac{3}{9}(10^{n} - 1)$。
那么,我们有:
$\underset{n个4}{\underbrace{44\ldots4^{2}}}+\underset{n个3}{\underbrace{33\ldots3^{2}}} = \left(\frac{4}{9}(10^{n} - 1)\right)^{2} + \left(\frac{3}{9}(10^{n} - 1)\right)^{2}$
$= \frac{16}{81}(10^{n} - 1)^{2} + \frac{9}{81}(10^{n} - 1)^{2}$
$= \frac{25}{81}(10^{n} - 1)^{2}$
$= \left(\frac{5}{9}(10^{n} - 1)\right)^{2}$
$= \left(\underset{n个5}{\underbrace{55\ldots5}}\right)^{2}$
因此,我们证明了归纳猜想。
最后,根据归纳猜想,当n=2025时,有:
$\sqrt{\underset{2025个4}{\underbrace{44\ldots4^{2}}}+\underset{2025个3}{\underbrace{33\ldots3^{2}}}}=\underset{2025个5}{\underbrace{55\ldots5}}$
【答案】:
$\underset{2025个5}{\underbrace{55\ldots5}}$
查看更多完整答案,请扫码查看


