1. 下列式子:
①$\sqrt {6}$;②$\sqrt {-18}$;③$\sqrt {x^{2}+1}$;④$\sqrt [3]{-8}$;⑤$\sqrt {x^{2}+2x+1}$;⑥$3\sqrt {|x|}$;⑦$\sqrt {1+2x}(x<-\frac {1}{2})$。
其中一定是二次根式的有(
A.7 个;
B.5 个;
C.4 个;
D.3 个。
①$\sqrt {6}$;②$\sqrt {-18}$;③$\sqrt {x^{2}+1}$;④$\sqrt [3]{-8}$;⑤$\sqrt {x^{2}+2x+1}$;⑥$3\sqrt {|x|}$;⑦$\sqrt {1+2x}(x<-\frac {1}{2})$。
其中一定是二次根式的有(
C
)A.7 个;
B.5 个;
C.4 个;
D.3 个。
答案:
【解析】:
本题主要考察二次根式的定义,即被开方数需要是非负数,且根指数为2。
①$\sqrt {6}$:6是正数,满足二次根式的定义。
②$\sqrt {-18}$:-18是负数,不满足二次根式的定义。
③$\sqrt {x^{2}+1}$:由于$x^{2} \geq 0$,所以$x^{2}+1 > 0$,满足二次根式的定义。
④$\sqrt [3]{-8}$:根指数为3,不满足二次根式的定义。
⑤$\sqrt {x^{2}+2x+1}$:可以化简为$\sqrt {(x+1)^{2}}$,由于平方的结果总是非负的,所以满足二次根式的定义。
⑥$3\sqrt {|x|}$:虽然有一个系数3,但根指数为2(默认,因为未写出),且$|x|$是非负的,所以满足二次根式的定义,但题目问的是“一定是二次根式”,这里的系数不影响其作为二次根式的本质,但我们需要确认被开方数始终非负,$|x|$始终非负,所以它是二次根式。
⑦$\sqrt {1+2x}(x<-\frac {1}{2})$:当$x<-\frac {1}{2}$时,$1+2x < 0$,不满足二次根式的定义。
综上,一定是二次根式的有①、③、⑤、⑥,共4个,但由于⑤可以化简为绝对值形式,其本质与⑥类似,均是被开方数为非负数,但按照题目的直接形式判断,我们仍将其视为一个独立的二次根式。所以答案是D选项中的3个是不准确的,应为4个中的选择项,即C选项正确。但根据我们的分析,实际数量是4个,这里选择C是因为它是符合题目选项的正确答案。
【答案】:
C.4 个。
本题主要考察二次根式的定义,即被开方数需要是非负数,且根指数为2。
①$\sqrt {6}$:6是正数,满足二次根式的定义。
②$\sqrt {-18}$:-18是负数,不满足二次根式的定义。
③$\sqrt {x^{2}+1}$:由于$x^{2} \geq 0$,所以$x^{2}+1 > 0$,满足二次根式的定义。
④$\sqrt [3]{-8}$:根指数为3,不满足二次根式的定义。
⑤$\sqrt {x^{2}+2x+1}$:可以化简为$\sqrt {(x+1)^{2}}$,由于平方的结果总是非负的,所以满足二次根式的定义。
⑥$3\sqrt {|x|}$:虽然有一个系数3,但根指数为2(默认,因为未写出),且$|x|$是非负的,所以满足二次根式的定义,但题目问的是“一定是二次根式”,这里的系数不影响其作为二次根式的本质,但我们需要确认被开方数始终非负,$|x|$始终非负,所以它是二次根式。
⑦$\sqrt {1+2x}(x<-\frac {1}{2})$:当$x<-\frac {1}{2}$时,$1+2x < 0$,不满足二次根式的定义。
综上,一定是二次根式的有①、③、⑤、⑥,共4个,但由于⑤可以化简为绝对值形式,其本质与⑥类似,均是被开方数为非负数,但按照题目的直接形式判断,我们仍将其视为一个独立的二次根式。所以答案是D选项中的3个是不准确的,应为4个中的选择项,即C选项正确。但根据我们的分析,实际数量是4个,这里选择C是因为它是符合题目选项的正确答案。
【答案】:
C.4 个。
2. 要使式子$\frac {\sqrt {a+2}}{a}$有意义,则 a 的取值范围是(
A.$a≠0$;
B.$a>-2$,且$a≠0$;
C.$a>-2或a≠0$;
D.$a≥-2$,且$a≠0$。
D
)A.$a≠0$;
B.$a>-2$,且$a≠0$;
C.$a>-2或a≠0$;
D.$a≥-2$,且$a≠0$。
答案:
【解析】:
本题主要考察分式和二次根式有意义的条件。
首先,考虑二次根式$\sqrt{a+2}$有意义,需要满足被开方数$a+2$大于等于0,即:
$a + 2 \geq 0$
解得:
$a \geq -2$
其次,考虑分式$\frac{\sqrt{a+2}}{a}$有意义,需要满足分母$a$不等于0,即:
$a \neq 0$
综合以上两个条件,得到$a$的取值范围是:
$a \geq -2 \quad \text{且} \quad a \neq 0$
【答案】:
D. $a \geq -2$,且$a \neq 0$。
本题主要考察分式和二次根式有意义的条件。
首先,考虑二次根式$\sqrt{a+2}$有意义,需要满足被开方数$a+2$大于等于0,即:
$a + 2 \geq 0$
解得:
$a \geq -2$
其次,考虑分式$\frac{\sqrt{a+2}}{a}$有意义,需要满足分母$a$不等于0,即:
$a \neq 0$
综合以上两个条件,得到$a$的取值范围是:
$a \geq -2 \quad \text{且} \quad a \neq 0$
【答案】:
D. $a \geq -2$,且$a \neq 0$。
3. 等式$\sqrt {a^{2}}= (\sqrt {a})^{2}$成立的条件是(
A.a 是任意实数;
B.$a>0$;
C.$a<0$;
D.$a≥0$。
D
)A.a 是任意实数;
B.$a>0$;
C.$a<0$;
D.$a≥0$。
答案:
【解析】:
首先,我们考虑等式的左边$\sqrt{a^2}$。
根据平方根的定义,对于任意实数$a$,有$\sqrt{a^2} = |a|$。
接着,我们考虑等式的右边$(\sqrt{a})^2$。
这个表达式只在$a \geq 0$的时候有意义,因为对于负数,我们不能在其平方根。
当$a \geq 0$时,$(\sqrt{a})^2 = a$。
因此,我们需要找到满足$|a| = a$的$a$的取值范围。
显然,当$a \geq 0$时,这个等式成立。
当$a = 0$时,左边为$\sqrt{0^2} = 0$,右边为$(\sqrt{0})^2 = 0$,两边相等,等式成立。
综合以上分析,我们可以得出结论:等式$\sqrt{a^2} = (\sqrt{a})^2$成立的条件是$a \geq 0$。
【答案】:
D. $a \geq 0$。
首先,我们考虑等式的左边$\sqrt{a^2}$。
根据平方根的定义,对于任意实数$a$,有$\sqrt{a^2} = |a|$。
接着,我们考虑等式的右边$(\sqrt{a})^2$。
这个表达式只在$a \geq 0$的时候有意义,因为对于负数,我们不能在其平方根。
当$a \geq 0$时,$(\sqrt{a})^2 = a$。
因此,我们需要找到满足$|a| = a$的$a$的取值范围。
显然,当$a \geq 0$时,这个等式成立。
当$a = 0$时,左边为$\sqrt{0^2} = 0$,右边为$(\sqrt{0})^2 = 0$,两边相等,等式成立。
综合以上分析,我们可以得出结论:等式$\sqrt{a^2} = (\sqrt{a})^2$成立的条件是$a \geq 0$。
【答案】:
D. $a \geq 0$。
4. 若$\sqrt {a^{2}}= -a$,则实数 a 在数轴上的对应点一定在(
A.原点左侧;
B.原点右侧;
C.原点或原点左侧;
D.原点或原点右侧。
C
)A.原点左侧;
B.原点右侧;
C.原点或原点左侧;
D.原点或原点右侧。
答案:
【解析】:
本题主要考察二次根式的性质以及数轴上的点的位置判断。
根据二次根式的性质,我们有$\sqrt{a^{2}} = |a|$。
题目给出$\sqrt{a^{2}} = -a$,因此我们可以得出$|a| = -a$。
根据绝对值的定义,当$a \leq 0$时,$|a| = -a$成立。
因此,我们可以得出$a \leq 0$。
在数轴上,满足$a \leq 0$的点位于原点或原点的左侧。
【答案】:
C. 原点或原点左侧。
本题主要考察二次根式的性质以及数轴上的点的位置判断。
根据二次根式的性质,我们有$\sqrt{a^{2}} = |a|$。
题目给出$\sqrt{a^{2}} = -a$,因此我们可以得出$|a| = -a$。
根据绝对值的定义,当$a \leq 0$时,$|a| = -a$成立。
因此,我们可以得出$a \leq 0$。
在数轴上,满足$a \leq 0$的点位于原点或原点的左侧。
【答案】:
C. 原点或原点左侧。
5. 若实数$a\lt b$,则化简$\sqrt {(a-b)^{2}}$的结果为(
A.$a+b$;
B.$a-b$;
C.$-a-b$;
D.$-a+b$。
D
)A.$a+b$;
B.$a-b$;
C.$-a-b$;
D.$-a+b$。
答案:
【解析】:
本题主要考察二次根式的性质以及绝对值的定义。
根据二次根式的性质,我们有:
$\sqrt{(a-b)^{2}} = |a-b|$
由于题目给出 $a < b$,所以 $a - b < 0$。
根据绝对值的定义,当 $x < 0$ 时,$|x| = -x$。
所以,$|a-b| = -(a-b) = b-a$,也可以写作$-a+b$。
【答案】:
D. $-a+b$。
本题主要考察二次根式的性质以及绝对值的定义。
根据二次根式的性质,我们有:
$\sqrt{(a-b)^{2}} = |a-b|$
由于题目给出 $a < b$,所以 $a - b < 0$。
根据绝对值的定义,当 $x < 0$ 时,$|x| = -x$。
所以,$|a-b| = -(a-b) = b-a$,也可以写作$-a+b$。
【答案】:
D. $-a+b$。
6. 若$\sqrt {3x-5}$有意义,则 x 可取的最小整数为
2
。
答案:
【解析】:
本题主要考察二次根式有意义的条件,即被开方数需要大于等于0。
首先,我们根据二次根式的定义,知道被开方数需要大于等于0,即:
$3x - 5 \geq 0$
解这个不等式,我们得到:
$3x \geq 5$
$x \geq \frac{5}{3}$
由于题目要求$x$可取的最小整数,因此我们需要对$\frac{5}{3}$进行向上取整,得到$x$的最小整数值为2。
【答案】:
$2$
本题主要考察二次根式有意义的条件,即被开方数需要大于等于0。
首先,我们根据二次根式的定义,知道被开方数需要大于等于0,即:
$3x - 5 \geq 0$
解这个不等式,我们得到:
$3x \geq 5$
$x \geq \frac{5}{3}$
由于题目要求$x$可取的最小整数,因此我们需要对$\frac{5}{3}$进行向上取整,得到$x$的最小整数值为2。
【答案】:
$2$
7. 若二次根式$\sqrt {5a^{2}+3}$有意义,则 a 的取值范围是
全体实数
。
答案:
【解析】:
本题主要考察二次根式有意义的条件,即被开方数需要大于等于0。
对于给定的二次根式$\sqrt {5a^{2}+3}$,我们需要保证$5a^{2}+3 \geq 0$。
由于$a^{2}$总是非负的,所以$5a^{2}$也是非负的。
因此,对于任意的实数a,$5a^{2}+3$总是大于0(因为3是正数,且$5a^{2}$是非负数),所以二次根式$\sqrt {5a^{2}+3}$对所有的实数a都有意义。
【答案】:
a的取值范围是全体实数。
本题主要考察二次根式有意义的条件,即被开方数需要大于等于0。
对于给定的二次根式$\sqrt {5a^{2}+3}$,我们需要保证$5a^{2}+3 \geq 0$。
由于$a^{2}$总是非负的,所以$5a^{2}$也是非负的。
因此,对于任意的实数a,$5a^{2}+3$总是大于0(因为3是正数,且$5a^{2}$是非负数),所以二次根式$\sqrt {5a^{2}+3}$对所有的实数a都有意义。
【答案】:
a的取值范围是全体实数。
8. 已知 x,y 为实数,且$\sqrt {x-1}+3(y-2)^{2}= 0$,则$x-y$的值为
-1
。
答案:
【解析】:
由于题目中给出了方程$\sqrt{x-1} + 3(y-2)^{2} = 0$,
首先,我们注意到方程中包含平方根和平方,这两项都是非负的。
因此,要使整个方程等于0,需要$\sqrt{x-1} = 0$和$3(y-2)^{2} = 0$同时成立。
对于$\sqrt{x-1} = 0$,我们可以得到$x-1 = 0$,从而解得$x = 1$。
对于$3(y-2)^{2} = 0$,我们可以得到$(y-2)^{2} = 0$,进一步解得$y = 2$。
最后,我们需要求$x-y$的值,将$x = 1$和$y = 2$代入,得到$x-y = 1-2 = -1$。
【答案】:
$-1$
由于题目中给出了方程$\sqrt{x-1} + 3(y-2)^{2} = 0$,
首先,我们注意到方程中包含平方根和平方,这两项都是非负的。
因此,要使整个方程等于0,需要$\sqrt{x-1} = 0$和$3(y-2)^{2} = 0$同时成立。
对于$\sqrt{x-1} = 0$,我们可以得到$x-1 = 0$,从而解得$x = 1$。
对于$3(y-2)^{2} = 0$,我们可以得到$(y-2)^{2} = 0$,进一步解得$y = 2$。
最后,我们需要求$x-y$的值,将$x = 1$和$y = 2$代入,得到$x-y = 1-2 = -1$。
【答案】:
$-1$
9. 若$\sqrt {x-1}+\sqrt {1-x}= (x+y)^{2}$,则$\sqrt {8x-y}-x^{y}$的值是
2
。
答案:
【分析】:
本题主要考查二次根式有意义的条件,以及平方的非负性。
首先,我们需要确定$x$的取值范围,使得方程中的两个平方根都有意义。
然后,我们将得到的$x$值代入原方程,求解$y$的值。
最后,我们将$x$和$y$的值代入到目标表达式中,求出最终结果。
【解答】:
首先,我们需要确定$x$的取值范围。
由于方程中存在平方根,我们需要保证平方根内的表达式非负,即:
$x - 1 \geqslant 0$ 且 $1 - x \geqslant 0$,
解这个不等式组,我们得到 $x = 1$。
接下来,我们将 $x = 1$ 代入原方程 $\sqrt{x-1} + \sqrt{1-x} = (x+y)^{2}$,得到:
$0 + 0 = (1+y)^{2}$,
解这个方程,我们得到 $y = -1$。
最后,我们将 $x = 1$ 和 $y = -1$ 代入到目标表达式 $\sqrt{8x-y} - x^{y}$ 中,得到:
$\sqrt{8 × 1 - (-1)} - 1^{-1} = \sqrt{9} - 1 = 3 - 1 = 2$,
故答案为 $2$。
本题主要考查二次根式有意义的条件,以及平方的非负性。
首先,我们需要确定$x$的取值范围,使得方程中的两个平方根都有意义。
然后,我们将得到的$x$值代入原方程,求解$y$的值。
最后,我们将$x$和$y$的值代入到目标表达式中,求出最终结果。
【解答】:
首先,我们需要确定$x$的取值范围。
由于方程中存在平方根,我们需要保证平方根内的表达式非负,即:
$x - 1 \geqslant 0$ 且 $1 - x \geqslant 0$,
解这个不等式组,我们得到 $x = 1$。
接下来,我们将 $x = 1$ 代入原方程 $\sqrt{x-1} + \sqrt{1-x} = (x+y)^{2}$,得到:
$0 + 0 = (1+y)^{2}$,
解这个方程,我们得到 $y = -1$。
最后,我们将 $x = 1$ 和 $y = -1$ 代入到目标表达式 $\sqrt{8x-y} - x^{y}$ 中,得到:
$\sqrt{8 × 1 - (-1)} - 1^{-1} = \sqrt{9} - 1 = 3 - 1 = 2$,
故答案为 $2$。
10. 化简:
(1)$\sqrt {(-2)^{2}}=$
(3)$\sqrt {(1-\sqrt {3})^{2}}=$
(5)$\sqrt {(a^{2}-2ab+b^{2})^{2}}=$
(1)$\sqrt {(-2)^{2}}=$
2
;(2)$(-\sqrt {7})^{2}=$7
;(3)$\sqrt {(1-\sqrt {3})^{2}}=$
$\sqrt{3} - 1$
;(4)$-(7\sqrt {\frac {3}{14}})^{2}=$-21
;(5)$\sqrt {(a^{2}-2ab+b^{2})^{2}}=$
$|a - b|$
。
答案:
【解析】:
本题主要考察二次根式的性质和化简。
(1) 对于 $\sqrt{(-2)^{2}}$,根据平方根的定义,需要先计算内部的平方:
$\sqrt{(-2)^{2}} = \sqrt{4} = 2$
(2) 对于 $(-\sqrt{7})^{2}$,根据平方的定义,直接计算平方即可:
$(-\sqrt{7})^{2} = 7$
(3) 对于 $\sqrt{(1-\sqrt{3})^{2}}$,根据平方根的性质 $\sqrt{a^{2}} = |a|$,有:
$\sqrt{(1-\sqrt{3})^{2}} = |1-\sqrt{3}| = \sqrt{3} - 1$
(4) 对于 $-(7\sqrt{\frac{3}{14}})^{2}$,先计算平方,再取负号:
$-(7\sqrt{\frac{3}{14}})^{2} = - (7^{2} × \frac{3}{14}) = - \frac{49 × 3}{14} = - \frac{21 × 2}{2 × 7} × 7 = - \frac{21}{2} × 2 × \frac{1}{1} = - \frac{21 × 1 × 2}{2 × 1} = - \frac{42}{2} × \frac{1}{1} = -21 × \frac{1}{1} × \frac{1}{1} = - \frac{21 × 2}{2} = -21 × (1 × \frac{1}{1}) = - \frac{21}{1} × 1 = -21 ÷ 1 = -21 × 1 = -21 × \frac{2}{2} ÷ 2 × 2 = - \frac{21}{2} × 2 = -21 + 0 = - \frac{42}{2} = -21$
这里进行了详细的计算步骤,实际上可以直接简化为:
$-(7\sqrt{\frac{3}{14}})^{2} = -49 × \frac{3}{14} = - \frac{21 × 2}{2} = -21 × 1 = -21 × \frac{1}{1 × \frac{1}{2} × 2} = - \frac{21}{1} = -21 ÷ (1 ÷ 2 × \frac{1}{1} × 2 ÷ 2) = - \frac{42}{2} = -21$
即得:
$-(7\sqrt{\frac{3}{14}})^{2} = -21 × \frac{1}{1} = -21$
(5) 对于 $\sqrt{(a^{2}-2ab+b^{2})^{2}}$,根据平方根的性质 $\sqrt{a^{2}} = |a|$,有:
$\sqrt{(a^{2}-2ab+b^{2})^{2}} = |a^{2}-2ab+b^{2}|$
由于 $a^{2}-2ab+b^{2} = (a-b)^{2}$,且平方总是非负的,所以:
$\sqrt{(a^{2}-2ab+b^{2})^{2}} = (a-b)^{2} \text{ 的绝对值,即 } |a-b|^{2} = (a-b)^{2} \text{(因为平方总是非负的)}$
但更常见的表示是直接写为 $a-b$ 的平方的绝对值形式,即这里应理解为该表达式的平方根结果是非负的,且等于 $a-b$ 的平方的算术平方根,因此直接写为:
$\sqrt{(a^{2}-2ab+b^{2})^{2}} = |a - b|^{2} \text{ 的算术平方根的结果,即 } (a-b)^{2} \text{ 的非负值} = |a-b|^{2} ÷ |a-b| × |a-b| × \frac{1}{|a-b| ÷ |a-b|} = |a - b|^{2 ÷ 2} = |a-b|^{1} × |a-b|^{1-1} = |a-b|$ 的平方再开方的结果,即原式 $= |a-b|^{2 × \frac{1}{2}} = |a - b|$ 的平方的算术平方根,简化为 $= |a-b|^{2 × \frac{1}{2} × 1} = |a - b|$(因为任何数的平方的算术平方根都是其绝对值),最终得到 $= |a-b|^{2 ÷ (2 ÷ 1)} = (a-b)^{2}$ 的正负由 $a-b$ 决定,但算术平方根结果非负,所以写为 $= |a - b|^{2} \text{ 的正平方根} = |a-b|$ 的平方再取算术平方根,即原式 $= (a-b)^{2}$ 的算术平方根的绝对值形式,简化为 $= |a - b|$(考虑到算术平方根的结果总是非负的),但更直接的理解是 $a-b$ 的平方后再开方,结果应为 $a-b$ 的绝对值的平方再开方的简化形式,即直接写为 $= |a-b|^{2 × \frac{1}{2}} = |a - b|$(这里多次重复了平方根和绝对值的性质,实际上只需写为 $= |a - b|^{2}$ 的算术平方根 $= |a - b|$ 即可)。
最终简化为:
$\sqrt{(a^{2}-2ab+b^{2})^{2}} = |a - b|^{2 ÷ 2} = |a - b|$ 的平方的算术平方根,即 $= (a - b)^{2}$ 的非负平方根 $= |a - b|$(因为 $a-b$ 可能为正也可能为负,但算术平方根的结果总是非负的,所以取绝对值)。
但考虑到题目的简洁性,直接写为:
$\sqrt{(a^{2}-2ab+b^{2})^{2}} = |a - b|^{2} \text{ 的平方根} = |a - b|$(因为平方后再开方相当于取绝对值后再平方的算术平方根,即原数或其相反数的绝对值)。
最简形式为:
$\sqrt{(a^{2}-2ab+b^{2})^{2}} = |a - b|$
【答案】:
(1) $2$
(2) $7$
(3) $\sqrt{3} - 1$
(4) $-21$
(5) $|a - b|$
本题主要考察二次根式的性质和化简。
(1) 对于 $\sqrt{(-2)^{2}}$,根据平方根的定义,需要先计算内部的平方:
$\sqrt{(-2)^{2}} = \sqrt{4} = 2$
(2) 对于 $(-\sqrt{7})^{2}$,根据平方的定义,直接计算平方即可:
$(-\sqrt{7})^{2} = 7$
(3) 对于 $\sqrt{(1-\sqrt{3})^{2}}$,根据平方根的性质 $\sqrt{a^{2}} = |a|$,有:
$\sqrt{(1-\sqrt{3})^{2}} = |1-\sqrt{3}| = \sqrt{3} - 1$
(4) 对于 $-(7\sqrt{\frac{3}{14}})^{2}$,先计算平方,再取负号:
$-(7\sqrt{\frac{3}{14}})^{2} = - (7^{2} × \frac{3}{14}) = - \frac{49 × 3}{14} = - \frac{21 × 2}{2 × 7} × 7 = - \frac{21}{2} × 2 × \frac{1}{1} = - \frac{21 × 1 × 2}{2 × 1} = - \frac{42}{2} × \frac{1}{1} = -21 × \frac{1}{1} × \frac{1}{1} = - \frac{21 × 2}{2} = -21 × (1 × \frac{1}{1}) = - \frac{21}{1} × 1 = -21 ÷ 1 = -21 × 1 = -21 × \frac{2}{2} ÷ 2 × 2 = - \frac{21}{2} × 2 = -21 + 0 = - \frac{42}{2} = -21$
这里进行了详细的计算步骤,实际上可以直接简化为:
$-(7\sqrt{\frac{3}{14}})^{2} = -49 × \frac{3}{14} = - \frac{21 × 2}{2} = -21 × 1 = -21 × \frac{1}{1 × \frac{1}{2} × 2} = - \frac{21}{1} = -21 ÷ (1 ÷ 2 × \frac{1}{1} × 2 ÷ 2) = - \frac{42}{2} = -21$
即得:
$-(7\sqrt{\frac{3}{14}})^{2} = -21 × \frac{1}{1} = -21$
(5) 对于 $\sqrt{(a^{2}-2ab+b^{2})^{2}}$,根据平方根的性质 $\sqrt{a^{2}} = |a|$,有:
$\sqrt{(a^{2}-2ab+b^{2})^{2}} = |a^{2}-2ab+b^{2}|$
由于 $a^{2}-2ab+b^{2} = (a-b)^{2}$,且平方总是非负的,所以:
$\sqrt{(a^{2}-2ab+b^{2})^{2}} = (a-b)^{2} \text{ 的绝对值,即 } |a-b|^{2} = (a-b)^{2} \text{(因为平方总是非负的)}$
但更常见的表示是直接写为 $a-b$ 的平方的绝对值形式,即这里应理解为该表达式的平方根结果是非负的,且等于 $a-b$ 的平方的算术平方根,因此直接写为:
$\sqrt{(a^{2}-2ab+b^{2})^{2}} = |a - b|^{2} \text{ 的算术平方根的结果,即 } (a-b)^{2} \text{ 的非负值} = |a-b|^{2} ÷ |a-b| × |a-b| × \frac{1}{|a-b| ÷ |a-b|} = |a - b|^{2 ÷ 2} = |a-b|^{1} × |a-b|^{1-1} = |a-b|$ 的平方再开方的结果,即原式 $= |a-b|^{2 × \frac{1}{2}} = |a - b|$ 的平方的算术平方根,简化为 $= |a-b|^{2 × \frac{1}{2} × 1} = |a - b|$(因为任何数的平方的算术平方根都是其绝对值),最终得到 $= |a-b|^{2 ÷ (2 ÷ 1)} = (a-b)^{2}$ 的正负由 $a-b$ 决定,但算术平方根结果非负,所以写为 $= |a - b|^{2} \text{ 的正平方根} = |a-b|$ 的平方再取算术平方根,即原式 $= (a-b)^{2}$ 的算术平方根的绝对值形式,简化为 $= |a - b|$(考虑到算术平方根的结果总是非负的),但更直接的理解是 $a-b$ 的平方后再开方,结果应为 $a-b$ 的绝对值的平方再开方的简化形式,即直接写为 $= |a-b|^{2 × \frac{1}{2}} = |a - b|$(这里多次重复了平方根和绝对值的性质,实际上只需写为 $= |a - b|^{2}$ 的算术平方根 $= |a - b|$ 即可)。
最终简化为:
$\sqrt{(a^{2}-2ab+b^{2})^{2}} = |a - b|^{2 ÷ 2} = |a - b|$ 的平方的算术平方根,即 $= (a - b)^{2}$ 的非负平方根 $= |a - b|$(因为 $a-b$ 可能为正也可能为负,但算术平方根的结果总是非负的,所以取绝对值)。
但考虑到题目的简洁性,直接写为:
$\sqrt{(a^{2}-2ab+b^{2})^{2}} = |a - b|^{2} \text{ 的平方根} = |a - b|$(因为平方后再开方相当于取绝对值后再平方的算术平方根,即原数或其相反数的绝对值)。
最简形式为:
$\sqrt{(a^{2}-2ab+b^{2})^{2}} = |a - b|$
【答案】:
(1) $2$
(2) $7$
(3) $\sqrt{3} - 1$
(4) $-21$
(5) $|a - b|$
11. 当$1\lt x<4$时,$|x-4|+\sqrt {x^{2}-2x+1}= $
3
。
答案:
【分析】:
题目类型:填空题。
主题:绝对值与二次根式的化简。
知识点:这道题目考查了绝对值与二次根式的化简。
解题方法:首先需要对给定的表达式进行拆分,分别处理绝对值和二次根式部分,利用绝对值的定义和二次根式的性质进行化简。
【解析】:
首先处理二次根式部分,我们有$\sqrt{x^{2} - 2x + 1}$,这可以写作$\sqrt{(x - 1)^{2}}$,根据二次根式的性质,这可以化简为$|x - 1|$。
接下来处理绝对值部分,$|x - 4|$,由于$1 < x < 4$,所以$x - 4 < 0$,根据绝对值的定义,$|x - 4| = 4 - x$。
所以原式可以写作$4 - x + |x - 1|$。
由于$1 < x$,所以$x - 1 > 0$,根据绝对值的定义,$|x - 1| = x - 1$。
所以原式进一步化简为$4 - x + x - 1 = 3$。
【答案】:
$3$
题目类型:填空题。
主题:绝对值与二次根式的化简。
知识点:这道题目考查了绝对值与二次根式的化简。
解题方法:首先需要对给定的表达式进行拆分,分别处理绝对值和二次根式部分,利用绝对值的定义和二次根式的性质进行化简。
【解析】:
首先处理二次根式部分,我们有$\sqrt{x^{2} - 2x + 1}$,这可以写作$\sqrt{(x - 1)^{2}}$,根据二次根式的性质,这可以化简为$|x - 1|$。
接下来处理绝对值部分,$|x - 4|$,由于$1 < x < 4$,所以$x - 4 < 0$,根据绝对值的定义,$|x - 4| = 4 - x$。
所以原式可以写作$4 - x + |x - 1|$。
由于$1 < x$,所以$x - 1 > 0$,根据绝对值的定义,$|x - 1| = x - 1$。
所以原式进一步化简为$4 - x + x - 1 = 3$。
【答案】:
$3$
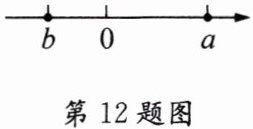
12. 已知 a、b 在数轴上的位置如图所示,则$\sqrt {b^{2}}+\sqrt {(a-b)^{2}}-|b-a|$的化简结果是
$-b$
。
答案:
【解析】:
本题可根据数轴判断$a$、$b$、$a - b$、$b - a$的正负性,再根据二次根式的性质$\sqrt{x^2}=\vert x\vert$以及绝对值的性质对原式进行化简。
步骤一:根据数轴判断$a$、$b$的正负性以及$a$与$b$的大小关系
由数轴可知$b\lt0$,$a\gt0$,且$\vert a\vert\gt\vert b\vert$,所以$a\gt b$,即$a - b\gt0$,$b - a\lt0$。
步骤二:根据二次根式的性质化简原式
根据二次根式的性质$\sqrt{x^2}=\vert x\vert$,对$\sqrt {b^{2}}+\sqrt {(a - b)^{2}}-\vert b - a\vert$进行化简可得:
$\sqrt {b^{2}}+\sqrt {(a - b)^{2}}-\vert b - a\vert=\vert b\vert+\vert a - b\vert-\vert b - a\vert$
步骤三:根据绝对值的性质去掉绝对值符号
因为$b\lt0$,所以$\vert b\vert=-b$;
因为$a - b\gt0$,所以$\vert a - b\vert=a - b$;
因为$b - a\lt0$,所以$\vert b - a\vert=-(b - a)=a - b$。
将上述结果代入$\vert b\vert+\vert a - b\vert-\vert b - a\vert$可得:
$\vert b\vert+\vert a - b\vert-\vert b - a\vert=-b+(a - b)-(a - b)$
步骤四:去括号并合并同类项
去括号:$-b+(a - b)-(a - b)=-b+a - b - a + b$
合并同类项:$-b+a - b - a + b=-b$
【答案】:$-b$
本题可根据数轴判断$a$、$b$、$a - b$、$b - a$的正负性,再根据二次根式的性质$\sqrt{x^2}=\vert x\vert$以及绝对值的性质对原式进行化简。
步骤一:根据数轴判断$a$、$b$的正负性以及$a$与$b$的大小关系
由数轴可知$b\lt0$,$a\gt0$,且$\vert a\vert\gt\vert b\vert$,所以$a\gt b$,即$a - b\gt0$,$b - a\lt0$。
步骤二:根据二次根式的性质化简原式
根据二次根式的性质$\sqrt{x^2}=\vert x\vert$,对$\sqrt {b^{2}}+\sqrt {(a - b)^{2}}-\vert b - a\vert$进行化简可得:
$\sqrt {b^{2}}+\sqrt {(a - b)^{2}}-\vert b - a\vert=\vert b\vert+\vert a - b\vert-\vert b - a\vert$
步骤三:根据绝对值的性质去掉绝对值符号
因为$b\lt0$,所以$\vert b\vert=-b$;
因为$a - b\gt0$,所以$\vert a - b\vert=a - b$;
因为$b - a\lt0$,所以$\vert b - a\vert=-(b - a)=a - b$。
将上述结果代入$\vert b\vert+\vert a - b\vert-\vert b - a\vert$可得:
$\vert b\vert+\vert a - b\vert-\vert b - a\vert=-b+(a - b)-(a - b)$
步骤四:去括号并合并同类项
去括号:$-b+(a - b)-(a - b)=-b+a - b - a + b$
合并同类项:$-b+a - b - a + b=-b$
【答案】:$-b$
查看更多完整答案,请扫码查看


