1. 下列各数是无理数的是 (
A.$π$;
B.$\frac {22}{7}$;
C.$\sqrt {9}$;
D.$\sqrt [5]{32}$.
A
)A.$π$;
B.$\frac {22}{7}$;
C.$\sqrt {9}$;
D.$\sqrt [5]{32}$.
答案:
【解析】:
本题主要考察无理数和有理数的定义及判断。
无理数是不能表示为两个整数的比的数,且其小数部分是无限不循环的。
A选项,$π$是一个无理数,因为它不能表示为两个整数的比,且其小数部分是无限不循环的。
B选项,$\frac{22}{7}$是两个整数的比,所以是有理数。
C选项,$\sqrt{9}=3$,是整数,属于有理数。
D选项,$\sqrt[5]{32}=2$,也是整数,属于有理数。
根据以上分析,只有A选项是无理数。
【答案】:
A
本题主要考察无理数和有理数的定义及判断。
无理数是不能表示为两个整数的比的数,且其小数部分是无限不循环的。
A选项,$π$是一个无理数,因为它不能表示为两个整数的比,且其小数部分是无限不循环的。
B选项,$\frac{22}{7}$是两个整数的比,所以是有理数。
C选项,$\sqrt{9}=3$,是整数,属于有理数。
D选项,$\sqrt[5]{32}=2$,也是整数,属于有理数。
根据以上分析,只有A选项是无理数。
【答案】:
A
2. $-8$的立方根是 (
A.$2\sqrt {2}$;
B.2;
C.$-2$;
D.$-2\sqrt {2}$.
C
)A.$2\sqrt {2}$;
B.2;
C.$-2$;
D.$-2\sqrt {2}$.
答案:
【解析】:
本题主要考察立方根的定义及计算。
根据立方根的定义,我们需要找到一个数$x$,满足$x^3 = -8$。
通过计算,我们可以得出$(-2)^3 = -8$,
所以$-8$的立方根是$-2$。
【答案】:
C. $-2$
本题主要考察立方根的定义及计算。
根据立方根的定义,我们需要找到一个数$x$,满足$x^3 = -8$。
通过计算,我们可以得出$(-2)^3 = -8$,
所以$-8$的立方根是$-2$。
【答案】:
C. $-2$
3. 下列说法正确的是 (
A.$-81的平方根是-9$;
B.$\sqrt {81}的平方根是\pm 9$;
C.$x+\sqrt {x^{2}}= 2x$;
D.$-\sqrt [5]{a^{2}+1}$一定是负数.
D
)A.$-81的平方根是-9$;
B.$\sqrt {81}的平方根是\pm 9$;
C.$x+\sqrt {x^{2}}= 2x$;
D.$-\sqrt [5]{a^{2}+1}$一定是负数.
答案:
【解析】:
本题主要考察平方根、算术平方根、立方根的性质以及代数式的化简。
A选项:根据平方根的定义,一个负数没有实数平方根,因为任何实数的平方都是非负的。所以,$-81$没有实数平方根,故A选项错误。
B选项:首先,$\sqrt{81} = 9$,因为$9 × 9 = 81$。然后,求$9$的平方根,得到$\pm 3$,因为$3 × 3 = 9$且$(-3) × (-3) = 9$。所以,$\sqrt{81}$的平方根是$\pm 3$,不是$\pm 9$,故B选项错误。
C选项:对于$x + \sqrt{x^2}$,当$x \geq 0$时,$\sqrt{x^2} = x$,所以$x + \sqrt{x^2} = 2x$;当$x < 0$时,$\sqrt{x^2} = -x$,所以$x + \sqrt{x^2} = 0$。因此,C选项只在$x \geq 0$时成立,不是对所有$x$都成立,故C选项错误。
D选项:对于$-\sqrt[5]{a^2 + 1}$,由于$a^2 \geq 0$,所以$a^2 + 1 > 0$。因此,$\sqrt[5]{a^2 + 1} > 0$,那么$-\sqrt[5]{a^2 + 1} < 0$。所以,D选项正确。
【答案】:
D
本题主要考察平方根、算术平方根、立方根的性质以及代数式的化简。
A选项:根据平方根的定义,一个负数没有实数平方根,因为任何实数的平方都是非负的。所以,$-81$没有实数平方根,故A选项错误。
B选项:首先,$\sqrt{81} = 9$,因为$9 × 9 = 81$。然后,求$9$的平方根,得到$\pm 3$,因为$3 × 3 = 9$且$(-3) × (-3) = 9$。所以,$\sqrt{81}$的平方根是$\pm 3$,不是$\pm 9$,故B选项错误。
C选项:对于$x + \sqrt{x^2}$,当$x \geq 0$时,$\sqrt{x^2} = x$,所以$x + \sqrt{x^2} = 2x$;当$x < 0$时,$\sqrt{x^2} = -x$,所以$x + \sqrt{x^2} = 0$。因此,C选项只在$x \geq 0$时成立,不是对所有$x$都成立,故C选项错误。
D选项:对于$-\sqrt[5]{a^2 + 1}$,由于$a^2 \geq 0$,所以$a^2 + 1 > 0$。因此,$\sqrt[5]{a^2 + 1} > 0$,那么$-\sqrt[5]{a^2 + 1} < 0$。所以,D选项正确。
【答案】:
D
4. 下列说法正确的是 (
A.无限小数都是无理数;
B.带根号的数都是无理数;
C.无理数都是无限小数;
D.无理数都是带根号的数.
C
)A.无限小数都是无理数;
B.带根号的数都是无理数;
C.无理数都是无限小数;
D.无理数都是带根号的数.
答案:
【解析】:
本题主要考察对无理数和有理数定义的理解,以及无理数和有理数之间的区别。
A选项:无限小数包括无限循环小数和无限不循环小数,其中只有无限不循环小数是无理数,所以A选项错误;
B选项:带根号的数不一定都是无理数,例如$\sqrt{4} = 2$,这是一个有理数,所以B选项错误;
C选项:无理数的定义是无限不循环小数,这自然满足无限小数的定义,所以C选项正确;
D选项:无理数不仅仅包括带根号的数,例如π就是一个无理数,但它并不带根号,所以D选项错误。
【答案】:
C
本题主要考察对无理数和有理数定义的理解,以及无理数和有理数之间的区别。
A选项:无限小数包括无限循环小数和无限不循环小数,其中只有无限不循环小数是无理数,所以A选项错误;
B选项:带根号的数不一定都是无理数,例如$\sqrt{4} = 2$,这是一个有理数,所以B选项错误;
C选项:无理数的定义是无限不循环小数,这自然满足无限小数的定义,所以C选项正确;
D选项:无理数不仅仅包括带根号的数,例如π就是一个无理数,但它并不带根号,所以D选项错误。
【答案】:
C
5. 下列计算正确的是 (
A.$\sqrt {3}+\sqrt {5}= \sqrt {8}$;
B.$5\sqrt {x}-2\sqrt {x}= 3$;
C.$2\sqrt {x}-3\sqrt {x}= 2-3\sqrt {x}$;
D.$2\sqrt {x}+3\sqrt {x}= 5\sqrt {x}$.
D
)A.$\sqrt {3}+\sqrt {5}= \sqrt {8}$;
B.$5\sqrt {x}-2\sqrt {x}= 3$;
C.$2\sqrt {x}-3\sqrt {x}= 2-3\sqrt {x}$;
D.$2\sqrt {x}+3\sqrt {x}= 5\sqrt {x}$.
答案:
【解析】:
本题主要考察二次根式的加减法。
A. 对于 $\sqrt{3} + \sqrt{5}$,由于$\sqrt{3}$与$\sqrt{5}$不是同类二次根式,因此不能合并。所以,$\sqrt{3} + \sqrt{5} \neq \sqrt{8}$,故A选项错误。
B. 对于 $5\sqrt{x} - 2\sqrt{x}$,由于它们是同类二次根式,可以合并。计算得 $5\sqrt{x} - 2\sqrt{x} = 3\sqrt{x}$,与选项给出的 $3$ 不符,故B选项错误。
C. 对于 $2\sqrt{x} - 3\sqrt{x}$,同样由于它们是同类二次根式,可以合并。计算得 $2\sqrt{x} - 3\sqrt{x} = -\sqrt{x}$,与选项给出的 $2-3\sqrt{x}$ 不符,故C选项错误。
D. 对于 $2\sqrt{x} + 3\sqrt{x}$,由于它们是同类二次根式,可以合并。计算得 $2\sqrt{x} + 3\sqrt{x} = 5\sqrt{x}$,与选项给出的 $5\sqrt{x}$ 相符,故D选项正确。
【答案】:
D
本题主要考察二次根式的加减法。
A. 对于 $\sqrt{3} + \sqrt{5}$,由于$\sqrt{3}$与$\sqrt{5}$不是同类二次根式,因此不能合并。所以,$\sqrt{3} + \sqrt{5} \neq \sqrt{8}$,故A选项错误。
B. 对于 $5\sqrt{x} - 2\sqrt{x}$,由于它们是同类二次根式,可以合并。计算得 $5\sqrt{x} - 2\sqrt{x} = 3\sqrt{x}$,与选项给出的 $3$ 不符,故B选项错误。
C. 对于 $2\sqrt{x} - 3\sqrt{x}$,同样由于它们是同类二次根式,可以合并。计算得 $2\sqrt{x} - 3\sqrt{x} = -\sqrt{x}$,与选项给出的 $2-3\sqrt{x}$ 不符,故C选项错误。
D. 对于 $2\sqrt{x} + 3\sqrt{x}$,由于它们是同类二次根式,可以合并。计算得 $2\sqrt{x} + 3\sqrt{x} = 5\sqrt{x}$,与选项给出的 $5\sqrt{x}$ 相符,故D选项正确。
【答案】:
D
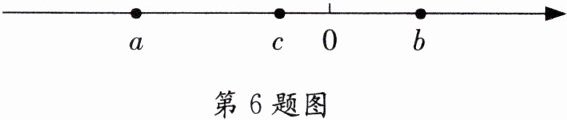
6. 已知三个实数$a$、$b$、$c$在数轴上对应的点如图所示,则$|a-b|+|c-a|-|c+b|$的值可能是 (
A.$2a$;
B.$2b$;
C.$2c$;
D.$-2a$.
D
)
A.$2a$;
B.$2b$;
C.$2c$;
D.$-2a$.
答案:
【解析】:
首先,根据数轴上的点的位置,可以确定$a$、$b$、$c$的大小关系。
从数轴上可以看出,$a \lt c \lt 0 \lt b$,且$\left | b \right | \gt \left | a \right | \gt \left | c \right | $。
接下来,根据这些关系,去掉绝对值符号:
对于$\left | a-b \right | $,因为$a \lt b$,所以$\left | a-b \right | =b-a$;
对于$\left | c-a \right | $,因为$c \gt a$,所以$\left | c-a \right |=c-a$;
对于$\left | c+b \right | $,因为$c \lt 0$,$b \gt 0$,且$\left | b \right | \gt \left | c \right | $,所以$c+b \gt 0$,$\left | c+b \right |=c+b$。
将上述结果代入原式,得到:
$\left | a-b \right | +\left | c-a \right | -\left | c+b \right |=(b-a)+(c-a)-(c+b)=b-a+c-a-c-b=-2a$。
【答案】:
D.$-2a$。
首先,根据数轴上的点的位置,可以确定$a$、$b$、$c$的大小关系。
从数轴上可以看出,$a \lt c \lt 0 \lt b$,且$\left | b \right | \gt \left | a \right | \gt \left | c \right | $。
接下来,根据这些关系,去掉绝对值符号:
对于$\left | a-b \right | $,因为$a \lt b$,所以$\left | a-b \right | =b-a$;
对于$\left | c-a \right | $,因为$c \gt a$,所以$\left | c-a \right |=c-a$;
对于$\left | c+b \right | $,因为$c \lt 0$,$b \gt 0$,且$\left | b \right | \gt \left | c \right | $,所以$c+b \gt 0$,$\left | c+b \right |=c+b$。
将上述结果代入原式,得到:
$\left | a-b \right | +\left | c-a \right | -\left | c+b \right |=(b-a)+(c-a)-(c+b)=b-a+c-a-c-b=-2a$。
【答案】:
D.$-2a$。
7. $\sqrt {(-9)^{2}}$的平方根为
$\pm 3$
.
答案:
【解析】:
首先计算$\sqrt{(-9)^{2}}$,
由于任何数的平方都是非负的,所以$(-9)^{2} = 81$,
再对81开平方,得到$\sqrt{81} = 9$,
接下来,求9的平方根,
一个正数的平方根有两个值,一个正数和一个负数,
所以9的平方根为$\pm 3$。
【答案】:
$\pm 3$
首先计算$\sqrt{(-9)^{2}}$,
由于任何数的平方都是非负的,所以$(-9)^{2} = 81$,
再对81开平方,得到$\sqrt{81} = 9$,
接下来,求9的平方根,
一个正数的平方根有两个值,一个正数和一个负数,
所以9的平方根为$\pm 3$。
【答案】:
$\pm 3$
8. 计算:$-\sqrt [3]{0.125}=$
$-0.5$
.
答案:
【解析】:
本题考查立方根的计算。
首先,我们需要找到一个数,它的立方等于0.125。
我们知道:
$0.5 × 0.5 × 0.5 = 0.125$
所以,$0.5^3 = 0.125$。
因此,$\sqrt[3]{0.125} = 0.5$。
再考虑到题目中的负号,所以:
$-\sqrt[3]{0.125} = -0.5$
【答案】:
$-0.5$
本题考查立方根的计算。
首先,我们需要找到一个数,它的立方等于0.125。
我们知道:
$0.5 × 0.5 × 0.5 = 0.125$
所以,$0.5^3 = 0.125$。
因此,$\sqrt[3]{0.125} = 0.5$。
再考虑到题目中的负号,所以:
$-\sqrt[3]{0.125} = -0.5$
【答案】:
$-0.5$
9. 计算:$\sqrt [3]{(-4)^{3}}=$
-4
.
答案:
【解析】:
本题主要考查立方根的计算。
对于任意实数$a$,有$\sqrt[3]{a^{3}} = a$,这是立方根的基本性质。
应用这一性质到题目中给定的表达式$\sqrt[3]{(-4)^{3}}$,
我们可以直接得出结果。
【答案】:
$\sqrt[3]{(-4)^{3}} = -4$。
本题主要考查立方根的计算。
对于任意实数$a$,有$\sqrt[3]{a^{3}} = a$,这是立方根的基本性质。
应用这一性质到题目中给定的表达式$\sqrt[3]{(-4)^{3}}$,
我们可以直接得出结果。
【答案】:
$\sqrt[3]{(-4)^{3}} = -4$。
10. 在数轴上表示$-\sqrt {3}的点与表示x$的点的距离为
$|x + \sqrt{3}|$
.
答案:
【解析】:
本题主要考查数轴上两点间的距离公式。
在数轴上,两点间的距离等于它们对应数的差的绝对值。
设数轴上表示$-\sqrt{3}$的点为A,表示$x$的点为B,则A、B两点间的距离为:
$AB = |x - (-\sqrt{3})| = |x + \sqrt{3}|$
【答案】:
$|x + \sqrt{3}|$
本题主要考查数轴上两点间的距离公式。
在数轴上,两点间的距离等于它们对应数的差的绝对值。
设数轴上表示$-\sqrt{3}$的点为A,表示$x$的点为B,则A、B两点间的距离为:
$AB = |x - (-\sqrt{3})| = |x + \sqrt{3}|$
【答案】:
$|x + \sqrt{3}|$
11. 比较大小:$2\sqrt {3}$
<
$3\sqrt {2}$.
答案:
【解析】:
首先,为了比较$2\sqrt{3}$和$3\sqrt{2}$的大小,我们可以将它们都平方,然后比较得到的数值。
计算$(2\sqrt{3})^{2}$,得到:
$(2\sqrt{3})^{2} = 4 × 3 = 12$
计算$(3\sqrt{2})^{2}$,得到:
$(3\sqrt{2})^{2} = 9 × 2 = 18$
由于$12 < 18$,
根据平方数的性质,当两个数都是正数时,平方小的原数也小,
所以我们可以得出:
$2\sqrt{3} < 3\sqrt{2}$
【答案】:
$<$
首先,为了比较$2\sqrt{3}$和$3\sqrt{2}$的大小,我们可以将它们都平方,然后比较得到的数值。
计算$(2\sqrt{3})^{2}$,得到:
$(2\sqrt{3})^{2} = 4 × 3 = 12$
计算$(3\sqrt{2})^{2}$,得到:
$(3\sqrt{2})^{2} = 9 × 2 = 18$
由于$12 < 18$,
根据平方数的性质,当两个数都是正数时,平方小的原数也小,
所以我们可以得出:
$2\sqrt{3} < 3\sqrt{2}$
【答案】:
$<$
12. 计算:$3\sqrt {5}-\frac {3}{2}\sqrt {5}= $
$\frac{3}{2}\sqrt{5}$
.
答案:
【解析】:
本题考查二次根式的加减法。
首先,我们需要理解二次根式的加减法原则,即只有同类二次根式才能进行加减运算,且加减时,系数相加减,根号部分保持不变。
题目中的两项 $3\sqrt{5}$ 和 $-\frac{3}{2}\sqrt{5}$ 是同类二次根式,因为它们的根号部分都是 $\sqrt{5}$。
根据二次根式的加减法原则,我们可以将这两项的系数进行相减:
$3\sqrt{5} - \frac{3}{2}\sqrt{5} = \left(3 - \frac{3}{2}\right)\sqrt{5}$
接着,我们计算系数的差:
$3 - \frac{3}{2} = \frac{6}{2} - \frac{3}{2} = \frac{3}{2}$
最后,将计算得到的系数与根号部分相乘,得到最终结果:
$\frac{3}{2}\sqrt{5}$
【答案】:
$\frac{3}{2}\sqrt{5}$
本题考查二次根式的加减法。
首先,我们需要理解二次根式的加减法原则,即只有同类二次根式才能进行加减运算,且加减时,系数相加减,根号部分保持不变。
题目中的两项 $3\sqrt{5}$ 和 $-\frac{3}{2}\sqrt{5}$ 是同类二次根式,因为它们的根号部分都是 $\sqrt{5}$。
根据二次根式的加减法原则,我们可以将这两项的系数进行相减:
$3\sqrt{5} - \frac{3}{2}\sqrt{5} = \left(3 - \frac{3}{2}\right)\sqrt{5}$
接着,我们计算系数的差:
$3 - \frac{3}{2} = \frac{6}{2} - \frac{3}{2} = \frac{3}{2}$
最后,将计算得到的系数与根号部分相乘,得到最终结果:
$\frac{3}{2}\sqrt{5}$
【答案】:
$\frac{3}{2}\sqrt{5}$
13. 计算:$[(\sqrt {2})^{3}-3\sqrt {2}]÷\sqrt {2}=$
$-1$
.
答案:
解:$\begin{aligned}[(\sqrt{2})^{3} - 3\sqrt{2}] ÷ \sqrt{2}&= [(\sqrt{2} × \sqrt{2} × \sqrt{2}) - 3\sqrt{2}] ÷ \sqrt{2}\\&= [(2 × \sqrt{2}) - 3\sqrt{2}] ÷ \sqrt{2}\\&= (2\sqrt{2} - 3\sqrt{2}) ÷ \sqrt{2}\\&= (-\sqrt{2}) ÷ \sqrt{2}\\&= -1\end{aligned}$
故答案为:$-1$
故答案为:$-1$
14. 计算:$\sqrt {5}÷(\sqrt {3})^{2}+(\sqrt {5})^{3}÷(\sqrt {5})^{2}= $
$\frac{4\sqrt{5}}{3}$
.
答案:
【解析】:
本题主要考察二次根式的乘除运算以及幂的运算法则。
首先,我们需要将题目中的表达式进行拆分和化简。
根据幂的运算法则,$(\sqrt{3})^{2} = 3$,$(\sqrt{5})^{3} = 5\sqrt{5}$,$(\sqrt{5})^{2} = 5$。
然后,我们将这些结果代入原式,得到:
$\sqrt{5} ÷ 3 + 5\sqrt{5} ÷ 5$
接着,我们进行二次根式的除法运算,得到:
$\frac{\sqrt{5}}{3} + \sqrt{5}$
最后,我们将两项合并,得到:
$\frac{\sqrt{5}}{3} + \frac{3\sqrt{5}}{3} = \frac{4\sqrt{5}}{3}$
【答案】:
$\frac{4\sqrt{5}}{3}$
本题主要考察二次根式的乘除运算以及幂的运算法则。
首先,我们需要将题目中的表达式进行拆分和化简。
根据幂的运算法则,$(\sqrt{3})^{2} = 3$,$(\sqrt{5})^{3} = 5\sqrt{5}$,$(\sqrt{5})^{2} = 5$。
然后,我们将这些结果代入原式,得到:
$\sqrt{5} ÷ 3 + 5\sqrt{5} ÷ 5$
接着,我们进行二次根式的除法运算,得到:
$\frac{\sqrt{5}}{3} + \sqrt{5}$
最后,我们将两项合并,得到:
$\frac{\sqrt{5}}{3} + \frac{3\sqrt{5}}{3} = \frac{4\sqrt{5}}{3}$
【答案】:
$\frac{4\sqrt{5}}{3}$
15. 绝对值小于$\sqrt {15}$的所有整数是
$-3$,$-2$,$-1$,$0$,$1$,$2$,$3$
.
答案:
解:因为$9 < 15 < 16$,所以$\sqrt{9} < \sqrt{15} < \sqrt{16}$,即$3 < \sqrt{15} < 4$。
绝对值小于$\sqrt{15}$的整数,即满足$|x| < \sqrt{15}$的整数$x$,所以$-\sqrt{15} < x < \sqrt{15}$。
又因为$\sqrt{15}$在$3$和$4$之间,所以$x$的取值为$-3$,$-2$,$-1$,$0$,$1$,$2$,$3$。
答案:$-3$,$-2$,$-1$,$0$,$1$,$2$,$3$
绝对值小于$\sqrt{15}$的整数,即满足$|x| < \sqrt{15}$的整数$x$,所以$-\sqrt{15} < x < \sqrt{15}$。
又因为$\sqrt{15}$在$3$和$4$之间,所以$x$的取值为$-3$,$-2$,$-1$,$0$,$1$,$2$,$3$。
答案:$-3$,$-2$,$-1$,$0$,$1$,$2$,$3$
16. 若长方形的长为$\sqrt {6}cm$,面积为$8\sqrt {3}cm^{2}$,则长方形的宽约为
5.66
$cm$($\sqrt {2}\approx 1.414$,$\sqrt {3}\approx 1.732$,结果保留 2 位小数).
答案:
解:长方形的宽 = 面积 ÷ 长,即宽 = $8\sqrt{3} ÷ \sqrt{6}$。
化简:$8\sqrt{3} ÷ \sqrt{6} = 8\sqrt{\frac{3}{6}} = 8\sqrt{\frac{1}{2}} = 8×\frac{\sqrt{2}}{2} = 4\sqrt{2}$。
将$\sqrt{2} \approx 1.414$代入,得宽 ≈ $4×1.414 = 5.656$,保留两位小数为$5.66$。
5.66
化简:$8\sqrt{3} ÷ \sqrt{6} = 8\sqrt{\frac{3}{6}} = 8\sqrt{\frac{1}{2}} = 8×\frac{\sqrt{2}}{2} = 4\sqrt{2}$。
将$\sqrt{2} \approx 1.414$代入,得宽 ≈ $4×1.414 = 5.656$,保留两位小数为$5.66$。
5.66
查看更多完整答案,请扫码查看


