15. 求下列各式的值:
(1)$|\sqrt{2}-2|$; (2)$-|2-\sqrt{3}|$;
(3)$|\sqrt{3}-\sqrt{5}|$; (4)$|\frac{\pi}{4}-\frac{\pi}{3}|$.
(1)$|\sqrt{2}-2|$; (2)$-|2-\sqrt{3}|$;
(3)$|\sqrt{3}-\sqrt{5}|$; (4)$|\frac{\pi}{4}-\frac{\pi}{3}|$.
答案:
(1)解:因为$\sqrt{2}\approx1.414\lt2$,所以$\sqrt{2}-2\lt0$,则$|\sqrt{2}-2|=2-\sqrt{2}$。
(2)解:因为$\sqrt{3}\approx1.732\lt2$,所以$2-\sqrt{3}\gt0$,则$-|2-\sqrt{3}|=-(2-\sqrt{3})=\sqrt{3}-2$。
(3)解:因为$\sqrt{3}\approx1.732$,$\sqrt{5}\approx2.236$,$\sqrt{3}\lt\sqrt{5}$,所以$\sqrt{3}-\sqrt{5}\lt0$,则$|\sqrt{3}-\sqrt{5}|=\sqrt{5}-\sqrt{3}$。
(4)解:$\frac{\pi}{4}-\frac{\pi}{3}=\frac{3\pi - 4\pi}{12}=-\frac{\pi}{12}\lt0$,则$|\frac{\pi}{4}-\frac{\pi}{3}|=\frac{\pi}{12}$。
(1)解:因为$\sqrt{2}\approx1.414\lt2$,所以$\sqrt{2}-2\lt0$,则$|\sqrt{2}-2|=2-\sqrt{2}$。
(2)解:因为$\sqrt{3}\approx1.732\lt2$,所以$2-\sqrt{3}\gt0$,则$-|2-\sqrt{3}|=-(2-\sqrt{3})=\sqrt{3}-2$。
(3)解:因为$\sqrt{3}\approx1.732$,$\sqrt{5}\approx2.236$,$\sqrt{3}\lt\sqrt{5}$,所以$\sqrt{3}-\sqrt{5}\lt0$,则$|\sqrt{3}-\sqrt{5}|=\sqrt{5}-\sqrt{3}$。
(4)解:$\frac{\pi}{4}-\frac{\pi}{3}=\frac{3\pi - 4\pi}{12}=-\frac{\pi}{12}\lt0$,则$|\frac{\pi}{4}-\frac{\pi}{3}|=\frac{\pi}{12}$。
16. 已知$a$、$b$互为相反数,$c$、$d$互为倒数,求$\frac{a^{2}-b^{2}}{a^{2}+b^{2}}-\sqrt{cd}$的值.
答案:
【解析】:
本题主要考察相反数和倒数的性质以及代数表达式的化简。
首先,由于$a$和$b$互为相反数,根据相反数的定义,有$a = -b$,从而可以得到$a + b = 0$。
其次,$c$和$d$互为倒数,根据倒数的定义,有$cd = 1$。
接下来,将原式进行化简。
原式可以拆分为两部分:$\frac{a^{2} - b^{2}}{a^{2} + b^{2}}$ 和 $\sqrt{cd}$。
对于第一部分,利用平方差公式,有$a^{2} - b^{2} = (a + b)(a - b)$。
由于$a + b = 0$,所以$a^{2} - b^{2} = 0$。
又因为$a^{2} + b^{2} \neq 0$(除非$a=b=0$,但在这个问题中,$a$和$b$作为分母的组成部分,不能同时为0),
所以$\frac{a^{2} - b^{2}}{a^{2} + b^{2}} = 0$。
对于第二部分,由于$cd = 1$,所以$\sqrt{cd} = \sqrt{1} = 1$。
最后,将两部分的结果代入原式,得到:
$\frac{a^{2} - b^{2}}{a^{2} + b^{2}} - \sqrt{cd} = 0 - 1 = -1$。
【答案】:
$-1$。
本题主要考察相反数和倒数的性质以及代数表达式的化简。
首先,由于$a$和$b$互为相反数,根据相反数的定义,有$a = -b$,从而可以得到$a + b = 0$。
其次,$c$和$d$互为倒数,根据倒数的定义,有$cd = 1$。
接下来,将原式进行化简。
原式可以拆分为两部分:$\frac{a^{2} - b^{2}}{a^{2} + b^{2}}$ 和 $\sqrt{cd}$。
对于第一部分,利用平方差公式,有$a^{2} - b^{2} = (a + b)(a - b)$。
由于$a + b = 0$,所以$a^{2} - b^{2} = 0$。
又因为$a^{2} + b^{2} \neq 0$(除非$a=b=0$,但在这个问题中,$a$和$b$作为分母的组成部分,不能同时为0),
所以$\frac{a^{2} - b^{2}}{a^{2} + b^{2}} = 0$。
对于第二部分,由于$cd = 1$,所以$\sqrt{cd} = \sqrt{1} = 1$。
最后,将两部分的结果代入原式,得到:
$\frac{a^{2} - b^{2}}{a^{2} + b^{2}} - \sqrt{cd} = 0 - 1 = -1$。
【答案】:
$-1$。
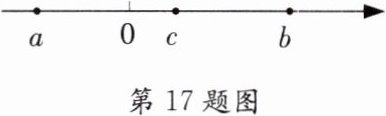
17. 已知$a$、$b$、$c$三个数在数轴上对应的点如图所示,求$|a-b|+|c-a|-|c+b|-|a-c|$的值.

答案:
解:由数轴可知:$a < 0 < c < b$,且$|a| < |b|$,
$\therefore a - b < 0$,$c - a > 0$,$c + b > 0$,$a - c < 0$,
$\therefore |a - b| = b - a$,$|c - a| = c - a$,$|c + b| = c + b$,$|a - c| = c - a$,
$\therefore |a - b| + |c - a| - |c + b| - |a - c|$
$= (b - a) + (c - a) - (c + b) - (c - a)$
$= b - a + c - a - c - b - c + a$
$= -a - c$.
$\therefore a - b < 0$,$c - a > 0$,$c + b > 0$,$a - c < 0$,
$\therefore |a - b| = b - a$,$|c - a| = c - a$,$|c + b| = c + b$,$|a - c| = c - a$,
$\therefore |a - b| + |c - a| - |c + b| - |a - c|$
$= (b - a) + (c - a) - (c + b) - (c - a)$
$= b - a + c - a - c - b - c + a$
$= -a - c$.
思维与拓展4
代数式$|x-1|+|x-2|+|x-3|$是否有最小值? 如果有,请把它求出来;如果没有,请说明理由.
代数式$|x-1|+|x-2|+|x-3|$是否有最小值? 如果有,请把它求出来;如果没有,请说明理由.
答案:
【解析】:
本题主要考查绝对值的性质和实数的绝对值大小比较。
要求代数式$|x-1|+|x-2|+|x-3|$的最小值,可以考虑该代数式表示的是数轴上某一点到点$1$,$2$,$3$的距离之和。
为了找到使这个距离和最小的$x$,可以考虑数轴上的几何意义。
当$x$在$1$和$3$之间(包括$1$和$3$)时,$|x-1|+|x-3|$表示的是$x$到$1$和$3$的距离和,这个距离和是固定的,为$2$。
同时,$|x-2|$表示的是$x$到$2$的距离,当$x=2$时,$|x-2|=0$,此时整个代数式的值最小。
因此,当$x=2$时,代数式$|x-1|+|x-2|+|x-3|$取得最小值。
【答案】:
当$x=2$时,代数式$|x-1|+|x-2|+|x-3|$的最小值为$2$。
本题主要考查绝对值的性质和实数的绝对值大小比较。
要求代数式$|x-1|+|x-2|+|x-3|$的最小值,可以考虑该代数式表示的是数轴上某一点到点$1$,$2$,$3$的距离之和。
为了找到使这个距离和最小的$x$,可以考虑数轴上的几何意义。
当$x$在$1$和$3$之间(包括$1$和$3$)时,$|x-1|+|x-3|$表示的是$x$到$1$和$3$的距离和,这个距离和是固定的,为$2$。
同时,$|x-2|$表示的是$x$到$2$的距离,当$x=2$时,$|x-2|=0$,此时整个代数式的值最小。
因此,当$x=2$时,代数式$|x-1|+|x-2|+|x-3|$取得最小值。
【答案】:
当$x=2$时,代数式$|x-1|+|x-2|+|x-3|$的最小值为$2$。
查看更多完整答案,请扫码查看


