《2025年中学生世界八年级数学上册沪教版五四制》

14. 把下列各式化成最简二次根式:
(1)$\sqrt {18x^{3}y^{4}};$ (2)$\sqrt {25m^{4}+225m^{2}}(m＞0);$
(3)$\sqrt {3x^{2}-6x+3}(x＞1);$ (4)$\sqrt {\frac {-x^{3}}{(x-1)^{2}}}.$

答案：
(1)解：$\sqrt{18x^{3}y^{4}}=\sqrt{9x^{2}y^{4}\cdot2x}=3xy^{2}\sqrt{2x}$
(2)解：$\sqrt{25m^{4}+225m^{2}}=\sqrt{25m^{2}(m^{2}+9)}=5m\sqrt{m^{2}+9}$
(3)解：$\sqrt{3x^{2}-6x+3}=\sqrt{3(x^{2}-2x+1)}=\sqrt{3(x-1)^{2}}=(x-1)\sqrt{3}$
(4)解：由$\frac{-x^{3}}{(x-1)^{2}}\geq0$且$(x-1)^{2}＞0$，得$-x^{3}\geq0$，即$x^{3}\leq0$，所以$x\leq0$。又因为$x-1\neq0$，所以$x\neq1$，综上$x\leq0$。
$\sqrt{\frac{-x^{3}}{(x-1)^{2}}}=\frac{\sqrt{-x^{3}}}{\vert x-1\vert}$，因为$x\leq0$，所以$x-1＜0$，$\vert x-1\vert=1 - x$；$\sqrt{-x^{3}}=\sqrt{-x\cdot x^{2}}=\vert x\vert\sqrt{-x}=-x\sqrt{-x}$。
所以原式$=\frac{-x\sqrt{-x}}{1 - x}=\frac{-x\sqrt{-x}}{1 - x}$

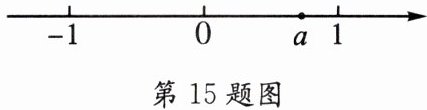
15. 已知实数a在数轴上的位置如图所示,化简:$|1-a|+\sqrt {a^{2}}.$

答案： 【解析】：
本题可根据数轴得出$a$的取值范围，再根据绝对值和二次根式的性质对原式进行化简。
步骤一：根据数轴确定$a$的取值范围
由数轴可知$0\lt a\lt1$。
步骤二：判断$1 - a$的正负性
因为$0\lt a\lt1$，不等式两边同时乘以$-1$，不等号方向改变，可得$-1\lt -a\lt0$，再在不等式两边同时加$1$，可得$1 - 1\lt 1 - a\lt 1 + 0$，即$0\lt 1 - a\lt 1$，所以$1 - a\gt 0$。
步骤三：根据绝对值和二次根式的性质化简原式
化简$\vert1 - a\vert$：
根据绝对值的性质：当$x\gt 0$时，$\vert x\vert = x$。
因为$1 - a\gt 0$，所以$\vert1 - a\vert = 1 - a$。
化简$\sqrt{a^2}$：
根据二次根式的性质：$\sqrt{x^2}=\vert x\vert$，可得$\sqrt{a^2}=\vert a\vert$。
再根据绝对值的性质：当$x\gt 0$时，$\vert x\vert = x$。
因为$0\lt a\lt1$，即$a\gt 0$，所以$\vert a\vert = a$，即$\sqrt{a^2}=a$。
步骤四：计算化简后的式子
将$\vert1 - a\vert = 1 - a$，$\sqrt{a^2}=a$代入$\vert1 - a\vert + \sqrt{a^2}$可得：
$\vert1 - a\vert + \sqrt{a^2}=1 - a + a = 1$。
【答案】：
$1$

思维与拓展9
已知实数m满足$\sqrt {(2024-m)^{2}}+\sqrt {m-2025}= m$,求$m-2024^{2}$的值.

答案： 【解析】：
本题主要考查二次根式的性质及其化简。
首先，由于方程中存在$\sqrt {m-2025}$，根据二次根式的定义，被开方数必须大于等于0，所以有：
$m - 2025 \geq 0$，
解得：
$m \geq 2025$，
当$m \geq 2025$时，$2024 - m ＜ 0$，
所以，$\sqrt {(2024-m)^{2}}$可以化简为$m - 2024$（因为当$a ＜ 0$时，$\sqrt {a^{2}} = -a$）。
将化简后的结果代入原方程，得到：
$m - 2024 + \sqrt {m - 2025} = m$，
移项，得到：
$\sqrt {m - 2025} = 2024$，
两边平方，得到：
$m - 2025 = 2024^{2}$，
最后，解出$m - 2024^{2}$的值：
$m - 2024^{2} = 2025$。
【答案】：
$m - 2024^{2} = 2025$。