《2025年实验班提优训练九年级科学上册浙教版》

8. 如图所示,根据杠杆的平衡条件测量某种液体的密度,所用器材:轻质杠杆(自身重力忽略不计)、容积为 100 mL 的空桶、重为 0.5 N 的物体 M、刻度尺、细线。

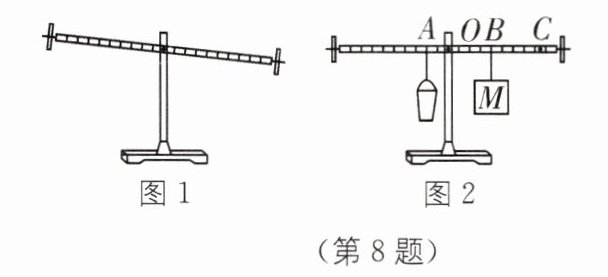
(1)如图 1 所示,为了使杠杆在水平位置平衡,应将杠杆右端的平衡螺母向左调节;调节杠杆在水平位置平衡的目的是消除杠杆自重对实验结果的影响,并且方便测量力臂的长度。
(2)把空桶悬挂在 A 点,物体 M 悬挂在 B 点时,杠杆再次在水平位置平衡,测得 OA 的长度为 10 cm,OB 的长度为 20 cm,则空桶重为1N。
(3)若此时往 A 点的空桶内注满某种液体,调节物体 M 到 C 点时,杠杆在水平位置重新平衡,测得 OC 的长度为 42 cm,则桶内液体的密度为$1.1×10^{3}$$ kg/m^3。$(g 取 10 N/kg)

答案：
(1)左 消除杠杆自重对实验结果的影响,并且方便测量力臂的长度
(2)1
(3)$1.1×10^{3}\ \text{kg/m}^{3}$ [解析]
(1)根据天平调平衡的方法可知,此时应该将平衡螺母向左调节;调节杠杆在水平位置平衡的目的是消除杠杆自重对实验结果的影响,并且方便在接下来的实验中测量力臂的长度。
(2)设空桶质量为m,$G_{\text{桶}}=mg$,根据杠杆平衡条件$G_{\text{桶}}×10\ \text{cm}=0.5\ \text{N}×20\ \text{cm}$,可求出$G_{\text{桶}}=1\ \text{N}$。
(3)根据题意可知,往A点的空桶内注满某种液体,调节物体M到C点时,杠杆在水平位置重新平衡,$l_{\text{桶}}=10\ \text{cm}=0.1\ \text{m}$,测得OC的长度为$l_{M}=42\ \text{cm}=0.42\ \text{m}$,$G_{\text{桶}}=1\ \text{N}$,设此时液体质量为$m_{\text{液}}$,再次根据杠杆平衡条件可得$(m_{\text{液}}g+G_{\text{桶}})l_{\text{桶}}=G_{M}l_{M}$,由上式并代入数据可得$m_{\text{液}}=0.11\ \text{kg}=110\ \text{g}$,由已知条件可知$V_{\text{液}}=100\ \text{cm}^{3}$,则桶内液体密度$\rho=\frac{m_{\text{液}}}{V_{\text{液}}}=\frac{110\ \text{g}}{100\ \text{cm}^{3}}=1.1\ \text{g/cm}^{3}=1.1×10^{3}\ \text{kg/m}^{3}$。

9. 中考新考法 制作杆秤液体密度计 转换法 (2024·泸州中考)在某届泸州市青少年科技创新大赛中,小明制作的"杆秤液体密度计"如图 1 所示,选取了一根质量不计的硬质轻杆,P 为提挂点,P 点的左侧端点 A 处悬挂透明塑料杯,右侧悬挂秤砣,不计细线质量。将相同体积不同密度的待测液体加入杯中,根据杠杆平衡条件可知,杠杆平衡时,秤砣悬挂点到 P 点的距离与待测液体的密度成一次函数关系,即可在杠杆上均匀标出刻度线来测量液体密度。其制作与测量过程中进行了如下操作。(g 取 10 N/kg)

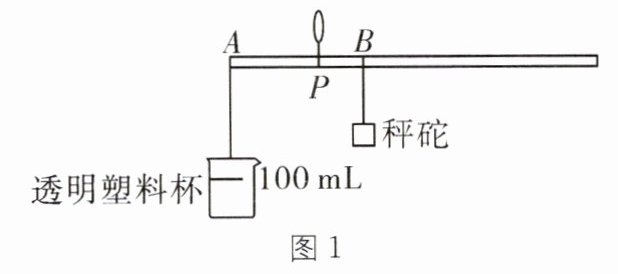
(1)距离左端点 A 处 10 cm 的位置制作提挂点 P;用天平称得空塑料杯质量如图 2 所示,则空塑料杯质量为25g;右侧秤砣采用 50 g 钩码拴上细线制成。

(2)将空塑料杯悬挂在 A 点,调节右侧秤砣细线位置,使杠杆在水平位置平衡,此时细线位置处标记为$"0 g/cm^3",$此刻度线到提挂点 P 距离为5cm。
(3)将 100 mL 密度为$ 1 g/cm^3$的水倒入塑料杯中,在液面处作标记,调节秤砣细线位置使杠杆再次在水平位置平衡,并在此时秤砣细线位置处标记为"1",此刻度线到提挂点 P 的距离为25cm;将"0"到"1"刻度线之间均分 10 等份,则该密度计的分度值为0.1$ g/cm^3;$按该分度值在杠杆上均匀画出刻度线,即杆秤密度计制作完成。
(4)用制作好的密度计测量某一液体密度时,将 100 mL 的液体倒入空塑料杯中,秤砣细线位置如图 3 所示,待测液体密度为0.8$ g/cm^3。$
(5)制作好的密度计不仅能够测出液体的密度,还可以测算某些固体的密度。某次测量时,小明将石块放入空塑料杯中,杠杆平衡时,秤砣细线在"0.5"刻度处,再向杯中加水至 100 mL 标记处(石块浸没),杠杆再次平衡时,秤砣细线在"1.3"刻度处,则小石块的密度为2.5$ g/cm^3。$

答案：
(1)25
(2)5
(3)25 0.1
(4)0.8
(5)2.5 [解析]
(1)物体质量等于砝码质量加上游码对应刻度,即空烧杯质量为$m_{\text{空}}=20\ \text{g}+5\ \text{g}=25\ \text{g}$。
(2)把APB看作杠杆,P为支点,A点受力为$F_{A}=G_{\text{杯}}=m_{\text{杯}}g=0.025\ \text{kg}×10\ \text{N/kg}=0.25\ \text{N}$,B点受力为$F_{B}=G_{\text{钩码}}=m_{\text{钩码}}g=0.05\ \text{kg}×10\ \text{N/kg}=0.5\ \text{N}$,根据杠杆平衡条件,有$F_{A}\cdot AP=F_{B}\cdot PB$,此刻度线到提挂点P距离为$PB=\frac{F_{A}}{F_{B}}× AP=\frac{0.25\ \text{N}}{0.5\ \text{N}}×0.1\ \text{m}=0.05\ \text{m}=5\ \text{cm}$。
(3)100mL密度为$1\ \text{g/cm}^{3}$的水倒入塑料杯中,水的质量为$m_{\text{水}}=\rho_{\text{水}}V_{\text{水}}=1\ \text{g/cm}^{3}×100\ \text{cm}^{3}=100\ \text{g}$,A点受力为$F_{A}'=G_{\text{杯}}+G_{\text{水}}=0.25\ \text{N}+0.1\ \text{kg}×10\ \text{N/kg}=1.25\ \text{N}$,根据杠杆平衡条件,有$F_{A}'\cdot AP=F_{B}\cdot PB'$,此刻度线到提挂点P距离为$PB'=\frac{F_{A}'}{F_{B}}× AP=\frac{1.25\ \text{N}}{0.5\ \text{N}}×0.1\ \text{m}=0.25\ \text{m}=25\ \text{cm}$,"0"到"1"之间共20cm,将"0"到"1"刻度线之间均分10等份,每份2cm,则该密度计的分度值为$0.1\ \text{g/cm}^{3}$。
(4)由图3可知,则待测液体密度为$0.8\ \text{g/cm}^{3}$。
(5)秤砣细线在"0.5"刻度处,此刻度线到"0"距离为10cm,"0.5"刻度线到提挂点P距离为15cm,将石块放入空塑料杯中,杠杆平衡时,秤砣细线在"0.5"刻度处,可得$F_{A1}=\frac{15\ \text{cm}}{10\ \text{cm}}×0.5\ \text{N}=0.75\ \text{N}$,则石块重力为$G_{\text{石}}=F_{A1}-G_{\text{杯}}=0.75\ \text{N}-0.25\ \text{N}=0.5\ \text{N}$,则石块质量为$m_{\text{石}}=\frac{G_{\text{石}}}{g}=\frac{0.5\ \text{N}}{10\ \text{N/kg}}=0.05\ \text{kg}=50\ \text{g}$,秤砣细线在"1.3"刻度处,此刻度线到提挂点P距离为31cm,向杯中加水至100mL标记处(石块浸没),杠杆再次平衡时,秤砣细线在"1.3"刻度处,可得$F_{A2}=\frac{31\ \text{cm}}{10\ \text{cm}}×0.5\ \text{N}=1.55\ \text{N}$,则加入水的重力为$G_{\text{水}}=F_{A2}-F_{A1}=1.55\ \text{N}-0.75\ \text{N}=0.8\ \text{N}$,则加入水的体积为$V_{\text{水}}=\frac{G_{\text{水}}}{\rho_{\text{水}}g}=\frac{0.8\ \text{N}}{1×10^{3}\ \text{kg/m}^{3}×10\ \text{N/kg}}=0.8×10^{-4}\ \text{m}^{3}=80\ \text{cm}^{3}$,则石块体积为$V_{\text{石}}=100\ \text{cm}^{3}-80\ \text{cm}^{3}=20\ \text{cm}^{3}$,所以石块密度为$\rho=\frac{m_{\text{石}}}{V_{\text{石}}}=\frac{50\ \text{g}}{20\ \text{cm}^{3}}=2.5\ \text{g/cm}^{3}$。