《2025年实验班提优训练九年级科学上册浙教版》

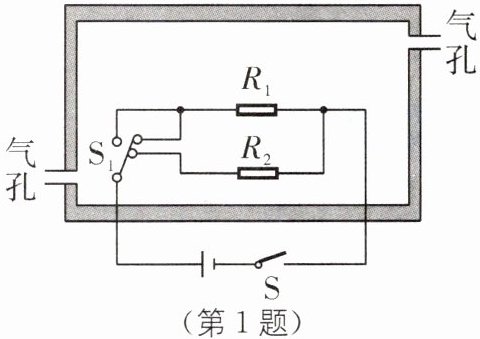
1. 恒温箱广泛应用于医疗、科研、化工等行业部门,如图所示为某恒温箱的工作原理图。S为电源开关,通过控制温控开关$S_{1}$可实现“保温”、“加热”两个挡位间的切换。电源电压$U= 220\ \text{V}$,$R_{1}$、$R_{2}$是电热丝,$R_{1}= 440\ \Omega$,“加热”时恒温箱的电功率$P_{加热}= 550\ \text{W}$。将恒温箱两气孔封闭,闭合开关S,$S_{1}$置于“加热”挡位,箱内温度从$20\ ^{\circ}\text{C}$升至设定的恒温温度,用时130 s,该段时间内的加热效率$\eta =80\%$。恒温箱的容积$V= 2\ \text{m}^{3}$,箱内空气密度$\rho =1.3\ \text{kg/m}^{3}$,箱内空气的比热容$c= 1.0× 10^{3}\ \text{J/(kg}\cdot^{\circ}\text{C)}$。求：
(1)“保温”时恒温箱的电功率；
(2)电热丝$R_{2}$的阻值；
(3)恒温箱的恒温温度。

答案： 1.
(1)110 W
(2)110 Ω
(3)42 ℃
[解析]
(1)由题图可知,当闭合开关S,温控开关S₁置于右边两个触点时,R₁、R₂并联,根据并联电路的电阻特点可知,此时电路中的总电阻最小,由$P=\frac{U^{2}}{R}$可知,电路中的总功率最大,恒温箱处于加热挡;当闭合开关S,温控开关S₁置于左边触点时,电路为R₁的简单电路,电路中的总电阻最大,总功率最小,恒温箱处于保温挡;保温时恒温箱的电功率为$P_{保温}=\frac{U^{2}}{R_{1}}=\frac{(220\ \text{V})^{2}}{440\ \Omega}=110\ \text{W}$。
(2)由于并联电路中各用电器的电功率之和等于电路的总功率,则加热挡工作时R₂的电功率为$P_{2}=P_{加热}-P_{保温}=550\ \text{W}-110\ \text{W}=440\ \text{W}$,则R₂的阻值为$R_{2}=\frac{U^{2}}{P_{2}}=\frac{(220\ \text{V})^{2}}{440\ \text{W}}=110\ \Omega$。
(3)由$P=\frac{W}{t}$可知,恒温箱消耗的电能$W=P_{加热}t'=550\ \text{W}×130\ \text{s}=71\ 500\ \text{J}$,由$\eta=\frac{Q_{吸}}{W}×100\%$可知,恒温箱内气体吸收的热量$Q_{吸}=\eta W=80\%×71\ 500\ \text{J}=57\ 200\ \text{J}$,由$\rho=\frac{m}{V}$可知,恒温箱内气体的质量$m=\rho V=1.3\ \text{kg/m}^{3}×2\ \text{m}^{3}=2.6\ \text{kg}$,由$Q_{吸}=cm(t-t_{0})$可知,恒温箱的恒温温度$t=\frac{Q_{吸}}{cm}+t_{0}=\frac{57\ 200\ \text{J}}{1.0×10^{3}\ \text{J/(kg}\cdot^{\circ}\text{C)}×2.6\ \text{kg}}+20\ ^{\circ}\text{C}=42\ ^{\circ}\text{C}$。

变式1.1 如图1所示为小明家的电饭锅,铭牌上附有中国能效标识,从铭牌上可知该电饭锅能效等级为三级,额定电压为220 V,加热功率为1210 W。电饭锅的简化电路图如图2所示,有加热和保温两挡,由开关S调节,其中$R_{1}和R_{2}$均为发热电阻,且阻值不随着温度的变化而改变。
(变式1.1)
(1)小明想利用如图3所示的电能表测量电饭锅的保温功率,他关闭家里的其他用电器,让电饭锅处于“保温”状态下正常工作,观察到电能表转盘在5 min内转了22圈。则该电饭锅的保温功率为多少？
(2)电阻$R_{1}$、$R_{2}$的阻值分别为多少？
(3)小明上网查询了解到国家标准中规定电饭锅在该加热功率下正常工作时,三级能效的热效率值(电热转化效率)范围为$81\%\leqslant \eta ＜86\%$。他用学过的知识对电饭锅进行测试：在加热状态下,将温度为$23\ ^{\circ}\text{C}$、质量为2.2 kg的水加热到$100\ ^{\circ}\text{C}$,电饭锅正常工作用时700 s。已知$c_{水}= 4.2× 10^{3}\ \text{J/(kg}\cdot^{\circ}\text{C)}$,请你通过计算帮助小明判断该电饭锅的热效率值是否达到三级能效。

答案： 变式1.1
(1)88 W
(2)40 Ω 510 Ω
(3)达到三级能效
[解析]
(1)"3 000 r/(kW·h)"表示每消耗1 kW·h电能,电能表转盘转3 000圈,只让电饭煲在"保温"状态下工作,转盘在5 min内转了22转,消耗的电能为$W=\frac{22\ \text{r}}{3\ 000\ \text{r/(kW·h)}}=\frac{11}{1\ 500}\ \text{kW·h}$,则该电饭锅处于"保温"状态时的功率为$P_{保温}=\frac{W}{t}=\frac{\frac{11}{1\ 500}\ \text{kW·h}}{\frac{5}{60}\ \text{h}}=0.088\ \text{kW}=88\ \text{W}$。
(2)由电路图知,S断开时两电阻串联,电路中电阻较大,功率较小,为保温状态;当S闭合时,电路为R₁的简单电路,电路中电阻较小,功率较大,为加热状态。由$P=\frac{U^{2}}{R}$可得,R₁的电阻$R_{1}=\frac{U^{2}}{P_{加热}}=\frac{(220\ \text{V})^{2}}{1\ 210\ \text{W}}=40\ \Omega$,由$P=\frac{U^{2}}{R}$可得,R₁、R₂的总电阻$R_{总}=\frac{U^{2}}{P_{保温}}=\frac{(220\ \text{V})^{2}}{88\ \text{W}}=550\ \Omega$,R₂的电阻为$R_{2}=R_{总}-R_{1}=550\ \Omega-40\ \Omega=510\ \Omega$。
(3)水吸收的热量$Q_{吸}=c_{水}m\Delta t=4.2×10^{3}\ \text{J/(kg}\cdot^{\circ}\text{C)}×2.2\ \text{kg}×(100\ ^{\circ}\text{C}-23\ ^{\circ}\text{C})=7.114\ 8×10^{5}\ \text{J}$,用时700 s消耗的电能$W'=P_{加热}t'=1\ 210\ \text{W}×700\ \text{s}=8.47×10^{5}\ \text{J}$,该电饭锅的热效率$\eta=\frac{Q_{吸}}{W'}×100\%=\frac{7.114\ 8×10^{5}\ \text{J}}{8.47×10^{5}\ \text{J}}×100\%=84\%$,故该电饭锅的热效率值达到三级能效。