《2025年实验班提优训练九年级科学上册浙教版》

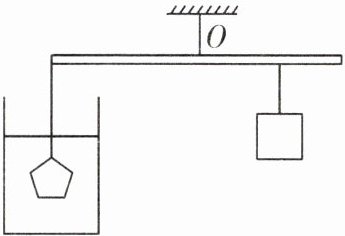
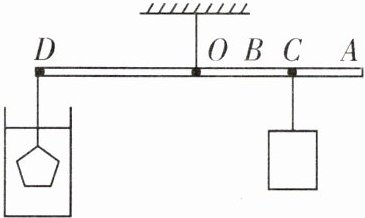
【例3】(余姚重点高中自主招生)如图所示,轻质杆可绕O点转动,分别将质量相同的纯金块、纯银块和金银合金制作的王冠分别悬挂于杆的最左端并浸没水中,将质量与王冠相同的重物对应悬挂在杆上的A、B、C处(图中未画出),杆恰好在水平位置平衡。测得A、C两点间的距离为7cm,B、C两点间的距离为3cm。则王冠中金和银的质量比为( A )。


A.3:7
B.7:3
C.2:5
D.5:2
分析：设纯金块、纯银块、金银合金制作的王冠以及重物的质量为m,纯金块、纯银块、金银合金制作的王冠的密度分别为$ρ_{1}$、$ρ_{2}$、$ρ_{3}$,体积分别为$V_{1}$、$V_{2}$、$V_{3}$,由于$ρ_{1}＞ρ_{3}＞ρ_{2}根据V= \frac{m}{ρ}$可知,三者的体积关系为$V_{1}＜V_{3}＜V_{2}$,浸没在水中时,三者排开水的体积与各自体积相等,根据$F_{浮}= ρ_{水}gV_{排}$可知,三者的浮力关系为$F_{浮1}＜F_{浮3}＜F_{浮2}$当质量相同(重力相同)的纯金块、纯银块和金银合金制作的王冠悬挂于杆的最左端并分别浸没水中时,杆的最左端受到的拉力$F_{拉}= G-F_{浮}$,由于$F_{浮1}＜F_{浮3}＜F_{浮2}$,则$F_{拉1}＞F_{拉3}＞F_{拉2}$,且左边拉力的力臂相同,根据杠杆平衡条件可知,相同的重物对应地悬挂在杆上的A、B、C处,如图所示。

根据阿基米德原理和杠杆平衡条件得,当纯金块悬挂于杆的最左端并浸没水中时有$(mg-ρ_{水}gV_{1})L_{OD}= mg(L_{OB}+L_{BC}+L_{AC})...①$,当纯银块悬挂于杆的最左端并浸没水中时有$(mg-ρ_{水}gV_{2})L_{OD}= mgL_{OB}...②$,当金银合金制作的王冠悬挂于杆的最左端并浸没水中时有$(mg-ρ_{水}gV_{3})L_{OD}= mg(L_{OB}+L_{BC})...③$,用①-②得$(ρ_{水}gV_{2}-ρ_{水}gV_{1})L_{OD}= mg(L_{BC}+L_{AC})...④$,用③-②得$(ρ_{水}gV_{2}-ρ_{水}gV_{3})L_{OD}= mgL_{BC}...⑤$,用$\frac{④}{⑤}得\frac{V_{2}-V_{1}}{V_{2}-V_{3}}= \frac{L_{BC}+L_{AC}}{L_{BC}}= \frac{3cm+7cm}{3cm}= \frac{10}{3}$,化简整理得$V_{3}= \frac{3}{10}V_{1}+\frac{7}{10}V_{2}...⑥$,设王冠中金和银的质量分别为$m_{1}$、$m_{2}$,则王冠的体积$V_{3}= \frac{m_{1}}{ρ_{1}}+\frac{m_{2}}{ρ_{2}}...⑦$,纯金块的密度$ρ_{1}= \frac{m}{V_{1}}...⑧$,纯银块的密度$ρ_{2}= \frac{m}{V_{2}}...⑨$,将⑧⑨代入⑦整理得$V_{3}= \frac{m_{1}}{m}V_{1}+\frac{m_{2}}{m}V_{2}...⑩$,用⑩-⑥得$(\frac{m_{1}}{m}-\frac{3}{10})V_{1}+(\frac{m_{2}}{m}-\frac{7}{10})V_{2}= 0...⑪$,因为$m_{1}+m_{2}= m$,所以$m_{2}= m-m_{1}$,将此式代入⑪,整理得$(\frac{m_{1}}{m}-\frac{3}{10})(V_{1}-V_{2})= 0$,因为$V_{1}≠V_{2}$,所以$\frac{m_{1}}{m}-\frac{3}{10}= 0$,解得$m_{1}= \frac{3}{10}m$,$m_{2}= \frac{7}{10}m$,则王冠中金和银的质量之比$m_{1}:m_{2}= \frac{3}{10}m:\frac{7}{10}m= 3:7$。故选A。
解答：A

答案： 解：设纯金块、纯银块、王冠及重物质量为$m$，密度分别为$\rho_1$、$\rho_2$、$\rho_3$，体积分别为$V_1$、$V_2$、$V_3$，左端拉力力臂为$L_{OD}$，$OB$长为$L$。
由杠杆平衡条件：
纯金块：$(mg - \rho_{水}gV_1)L_{OD}=mg(L + 3cm + 7cm)$ ①
纯银块：$(mg - \rho_{水}gV_2)L_{OD}=mgL$ ②
王冠：$(mg - \rho_{水}gV_3)L_{OD}=mg(L + 3cm)$ ③
① - ②：$\rho_{水}g(V_2 - V_1)L_{OD}=mg×10cm$ ④
③ - ②：$\rho_{水}g(V_2 - V_3)L_{OD}=mg×3cm$ ⑤
④/⑤得：$\frac{V_2 - V_1}{V_2 - V_3}=\frac{10}{3}\Rightarrow V_3=\frac{3}{10}V_1+\frac{7}{10}V_2$ ⑥
设王冠中金、银质量为$m_1$、$m_2$，则$V_3=\frac{m_1}{\rho_1}+\frac{m_2}{\rho_2}$，又$\rho_1=\frac{m}{V_1}$，$\rho_2=\frac{m}{V_2}$，代入得$V_3=\frac{m_1}{m}V_1+\frac{m_2}{m}V_2$ ⑦
⑥⑦联立，结合$m_1 + m_2 = m$，解得$m_1=\frac{3}{10}m$，$m_2=\frac{7}{10}m$，故$m_1:m_2=3:7$。
A

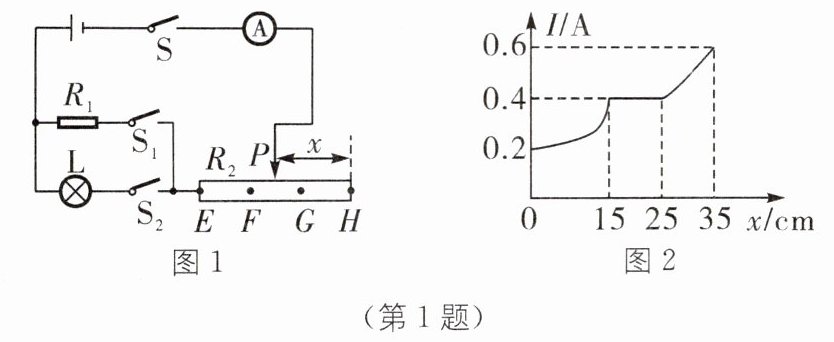
1.(海宁学科素养选拔)如图1所示的电路图中小灯泡标有“2.7V 0.3A”字样,定值电阻$R_{1}= 10Ω$。滑动变阻器$R_{2}$由三段材料不同、横截面积相同的均匀直导体EF、FG、GH连接而成,总长度为35cm,其中一段是铜导体,其电阻可忽略不计,另两段导体的阻值与自身长度成正比,P是与滑动变阻器$R_{2}$接触良好并能移动的滑动触头。只闭合S、$S_{1}$时,电流表示数I与P向左移动距离x之间的关系如图2所示。下列说法正确的是(C)。

(第1题)
A.小灯泡正常发光时电阻为9Ω,电源电压为9V
B.只闭合S、$S_{1}$时,当$x= 15cm$时,电路消耗的总功率为3.6W
C.只闭合S、$S_{2}$,为确保灯丝不被烧坏,滑片P向左移动距离$x≤9cm$
D.只闭合S、$S_{2}$,且确保灯丝不被烧坏,电路消耗的总功率最小为1.8W

答案： 1.C [解析]由题意知当小灯泡两端的电压为2.7 V时，通过小灯泡的电流为0.3 A，小灯泡的电阻$R=\frac{U}{I}=\frac{2.7\,\text{V}}{0.3\,\text{A}}=9\,\Omega$，只闭合S、S₁时，R₁与R₂串联,由图1、图2可知,当滑片在E处时,滑动变阻器R接入电路的阻值为零,此时为R₁的简单电路,电流最大为I=0.6 A,所以电源电压U=IR=0.6 A×10 Ω=6 V,A错误；根据图2可知,当x=15 cm时,电路中的电流为0.4 A,则电路消耗的总功率$P_{\text{总}}=U_{\text{总}}I_{\text{总}}=6\,\text{V}×0.4\,\text{A}=2.4\,\text{W}$,B错误；只闭合S、S₁,由图像可知,当滑片在H点时,电路中的电流为0.2 A,R₁两端的电压$U_1=IR_1=0.2\,\text{A}×10\,\Omega=2\,\text{V}$,R₂的总电阻$R_{2\text{总}}=\frac{U_H}{I}=\frac{U-U_1}{I}=\frac{6\,\text{V}-2\,\text{V}}{0.2\,\text{A}}=20\,\Omega$,滑片P从H端移到E端的过程中,由图像可知GH=15 cm,FG=25 cm-15 cm=10 cm,EF=35 cm-25 cm=10 cm,FG段电流无变化,故FG是铜导体,由图像可知,当滑片P位于F点时,电路中电流$I_F=0.4\,\text{A}$,电路总电阻$R_{\text{总}}'=\frac{U}{I_F}=\frac{6\,\text{V}}{0.4\,\text{A}}=15\,\Omega$,则EF段电阻为$ R_{EF}=R_{\text{总}}'-R_1=15\,\Omega -10\,\Omega=5\,\Omega$,EF导体每1 cm的电阻为$\frac{5\,\Omega}{10\,\text{cm}}=0.5\,\Omega/\text{cm}$,GH导体的电阻$R_{GH}= R_H-R_{EF}=20\,\Omega -5\,\Omega=15\,\Omega$,则GH导体每1 cm的电阻为$\frac{15\,\Omega}{15\,\text{cm}}=1\,\Omega/\text{cm}$,只闭合S、S₂时,小灯泡与R₂串联,当小灯泡正常发光时其两端电压为2.7 V,所以滑动变阻器两端电压$U_2=U-U_L=6\,\text{V}-2.7\,\text{V}=3.3\,\text{V}$,滑动变阻器接入电路的电阻$ R_2=\frac{U_2}{I_{\text{额}}}=\frac{3.3\,\text{V}}{0.3\,\text{A}}=11\,\Omega$,而$R_{EF}=5\,\Omega$,$R_{GH}=15\,\Omega$,则GH段接入电路电阻为11 Ω-5 Ω=6 Ω,未接入电路部分电阻为15 Ω-6 Ω=9 Ω,所以$x\leq\frac{9\,\Omega}{1\,\Omega/\text{cm}}=9\,\text{cm}$,C正确；只闭合S、S₂时,小灯泡与R₂串联,为了保证灯丝不被烧坏,那么通过电路の最大电流为0.3 A,则此时电路的最大功率$P_{\text{大}}=UI_{\text{大}}=6\,\text{V}×0.3\,\text{A}=1.8\,\text{W}$,D错误。