第106页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
12. (2024·呼伦贝尔中考)如图所示,电水壶的规格为“220 V 1210 W”、电热水器的规格为“220 V 2420 W”、电能表上标着“3000 revs/(kW·h)”字样。当电路中单独使用电水壶烧水时,铝盘转动 165 转,用时 180 s;在电路中单独使用电热水器时,用时 6 min。导线、电水壶和电热水器的电阻不随温度变化。求:
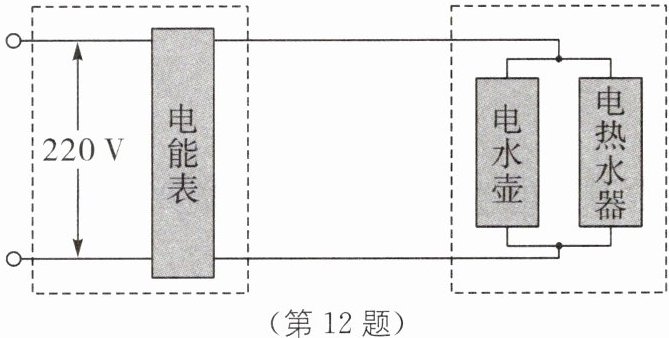
(1)电水壶和电热水器的电阻;
(2)单独使用电热水器时导线上产生的热量。
]

(1)电水壶和电热水器的电阻;
(2)单独使用电热水器时导线上产生的热量。
]
答案:
(1)40Ω 20Ω
(2)1.21×10⁵J
[解析]
(1)根据I=U/R和P=UI,可得R=U²/P,则电水壶的电阻R电水壶=U²/P电水壶=(220V)²/1210W=40Ω,电热水器的电阻R电热水器=U²/P电热水器=(220V)²/2420W=20Ω。
(2)单独使用电水壶烧水时,导线与电水壶串联,电路消耗的电能W=165r/3000r×1kW·h=11/200kW·h,电路的总功率P=W/t=11/200kW·h/0.05h=1.1kW=1100W,电路的总电阻R=U²/P=(220V)²/1100W=44Ω,导线的电阻R线=R−R电水壶=44Ω-40Ω=4Ω,单独使用电热水器时,电路的总电阻R'=R线+R电热水器=4Ω+20Ω=24Ω,电路中的电流I'=U/R'=220V/24Ω=55/6A,导线上产生的热量Q=I'²R线t'=(55/6A)²×4Ω×6×60s=1.21×10⁵J。
(1)40Ω 20Ω
(2)1.21×10⁵J
[解析]
(1)根据I=U/R和P=UI,可得R=U²/P,则电水壶的电阻R电水壶=U²/P电水壶=(220V)²/1210W=40Ω,电热水器的电阻R电热水器=U²/P电热水器=(220V)²/2420W=20Ω。
(2)单独使用电水壶烧水时,导线与电水壶串联,电路消耗的电能W=165r/3000r×1kW·h=11/200kW·h,电路的总功率P=W/t=11/200kW·h/0.05h=1.1kW=1100W,电路的总电阻R=U²/P=(220V)²/1100W=44Ω,导线的电阻R线=R−R电水壶=44Ω-40Ω=4Ω,单独使用电热水器时,电路的总电阻R'=R线+R电热水器=4Ω+20Ω=24Ω,电路中的电流I'=U/R'=220V/24Ω=55/6A,导线上产生的热量Q=I'²R线t'=(55/6A)²×4Ω×6×60s=1.21×10⁵J。
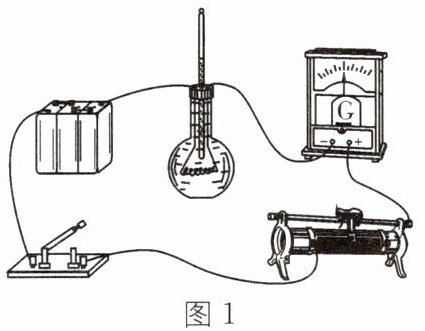
13. 控制变量法 (2023·温州中考)用如图 1 所示电路研究电热与电流的关系,比较不同设定电流值时的电热多少。调节电流大小的过程中,电热丝已经开始加热,因而会影响实验的准确性。为解决这一问题,小明设计了如图 2 所示电路进行研究。
如图 2 所示的电路包含调试电路和实验电路,$R_{1}和R_{2}$是阻值都为 20 Ω的电热丝,$R_{2}$放置在装有煤油的保温容器中。实验中先使用调试电路进行调试,使电热丝$R_{2}$在调试过程中不发热。实验步骤如下。
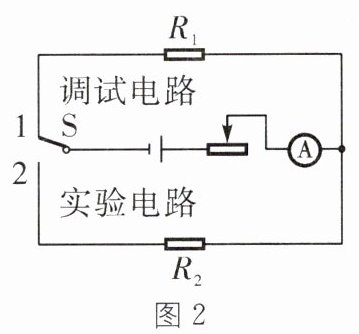
①用数字温度计测量并记录装有$R_{2}$的保温容器内煤油的温度。
②将开关 S 拨至“1”,调节滑动变阻器,直至电流表示数为 0.2 A。
③将开关 S 拨至“2”,使$R_{2}$工作 50 s,断开开关 S,测量并记录 。
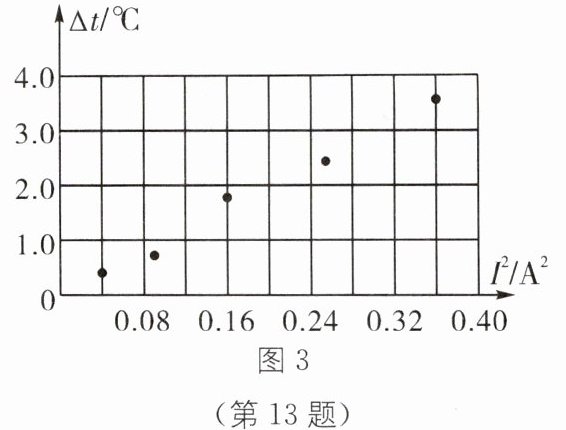
④再将电流值分别设定为 0.3 A、0.4 A、0.5 A、0.6 A,重复上述步骤。记录相关数据,并计算每次升高的温度$\Delta t$($\Delta t$可反映电热的多少),整理$\Delta t$、$I^{2}$的数据如图 3 所示。
(1)将步骤③补充完整。
(2)在图 3 中画出$\Delta t与I^{2}$的关系图像。
(3)小明想改变电热丝阻值,用上述实验中设定的电流值,继续研究电热与电流的关系:保持$R_{1}$不变,将$R_{2}$更换为 30 Ω的电热丝,重复上述步骤。他的做法是否合理,说明理由: 。
如图 2 所示的电路包含调试电路和实验电路,$R_{1}和R_{2}$是阻值都为 20 Ω的电热丝,$R_{2}$放置在装有煤油的保温容器中。实验中先使用调试电路进行调试,使电热丝$R_{2}$在调试过程中不发热。实验步骤如下。



①用数字温度计测量并记录装有$R_{2}$的保温容器内煤油的温度。
②将开关 S 拨至“1”,调节滑动变阻器,直至电流表示数为 0.2 A。
③将开关 S 拨至“2”,使$R_{2}$工作 50 s,断开开关 S,测量并记录 。
④再将电流值分别设定为 0.3 A、0.4 A、0.5 A、0.6 A,重复上述步骤。记录相关数据,并计算每次升高的温度$\Delta t$($\Delta t$可反映电热的多少),整理$\Delta t$、$I^{2}$的数据如图 3 所示。
(1)将步骤③补充完整。
(2)在图 3 中画出$\Delta t与I^{2}$的关系图像。
(3)小明想改变电热丝阻值,用上述实验中设定的电流值,继续研究电热与电流的关系:保持$R_{1}$不变,将$R_{2}$更换为 30 Ω的电热丝,重复上述步骤。他的做法是否合理,说明理由: 。
答案:
(1)煤油的温度
(2)如图所示
(3)不合理,调试电路的电流为设定值时,开关S由“1”拨至“2”,根据欧姆定律可知,通过30Ω电热丝的电流不是设定值,电流发生变化,对实验结果产生影响

[解析]
(1)由电流的热效应可知,电流通过R₂时,会产生热量,煤油吸收其产生的热量,温度升高,因此步骤③为将开关S拨至“2”,使R₂工作50s,断开开关S,测量并记录煤油的温度。
(2)根据Q吸=cmΔt可知,煤油的比热容一定,质量不变,因此煤油吸收的热量与其温度的变化量Δt成正比;根据焦耳定律可知,在电阻和通电时间一定时,电流通过导体产生的热量与I²成正比,由此可知,Δt与I²应成正比例关系,其图像应为一条过原点的直线,由于存在实验误差,则图像如答图所示。
(3)调试电路的电流为设定值时,开关S由“1”拨至“2”,根据欧姆定律可知,通过30Ω电热丝的电流不是设定值,电流发生变化,对实验结果产生影响,故小明的想法是不合理的。
(1)煤油的温度
(2)如图所示
(3)不合理,调试电路的电流为设定值时,开关S由“1”拨至“2”,根据欧姆定律可知,通过30Ω电热丝的电流不是设定值,电流发生变化,对实验结果产生影响

[解析]
(1)由电流的热效应可知,电流通过R₂时,会产生热量,煤油吸收其产生的热量,温度升高,因此步骤③为将开关S拨至“2”,使R₂工作50s,断开开关S,测量并记录煤油的温度。
(2)根据Q吸=cmΔt可知,煤油的比热容一定,质量不变,因此煤油吸收的热量与其温度的变化量Δt成正比;根据焦耳定律可知,在电阻和通电时间一定时,电流通过导体产生的热量与I²成正比,由此可知,Δt与I²应成正比例关系,其图像应为一条过原点的直线,由于存在实验误差,则图像如答图所示。
(3)调试电路的电流为设定值时,开关S由“1”拨至“2”,根据欧姆定律可知,通过30Ω电热丝的电流不是设定值,电流发生变化,对实验结果产生影响,故小明的想法是不合理的。
查看更多完整答案,请扫码查看


