《2025年顶尖课课练七年级数学下册华师大版》

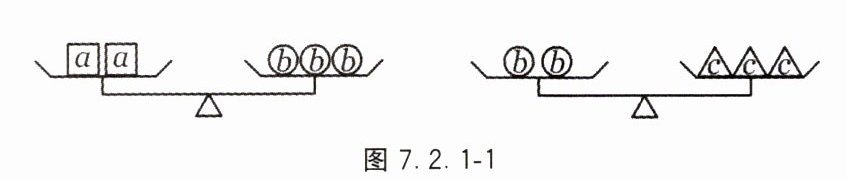
7. 如图7.2.1-1，若两架天平都保持平衡，则关于$a$、$b$、$c$三种物体的质量判断正确的是（ ）.


A. $a＞c$
B. $a＜c$
C. $a＜b$
D. $b＜c$

答案： A

8. 若$-1＜a＜b＜0$，则$-a$、$-b$、$1 - a$、$1 - b$的大小顺序为____________________.（用“＜”连接起来）

答案： $-b ＜ -a ＜ 1 - b ＜ 1 - a$

9. 利用不等式的基本性质说明下列结论的正确性：
（1）若$a＜b$，则$\frac{a + b}{2}＜b$；
（2）已知$a$、$b$、$c$、$d$都是负数，且$a＞b$，$c＞d$，试说明：$ac＜bd$.

答案： 略

10. 根据等式和不等式的性质，可以得到：若$a - b＞0$，则$a＞b$；若$a - b = 0$，则$a = b$.若$a - b＜0$，则$a＜b$；这是利用“作差法”比较两个数或两个代数式值的大小.
（1）已知$A = 5m^{2}-4(\frac{7}{4}m-\frac{1}{2})$，$B = 7(m^{2}-m)+3$，请运用前面介绍的方法比较代数式$A$与$B$的大小；
（2）比较$3a + 2b$与$2a + 3b$的大小.

答案：
(1) $A ＜ B$
(2) 当 $a＞b$ 时，$3a + 2b＞2a + 3b$；当 $a = b$ 时，$3a + 2b = 2a + 3b$；当 $a ＜ b$ 时，$3a + 2b＜2a + 3b$