《2025年高中总复习优化设计高中物理》

1.(多选)(2023海南卷)如图所示，1、2轨道分别是天宫二号飞船在变轨前后的轨道，下列说法正确的是(　　　)
　　　　　　　　
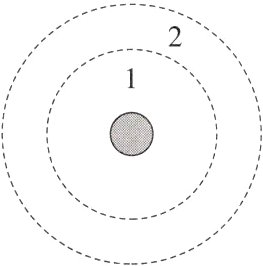
A.飞船从1轨道变到2轨道要点火加速
B.飞船在1轨道的周期大于在2轨道的周期
C.飞船在1轨道的速度大于在2轨道的速度
D.飞船在1轨道的加速度大于在2轨道的加速度

答案： ACD　解析：飞船从较低的轨道1进入较高的轨道2要进行加速做离心运动才能完成，A正确；根据$G\frac{m_{0}m}{r^{2}} = m\frac{v^{2}}{r}=m\frac{4\pi^{2}}{T^{2}}r = ma$，可得$a=\frac{Gm_{0}}{r^{2}}$，$v = \sqrt{\frac{Gm_{0}}{r}}$，$T = 2\pi\sqrt{\frac{r^{3}}{Gm_{0}}}$，可知飞船在轨道1的周期小于在轨道2的周期，在轨道1的速度大于在轨道2的速度，在轨道1的加速度大于在轨道2的加速度，B错误，C、D正确。

2.我国在海南文昌航天发射场，用长征五号遥五运载火箭成功将嫦娥五号探测器送入预定轨道。嫦娥五号在进入环月圆轨道前要进行两次“刹车”，如图所示，第一次“刹车”是在P点让其进入大椭圆轨道，第二次是在P点让其进入环月轨道。下列说法正确的是(　　　)
　　　　　　　　　　　
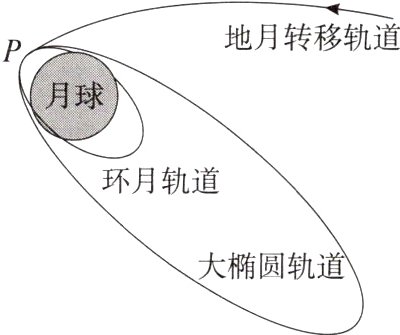
A.探测器在不同轨道上经过P点时所受万有引力相同
B.探测器完成第二次“刹车”后，运行过程线速度保持不变
C.探测器在环月轨道上运行周期比在大椭圆轨道上运行周期大
D.探测器在环月轨道上运动的机械能比在大椭圆轨道上运动的机械能大

答案： A　解析：根据万有引力表达式得$F = G\frac{m_{地}m}{r^{2}}$，可知探测器在不同轨道上经过P点时所受万有引力相同，A正确；探测器完成第二次“刹车”后，做匀速圆周运动，运行过程线速度大小保持不变，方向不断变化，故运行速度是变化的，B错误；因为探测器在环月轨道上运行的轨道半径比在大椭圆轨道上运行的轨道半长轴小，根据开普勒第三定律$\frac{r^{3}}{T^{2}}=k$可知，探测器在环月轨道上运行周期比在大椭圆轨道上运行周期小，C错误；探测器从大椭圆轨道进入环月轨道，做近心运动，故需点火减速，即发动机做负功，机械能减小，故在环月轨道上运动的机械能比在大椭圆轨道上运动的机械能小，D错误。

3.“天舟五号”货运飞船仅用2小时就与“天宫”空间站快速交会对接，创造了世界纪录。飞船从预定轨道Ⅰ的A点第一次变轨进入椭圆轨道Ⅱ，到达椭圆轨道的远地点B时，再次变轨进入空间站的运行轨道Ⅲ，与空间站实现对接，假设轨道Ⅰ和Ⅲ都近似为圆轨道，不计飞船质量的变化，则飞船(　　　)
　　　　　　　　　
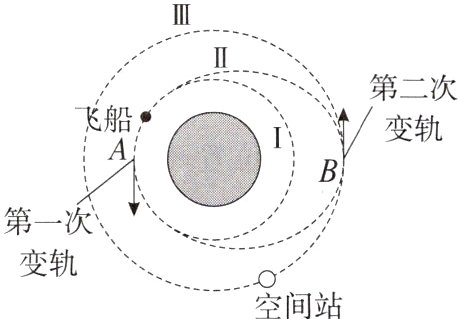
A.在轨道Ⅰ的线速度大于第一宇宙速度
B.在轨道Ⅰ上的运行周期小于空间站的运行周期
C.第一次变轨需加速，第二次变轨需减速
D.在圆轨道Ⅰ上A点与椭圆轨道Ⅱ上A点的加速度不同

答案： B　解析：根据万有引力提供向心力可得$G\frac{m_{0}m}{r^{2}}=m\frac{v^{2}}{r}$，解得$v=\sqrt{\frac{Gm_{0}}{r}}$，地球第一宇宙速度等于卫星在地球表面轨道绕地球做匀速圆周运动的线速度，可知飞船在轨道Ⅰ的线速度小于第一宇宙速度，故A错误；根据万有引力提供向心力可得$G\frac{m_{0}m}{r^{2}}=m\frac{4\pi^{2}}{T^{2}}r$，解得$T=\sqrt{\frac{4\pi^{2}r^{3}}{Gm_{0}}}$，由于轨道Ⅰ的半径小于轨道Ⅲ的半径，则飞船在轨道Ⅰ上的运行周期小于空间站的运行周期，故B正确；卫星从低轨变轨到高轨道，在变轨处都需要点火加速，则第一次变轨需要加速，第二次变轨也需加速，故C错误；根据牛顿第二定律可得$G\frac{m_{0}m}{r^{2}}=ma$，解得$a=\frac{Gm_{0}}{r^{2}}$，由于$m_{0}$、r都相同，则飞船在圆轨道Ⅰ上A点与椭圆轨道Ⅱ上A点的加速度相同，故D错误。

4.天文学家发现了一对被称为“灾变变星”的罕见双星系统，约每51 min彼此绕行一圈，通过天文观测的数据，模拟该双星系统的运动，推测在接下来的7 000万年里，这对双星彼此绕行的周期逐渐减小至18 min。如果将该双星系统简化为理想的圆周运动模型，如图所示，两星球在万有引力作用下，绕O点做匀速圆周运动。不考虑其他天体的影响，两颗星球的质量不变，在彼此绕行的周期逐渐减小的过程中，下列说法正确的是(　　　)
　　　　　　　　　　　
A.每颗星球的角速度都在逐渐变小
B.两颗星球的距离在逐渐变大
C.两颗星球的轨道半径之比保持不变
D.每颗星球的加速度都在变小

答案： C　解析：根据题意，由公式$\omega=\frac{2\pi}{T}$可知，由于彼此绕行的周期逐渐减小，则每颗星球的角速度都在逐渐变大。设双星转动的角速度为$\omega$，双星间距离为L，星球的质量分别为$m_1$、$m_2$，由万有引力提供向心力有$\frac{G m _ { 1 } m _ { 2 }}{L ^ { 2 }}= m _ { 1 } \omega ^ { 2 } r _ { 1 } = m _ { 2 } \omega ^ { 2 } r _ { 2 }$，解得$\omega=\sqrt{\frac{G(m_1 + m_2)}{L^3}}$，可知距离L逐渐变小，故A、B错误；根据题意，由万有引力提供向心力有$\frac{G m _ { 1 } m _ { 2 }}{L ^ { 2 }}= m _ { 1 }\omega ^ { 2 } r _ { 1 }= m _ { 2 }\omega ^ { 2 } r _ { 2 }$，解得$\frac{r_1}{r_2}=\frac{m_2}{m_1}$，由于星球质量不变，则两颗星球的轨道半径之比保持不变，故C正确；由万有引力提供向心力有$\frac{G m _ { 1 } m _ { 2 }}{L^2}= m _{ 1 } a _{ 1 }= m _{ 2 } a _{ 2 }$可知，由于距离L逐渐变小，每颗星球的加速度都在变大，故D错误。

5.如图所示，卫星甲、乙均绕地球做匀速圆周运动，轨道平面相互垂直，乙的轨道半径是甲的$\sqrt[3]{49}$倍。将两卫星和地心在同一直线且甲、乙位于地球同侧的位置称为“相遇”，则从某次“相遇”后，甲绕地球运动15圈的时间内，甲、乙卫星将“相遇”(　　　)
　　　　　　　　　　　
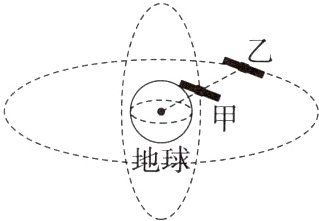
A.1次　　
　B.2次　　　
　C.3次　　　
　D.4次

答案： D　解析：根据开普勒第三定律有$(\frac{r_乙}{r_甲})^3 = (\frac{T_乙}{T_甲})^2$，解得$T_乙 =7 T_甲$，从图示时刻开始，乙转动半圈，甲转动3.5圈，“相遇”一次，此后乙每转动半圈，两个卫星就“相遇”一次，则甲运动15圈的时间内，甲、乙卫星将“相遇”4次，故选D。

6.黑洞是一种密度极大、引力极大的天体，以至于光都无法逃逸，科学家一般通过观测绕黑洞运行的天体的运动规律间接研究黑洞。已知某黑洞的逃逸速度为$v = \sqrt{\frac{2Gm_{0}}{R}}$，其中引力常量为G，$m_{0}$是该黑洞的质量，R是该黑洞的半径。若天文学家观测到与该黑洞相距为r的天体以周期T绕该黑洞做匀速圆周运动，光速为c，则下列关于该黑洞的说法正确的是(　　　)
A.该黑洞的质量为$\frac{4\pi r^{3}}{GT^{2}}$
B.该黑洞的质量为$\frac{4\pi r^{3}}{GT^{2}}$
C.该黑洞的最大半径为$\frac{4\pi^{2}r^{3}}{c^{2}}$
D.该黑洞的最大半径为$\frac{8\pi^{2}r^{3}}{c^{2}T^{2}}$

答案： D　解析：天体绕黑洞运动时，有$G \frac{m _{ 0 } m }{ r ^{ 2 }}= m (\frac{2\pi }{ T }) ^{ 2 } r$，解得$m _{ 0 }=\frac{4\pi ^{ 2 } r ^{ 3 }}{ G T ^{ 2 }}$，A、B错误；黑洞的逃逸速度不小于光速，则有$\sqrt{\frac{2 Gm _{ 0 }}{ R}}\geqslant c$，解得$R\leqslant \frac{2 Gm _{ 0 }}{ c ^{ 2 }}=\frac{8\pi ^{ 2 } r ^{ 3 }}{ c ^{ 2 } T ^{ 2 }}$，C错误，D正确。