《2025年高中总复习优化设计高中物理》

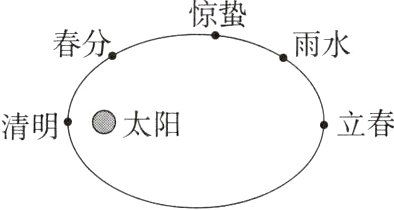
8.（2024福建福州模拟）某国际团队发现了3颗隐藏在太阳强光中的近地小行星，将其中一颗命名为2021PH27。在一年中的前5个节气间该小行星的位置如图所示。已知该小行星近日点到太阳的距离为日地距离的$\frac{2}{15}$，一年近似取360天，可近似认为24个节气在一年内均匀分布。可能用到的数据：$\sqrt[3]{\frac{1}{7}} = 0.52$，$\sqrt[3]{\frac{1}{9}} = 0.48$，$\sqrt[3]{\frac{1}{10}} = 0.46$。则该小行星经过近日点和远日点时的动能之比约为（ ）

A. 1156∶25
B. 169∶5
C. 961∶25
D. 1521∶100

答案： C　解析一年共有24个节气，则相邻节气的间隔约15天，故立春到清明总相差约60天，又小行星2021PH27在椭圆轨道上绕太阳运动，则小行星的运动周期约为120天。小行星2021PH27和地球均绕太阳运动，设小行星轨道的半长轴为a，地球的轨道半径为R，由开普勒第三定律有$\frac{a^{3}}{120^{2}}=\frac{R^{3}}{360^{2}}$，可得$a =\sqrt[3]{\frac{1}{9}} R =0.48 R$，已知该小行星近日点到太阳的距离为日地距离的$\frac{2}{15}$，即$r_{近}=\frac{2}{15}R$，则小行星2021PH27远日点到太阳的距离约为$r_{远}=2a - r_{近}=2×0.48R - \frac{2}{15}R=\frac{62}{75}R$，由开普勒第二定律可知，该小行星经过近日点和远日点时的速度之比为$\frac{v_{近}}{v_{远}}=\frac{r_{远}}{r_{近}}=\frac{31}{5}$，则该小行星经过近日点和远日点时的动能之比约为$\frac{E_{k近}}{E_{k远}}=\frac{\frac{1}{2}mv_{近}^{2}}{\frac{1}{2}mv_{远}^{2}}=\frac{r_{远}^{2}}{r_{近}^{2}}=\frac{961}{25}$，故选C。

9. 假定地球为密度均匀分布的球体，球半径为R。某单摆在地面处做简谐运动的周期T1与在某矿井底部做简谐运动的周期T2之间满足T1=$\sqrt{k}T2$（0＜k＜1）。忽略地球的自转，已知质量均匀分布的球壳对壳内物体的万有引力为零，则该矿井底部离地面的距离为（ ）
A.（1 - k）R
B. (1 - $\frac{1}{\sqrt{k}}$)R
C. kR
D. $\sqrt{k}R$

答案： A　解析球壳部分对物体的万有引力为0，则矿井内重力加速度$g=G\frac{m_{内}}{(R - d)^{2}}$，其中$m_{内}=\rho\cdot\frac{4}{3}\pi(R - d)^{3}$，则$g=\frac{4}{3}\pi\rho G(R - d)$，地面处重力加速度$g_{0}=\frac{4}{3}\pi\rho GR$，则$\frac{g}{g_{0}}=\frac{R - d}{R}$，根据单摆周期公式可知$T_{1}=2\pi\sqrt{\frac{L}{g}}$，$T_{2}=2\pi\sqrt{\frac{L}{g_{0}}}$，且$T_{1}=\sqrt{k}T_{2}$，解得$d=(1 - k)R$，故选A。

10. 已知地球半径为R，月球半径为r，地球与月球之间的距离（两球中心之间的距离）为L。月球绕地球公转的周期为T1，地球自转的周期为T2，地球绕太阳公转周期为T3，假设公转运动都视为圆周运动，引力常量为G，由以上条件可知（ ）
A. 月球运动的加速度为a=$\frac{4\pi^{2}L}{T_{1}^{2}}$
B. 月球的质量为m月=$\frac{4\pi^{2}L}{GT_{1}^{2}}$
C. 地球的密度为ρ=$\frac{3\pi L}{GT_{1}^{2}}$
D. 地球的质量为m地=$\frac{4\pi^{2}L}{GT_{3}^{2}}$

答案： A　解析由月球绕地球做圆周运动有$\frac{Gm_{地}m_{月}}{L^{2}}=m_{月}a=m_{月}\frac{4\pi^{2}}{T^{2}}L$，解得$a=\frac{4\pi^{2}L}{T^{2}}$，故A正确；根据万有引力定律而列出的公式可知月球质量将会约去，所以无法求出，故B错误；由月球绕地球做圆周运动有$\frac{Gm_{地}m_{月}}{L^{2}}=m_{月}\frac{4\pi^{2}}{T^{2}}L$，求得地球质量$m_{地}=\frac{4\pi^{2}L^{3}}{GT^{2}}$，又知体积$V=\frac{4}{3}\pi R^{3}$，则密度为$\rho=\frac{m_{地}}{V}=\frac{3\pi L^{3}}{GT^{2}R^{3}}$，故C、D错误。

11. 同步卫星距地面高度为h，地球表面重力加速度为g，地球半径为R，地球自转周期为T1，近地卫星周期为T2，引力常量为G，则下列关于地球质量及密度表达式正确的是（ ）
A. 地球的质量为$\frac{4\pi^{2}h^{3}}{GT_{1}^{2}}$
B. 地球的质量为$\frac{gR^{2}}{G}$
C. 地球的平均密度为$\frac{3\pi h^{3}}{GT_{1}^{2}R^{3}}$
D. 地球的平均密度为$\frac{3\pi}{GT_{1}}$

答案： B　解析同步卫星周期与地球自转周期相同，为$T_{1}$，则有$G\frac{m_{0}m}{(R + h)^{2}}=m\frac{4\pi^{2}}{T_{1}^{2}}(R + h)$，解得地球质量$m_{0}=\frac{4\pi^{2}(R + h)^{3}}{GT_{1}^{2}}$，则地球的平均密度$\rho=\frac{m_{0}}{V}=\frac{m_{0}}{\frac{4}{3}\pi R^{3}}=\frac{3\pi(R + h)^{3}}{GT_{1}^{2}R^{3}}$，故A、C错误；已知地表重力加速度为g，则近地卫星的向心力为$G\frac{m_{0}m}{R^{2}}=m'g$，可得地球质量$m_{0}=\frac{gR^{2}}{G}$，故B正确；近地卫星的向心力为$G\frac{m_{0}m}{R^{2}}=m\frac{4\pi^{2}}{T_{2}^{2}}R$，地球的平均密度为$\rho=\frac{m_{0}}{V}$，地球的体积为$V=\frac{4}{3}\pi R^{3}$，联立解得地球平均密度为$\rho=\frac{3\pi}{GT_{2}^{2}}$，故D错误。

12.（多选）（2023陕西汉中模拟）将“天问一号”绕火星表面的运动近似看成匀速圆周运动，它的运动周期为T；未来，航天员登陆火星，并在火星表面以大小为v0的速度竖直向上抛出一小球，小球经时间t落回抛出点，不计火星表面的空气阻力。若火星的半径为R，忽略自转的影响，引力常量为G。则下列判断正确的是（ ）
A. 火星表面的重力加速度g=$\frac{v_{0}}{t}$
B. 火星的质量为m0=$\frac{4\pi^{2}R^{3}}{GT^{2}}$
C. 火星的平均密度为ρ=$\frac{3v_{0}}{2\pi GTR}$
D. 火星的第一宇宙速度v=$\sqrt{\frac{2v_{0}R}{t}}$

答案： BD　解析由竖直上抛时间的对称性可知，上升时间为$\frac{t}{2}$，火星表面的重力加速度$g=\frac{v}{\frac{t}{2}}=\frac{2v}{t}$，故A错误；设天问 - 2号的质量为m，由$G\frac{m_{0}m}{R^{2}}=m(\frac{2\pi}{T})^{2}R$，解得$m_{0}=\frac{4\pi^{2}R^{3}}{GT^{2}}$，故B正确；忽略火星自转，质量为m的物体，火星表面重力和万有引力相等，$mg=\frac{Gm_{0}m}{R^{2}}$，得$m_{0}=\frac{gR^{2}}{G}$，火星的平均密度为$\rho=\frac{m_{0}}{\frac{4}{3}\pi R^{3}}=\frac{\frac{gR^{2}}{G}}{\frac{4}{3}\pi R^{3}}=\frac{3v}{2\pi GtR}$，故C错误；由$mg=m\frac{v^{2}}{R}$，解得$v=\sqrt{gR}=\sqrt{\frac{2vR}{t}}$，故D正确。

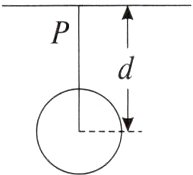
13.（2024北京西城模拟）地质勘探发现某地区表面的重力加速度发生了较大的变化，怀疑地下有空腔区域，进一步探测发现在地面P点的正下方有一球形空腔区域储藏有天然气，如图所示，假设该地区岩石均匀分布且密度为ρ，天然气的密度远小于ρ，可忽略不计，如果没有该空腔，地球表面正常的重力加速度大小为g；由于空腔的存在，现测得P点处的重力加速度大小为kg（k＜1），已知引力常量为G，球形空腔的球心深度为d，则此球形空腔的体积是（ ）

A. $\frac{kgd}{Gρ}$
B. $\frac{kgd^{2}}{Gρ}$
C. $\frac{(1 - k)gd}{Gρ}$
D. $\frac{(1 - k)gd^{2}}{Gρ}$

答案： D　解析如果将近地表的球形空腔填满使密度回到为正$\rho$的常岩石值，因此，如果将空腔填满，地面质量为m的物体的重力为mg，没有填满时是kmg，故空腔填满后引起的引力为$(1 - k)mg$，由万有引力定律有$(1 - k)mg=G\frac{\rho Vm}{d^{2}}$，解得球形空腔的体积$V=\frac{(1 - k)gd^{2}}{G\rho}$，故选D。

14. 某实验小组设计了用单摆测量海底深度的实验。在静止于海底的蛟龙号里，测得摆长为l的单摆，完成N次全振动用时为t。设地球为均质球体，半径为R，地球表面的重力加速度大小为g。已知质量分布均匀的球壳对壳内物体的引力为零。则下列说法正确的是（ ）
A. 此海底处的重力加速度大于地球表面的重力加速度
B. 此海底处的重力加速度为无穷大
C. 此海底处的深度为h=$\frac{4\pi^{2}lN^{2}-gt^{2}}{gt^{2}}R$
D. 此海底处的重力加速度大小为$\frac{4\pi^{2}lN^{2}}{t^{2}}$

答案： D　解析根据万有引力提供重力，在地球表面有$G\frac{m_{0}m}{R^{2}}=mg$，解得$g = G\frac{m_{0}}{R^{2}}=G\frac{\rho\frac{4}{3}\pi R^{3}}{R^{2}}=\frac{4}{3}\pi\rho RG$，已知质量分布均匀的球壳对壳内物体的引力为零，所以此海底处的R减小，重力加速度减小，故A、B错误；根据单摆周期公式$T = 2\pi\sqrt{\frac{l}{g}}$，则此海底处的重力加速度大小为$g=\frac{4\pi^{2}l}{T^{2}}=4\pi^{2}l\cdot(\frac{N}{t})^{2}=\frac{4\pi^{2}lN^{2}}{t^{2}}$，$\frac{g'}{g}=\frac{R'}{R}$，解得$R'=\frac{g'}{g}R=\frac{4\pi^{2}lN^{2}}{gt^{2}}R$，此海底处的深度为$h = R - R'=\frac{gt^{2}-4\pi^{2}lN^{2}}{gt^{2}}R$，故C错误，D正确。