《2025年高中总复习优化设计高中物理》

1. 夏天人们常用蚊香来驱除蚊虫。如图所示，蚊香点燃后缓慢燃烧，若某滑冰运动员（可视为质点）的运动轨迹与该蚊香燃烧的轨迹类似，运动的速率保持不变，则该运动员（ ）

A. 线速度不变
B. 角速度变大
C. 向心加速度变小
D. 运动一圈（360°）所用时间保持不变

答案： B　解析由题意可知线速度大小不变，方向时刻改变，故A错误;运动员运动半径在减小,由$v = \omega r$可知角速度变大,故B 正确;由$a = \frac{v^{2}}{r}$可知，运动半径$r$减小，向心加速度$a$变大，故C错误;一圈的长度逐渐变小，所以运动一圈所用的时间变短，故D错误。

2. 如图是自行车传动结构的示意图，其中大齿轮、小齿轮和后轮的半径分别为$r_1$、$r_2$和$r_3$。假设脚踏板的转速为$n$，则该自行车前进的速度为（ ）

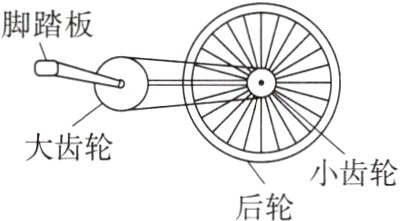
A. $\frac{2\pi nr_2r_3}{r_1}$
B. $\frac{2\pi nr_1r_3}{r_2}$
C. $\frac{2\pi r_1r_3}{nr_2}$
D. $\frac{2\pi r_2r_3}{nr_1}$

答案： B　解析脚踏板的转速等于大齿轮的转速，则大齿轮边缘的线速度$v_{1}=2\pi r_{1}n$，小齿轮边缘的线速度也为$v_{1}=2\pi r_{1}n$，小齿轮和后轮同轴转动,角速度相等,则后轮边缘的线速度即自行车前进的速度为$v_{2}=\frac{v_{1}}{r_{2}}r_{3}=\frac{2\pi nr_{1}r_{3}}{r_{2}}$，故选B。

3. 如图所示，某自行车比赛的赛道可视为圆锥的内表面，路面与铅垂线的夹角为$\alpha$。运动员骑自行车在该赛道上做匀速圆周运动，圆周的半径为$R$，重力加速度为$g$，自行车与路面垂直，不计空气阻力，要使自行车不受摩擦力作用，其速度应等于（ ）

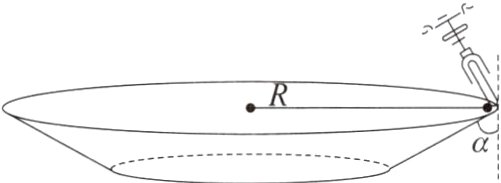
A. $\sqrt{\frac{Rg}{\tan\alpha}}$
B. $\sqrt{Rg\tan\alpha}$
C. $\sqrt{Rg\sin\alpha}$
D. $\sqrt{Rg\cos\alpha}$

答案：
A　解析对自行车进行受力分析，水平方向、竖直方向分别有$F\cos\alpha = m\frac{v^{2}}{R}$，$F\sin\alpha - mg = 0$，解得$v = \sqrt{\frac{Rg}{\tan\alpha}}$，A 正确。
　　　　　　　

4. （2024北京东城区模拟）如图所示，两根长度相同的细线悬挂两个相同的小球，小球在水平面上做角速度相同的匀速圆周运动，已知两细线与竖直方向的夹角分别为$\alpha$和$\beta$，设上下两根细线的拉力分别为$F_1$、$F_2$，则$\frac{F_1}{F_2}$等于（ ）

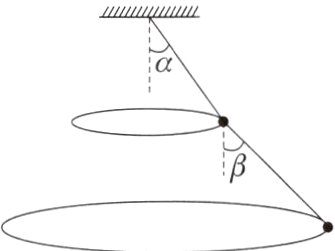
A. $\frac{2\cos\beta}{\cos\alpha}$
B. $\frac{2\cos\alpha}{\cos\beta}$
C. $\frac{2\sin\alpha}{\sin\beta}$
D. $\frac{2\sin\beta}{\sin\alpha}$

答案： A　解析设小球质量为$m$，对下面的小球隔离进行受力分析，小球受重力和下面细线的拉力，做匀速圆周运动，竖直方向受力平衡,则$F_{2}=\frac{mg}{\cos\beta}$，将两个小球看成一个整体进行受力分析,两球受重力和上面细线的拉力,做匀速圆周运动，竖直方向受力平衡,则$F_{1}=\frac{2mg}{\cos\alpha}$，所以$\frac{F_{1}}{F_{2}}=\frac{2\cos\beta}{\cos\alpha}$，故A正确,B、C、D错误。

5. （2023四川南充模拟）有一种能自动计数的智能呼啦圈深受健身者的喜爱，智能呼啦圈腰带外侧有半径$r = 0.12\ m$的圆形光滑轨道，将安装有滑轮的短杆嵌入轨道并能自由滑动，短杆的另一端悬挂一根带有配重的轻质细绳，其简化模型如图所示。已知配重（可视为质点）质量$m = 0.6\ kg$，绳长$L = 0.3\ m$。水平固定好腰带，通过人体微小扭动，使配重在水平面内做匀速圆周运动，在某一段时间内细绳与竖直方向夹角始终为$53^{\circ}$。腰带可看作不动，重力加速度$g$取$10\ m/s^2$，不计空气阻力，$\sin53^{\circ}=0.8$，$\cos53^{\circ}=0.6$，下列说法正确的是（ ）

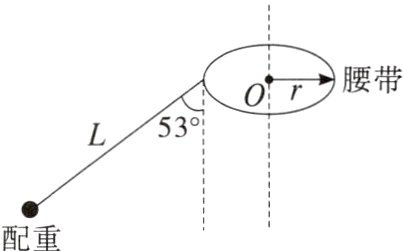
A. 配重受到的合力大小为$10\ N$
B. 配重的角速度为$\omega=\frac{10\sqrt{30}}{9}\ rad/s$
C. 若细绳不慎断裂，配重将自由下落
D. 若增大转速，细绳对配重的拉力将变小

答案： B　解析配重在水平面内做匀速圆周运动,根据牛顿第二定律有$F_{合}=mg\tan53^{\circ}=0.6\times10\times\frac{4}{3}\text{ N}=8\text{ N}$，故A错误;根据牛顿第二定律有$mg\tan53^{\circ}=m\omega^{2}(L\sin53^{\circ}+r)$，解得$\omega=\frac{10\sqrt{30}}{9}\text{ rad/s}$，故B正确;若细绳不慎断裂，配重由于具有切线方向的初速度,配重将做平抛运动,故C错误;若增大转速，即增大角速度,配重做匀速圆周运动的半径增大，细绳与竖直方向的夹角增大，竖直方向根据受力平衡有$F_{T}\cos\theta = mg$，可得$F_{T}=\frac{mg}{\cos\theta}$，可知细绳对配重的拉力将变大，故D错误。

6. 如图所示，足够大水平圆板可绕圆心处的竖直轴以角速度$\omega$匀速转动，圆板上叠放有两物块，下面的大物块质量为$km$，上面的小物块（可视为质点）质量为$m$，小物块和转轴间有一恰好伸直的水平轻绳，轻绳系在套住转轴的光滑小环上，小环被卡在轴上固定高度$h$处，轻绳长度$L = 2h$。已知小物块与大物块、大物块与圆板间的动摩擦因数均为$\mu$，且最大静摩擦力等于滑动摩擦力，重力加速度为$g$，则下列说法不正确的是（ ）

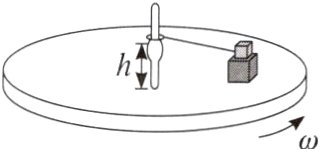
A. $k$越大，大物块发生相对滑动的$\omega$越大
B. 当$k = 1$，$\omega=\sqrt{\frac{\mu g}{h}}$时，大物块未发生相对滑动
C. 当$k = 2$，$\omega=\sqrt{\frac{\mu g}{L}}$时，大物块未发生相对滑动
D. 当$k = 2$，$\omega=\sqrt{\frac{2\mu g}{h}}$时，大物块将会一直做离心运动

答案： A　解析对于大物块，当所受的最大静摩擦力提供向心力时，有$\mu mg+\mu(k + 1)mg=km\omega^{2}L$，解得$\omega=\sqrt{\frac{\mu(k + 2)g}{kL}}=\sqrt{(\frac{2}{k}+1)\frac{\mu g}{L}}$，可知$k$越大，大物块发生相对滑动的$\omega$就越小，A错误;当$k = 1$，$\omega=\sqrt{\frac{\mu g}{L}}$时，大物块所受的最大静摩擦力$F_{fm1}=\mu(k + 2)mg=3\mu mg$，大物块所需要的向心力$F_{n1}=km\omega^{2}L=2\mu mg\lt F_{fm1}$，即大物块不会发生相对滑动，B正确;当$k = 2$，$\omega=\sqrt{\frac{\mu g}{L}}$时，大物块所受的最大静摩擦力$F_{fm2}=\mu(k + 2)mg=4\mu mg$，大物块所需要的向心力$F_{n2}=km\omega^{2}L=2\mu mg\lt F_{fm2}$，即大物块不会发生相对滑动，C正确;当$k = 2$，$\omega=\sqrt{\frac{2\mu g}{L}}$时，大物块所受的最大静摩擦力$F_{fm3}=\mu(k + 2)mg=4\mu mg$，大物块所需要的向心力$F_{n3}=km\omega^{2}L=8\mu mg\gt F_{fm3}$，所以大物块将会发生相对滑动，与小物块脱离之后，摩擦力进一步减小，运动半径继续增大，所以将一直做离心运动，D正确。