《2025年高中总复习优化设计高中物理》

6. (2023山东省实验中学模拟)如图所示，与水平面夹角θ = 30°的传送带正以v = 2 m/s的速度沿顺时针方向匀速运行，A、B两端相距l = 10 m。现每隔1 s把质量m = 1 kg的工件(视为质点)轻放在传送带A端，在传送带的带动下，工件向上运动，工件与传送带间的动摩擦因数μ = $\frac{\sqrt{3}}{2}$，g取10 m/s²，求：
(1)两个工件间的最小距离；
(2)传送带满载时与空载时相比，电机对传送带增加的牵引力。

答案： 答案：
(1)1.2m　
(2)32.5N
解析：
(1)对工件受力分析，根据牛顿第二定律有$\mu mg\cos\theta - mg\sin\theta = ma$。
工件放上传送带后的加速度大小$a = \frac{\mu mg\cos\theta - mg\sin\theta}{m}=2.5m/s^{2}$。
经过$t_1$时间与传送带速度相等，则加速时间、运动距离分别为$t_1 = \frac{v}{a}=0.8s$，$x_1 = \frac{v}{2}t_1 = 0.8m$。
再过$t_2 = 0.2s$，放下一个工件，此时该工件距前一个工件的距离最小，有$x = x_1 + vt_2$。
代入数据解得$x = 1.2m$。
(2)工件与传送带同速后相对静止，在静摩擦力作用下做匀速直线运动直到B端，匀速距离为$l - x_1 = vt_3$。
解得每个工件在传送带上的运动时间$t = t_1 + t_3 = 5.4s$。
当第1个工件刚到达B端时，第6个工件已经在传送带上运动了0.4s，而第7个工件还未放上；传送带上满载时，有1个工件在传送带上滑动，有5个工件相对传送带静止，传送带受到的摩擦力$F_f = \mu mg\cos\theta + 5mg\sin\theta = 32.5N$。
故电机对传送带增加的牵引力$F = F_f = 32.5N$。

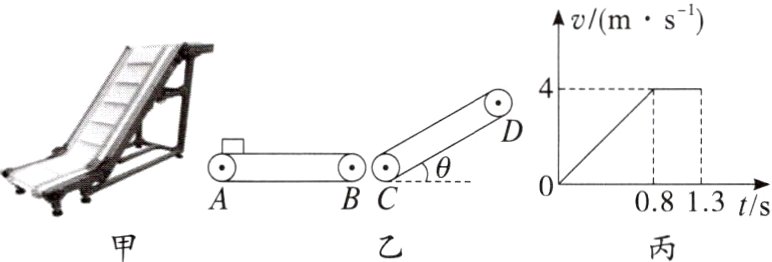
7. (2024广东模拟)图甲是快递分拣传送装置。它由两台传送机组成，一台水平传送，另一台倾斜传送，图乙是该装置示意图，CD部分倾角θ = 37°，B、C间距离忽略不计。已知水平传送带以4 m/s的速率顺时针转动。把一个可视为质点的货物无初速度放在A端，图丙为水平传送带AB段数控设备记录的货物的运动图像，1.3 s时刚好达到B端，且速率不变滑上C端，已知两段传送带的动摩擦因数相同。g取10 m/s²。求：
(1)水平传送带AB的长度及动摩擦因数；
(2)若CD段的长度为2.6 m，则CD部分传送带速度至少为多少，快递员才能在D端取到货物。

答案： 答案：
(1)3.6m　0.5　
(2)3m/s
解析：
(1)由$v - t$图像可知，传送带AB段的长度为$L_{AB}=\frac{1.3 - 0.8 + 1.3}{2}\times4m = 3.6m$。
货物在水平传送带上运动时，根据牛顿第二定律有$\mu mg = ma_1$，解得$a_1 = \mu g$。
由图像可知传送带上的加速过程加速度为$a_1 = \frac{4}{0.8}m/s^{2}=5m/s^{2}$，则$\mu = 0.5$。
(2)依题意，货物以4m/s滑上倾斜传送带CD部分，CD以顺时针方向转动但速度未知。若传送带CD部分速度大于货物速度，不符合传送带速度取最小的情况，故舍弃；若传送带CD部分速度小于货物速度，货物所受摩擦力方向沿斜面向下，则$ma_2 = mg\sin\theta + \mu mg\cos\theta$，解得$a_2 = 10m/s^{2}$。
故货物先沿斜面向上做匀减速直线运动，等到与传送带共速时，由于$\mu＜\tan\theta$，故共速后仍做匀减速直线运动。则$ma_3 = mg\sin\theta - \mu mg\cos\theta$，解得$a_3 = 2m/s^{2}$。
由$s_1 = \frac{v^{2}-4^{2}}{-2a_2}$，$s_2 = \frac{0 - v^{2}}{-2a_3}$，$L_{CD}=s_1 + s_2$，解得$v = 3m/s$。
即传送带的速度至少为3m/s，快递员才能在D端取得货物。