《2025年高中总复习优化设计高中物理》

1.（2023四川雅安模拟）如图所示，传送带以6 m/s匀速率顺时针运动，现将一质量为2 kg的滑块轻放置于传送带的左端，当滑块速度达到6 m/s时，突然断电，传送带以大小为4 m/s²的加速度匀减速运动至停止。已知滑块与传送带间的动摩擦因数为0.2，传送带足够长，重力加速度g取10 m/s²，则滑块从放上去到最后停下的过程中，下列说法正确的是（ ）

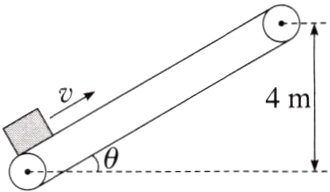
A. 滑块先匀加速后与传送带无相对滑动一起匀减速
B. 滑块受到的摩擦力一直不变
C. 滑块在传送带上留下的划痕为13.5 m
D. 全程滑块与传送带间产生的热量为54 J

答案： D　解析滑块在传送带上先做匀加速直线运动,当达到传送带速度6m/s时,传送带开始匀减速，加速度大小为4m/s²,而滑块的最大加速度为αm=μg=2m/s²＜4m/s²,所以滑块不能和传送带无相对滑动一起匀减速,故A错误;滑块受到传送带的摩擦力一直为滑动摩擦力,但是方向先向右,达到6m/s后摩擦力向左，故B 错误;匀加速阶段,有α=μg=2m/s²,
v=αt1,解得t=3s,所以滑块的位移为x=$\frac{U}{2}$t=$\frac{6}{2}$×3m=9m,传送带的位移为x2=ut1=6×3m=18　m,故在匀加速阶段划痕长度为l=x2　x1=9m,滑块匀减速阶段的加速度大小　　与匀加速阶$\frac{8}{小}$
　段加速度大小相等，且末速度为零，所以匀减速位移的大小与匀加速阶段的位移大小相等,即x1=x=9m,传送带的位移为x2²=2a²=$\frac{62}{2×4}$m=4.5m,故匀减速阶段的划痕长度为l2=x2−x1=
　4.5m＜l,由此可知,滑块在传送带上的划痕长度为9m,故C错误;全过程中摩擦生热为Q=μmgl+μmgl2=54J,故D 正确。

2. 如图所示，绷紧的传送带与水平面的夹角θ = 30°，传送带在电动机的带动下，始终保持1 m/s的速度顺时针运行。现把一质量为5 kg的工件（可视为质点）轻放在传送带的底端，经过一段时间工件与传送带达到共同速度后继续传送到4 m高处。已知工件与传送带间的动摩擦因数为$\frac{\sqrt{3}}{2}$，重力加速度g取10 m/s²，则在此过程中，下列说法正确的是（ ）

A. 工件加速过程的时间为0.8 s
B. 传送带对工件做的功为200 J
C. 工件与传送带间摩擦产生的热量为7.5 J
D. 电动机因传送工件多做的功为120 J

答案： C　解析工件加速过程由牛顿第二定律得μmgcos0−mgsin0=ma,解得加速度α=μgcosθ−gsinθ=2.5m/s²,则加速时间t=$\frac{U}{a}$=0.4s,故A错误;工件在传送带上不仅受重力，还受到传送带对它的摩擦力和支持力,由动能定理有一mgh+W传=$\frac{1}{2}$mv²−0,得传送带对工件做的功W传=$\frac{1}{2}$mu²+mgh=202.5J,故B错误;加速过程工件与传送带相对运动的位移△x=x傅−xI=Ut−$\frac{U}{2}$t=$\frac{1}{2}$t=0.2m,工件与传送带间摩擦产生的热量Q=
　μmgcosθ.x=7.5J,故C正确;电动机多做的功等于系统摩擦产生的热量和工件机械能的增加量,则有W电=Q+$\frac{1}{2}$mu²+mgh=210J,故D错误。

3.（多选）（2024广东惠州模拟）如图所示，质量为m₀、长度为L的小车静止在光滑水平面上，质量为m的小物块（可视为质点）放在小车的最左端，现用一水平恒力F作用在小物块上，使小物块从静止开始做直线运动，当小物块滑到小车的最右端时，小车运动的距离为x，小物块和小车间的滑动摩擦力为Ff，此过程中，下列结论正确的是（ ）

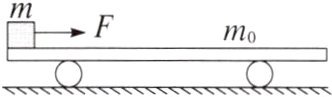
A. 小物块到达小车最右端时，其动能为(F - Ff)(L + x)
B. 摩擦力对小物块所做的功为FfL
C. 小物块到达小车最右端时，小车的动能为Ffx
D. 小物块和小车组成的系统机械能增加量为F(L + x)

答案： AC　解析小物块发生的位移为L÷x，对于小物块根据动能定理可得Ek1=
　(F−Ff)(L+x),故A正确;小物块克服摩擦力做的功为W=Ff(L+x),故B错误;物块到达小车最右端时，小车运动的距离为x,对小车根据动能定理得Ek2=
　Ffx,故C正确;小车和小物块增加的动能为Ek=Ek+Ek2=(F−F)(L+x)+Fx=F(L+x)−FfL,系统重力势能不变，则小物块和小车增加的机槭能为F(L+x)−FL,故D错误。

4. 如图甲所示，长木板A放在光滑的水平面上，质量为m = 2 kg的另一物体B（可看成质点）以水平速度v₀ = 2 m/s滑上原来静止的长木板A的上表面。由于A、B间存在摩擦力，之后A、B速度随时间变化情况如图乙所示。下列说法正确的是（g取10 m/s²）（ ）


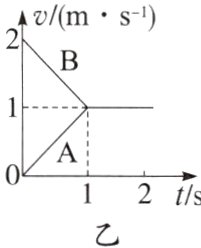
A. 木板A最终获得的动能为2 J
B. 系统损失的机械能为4 J
C. 木板A的最小长度为2 m
D. A、B间的动摩擦因数为0.1

答案： D　解析由题图乙可知,0~1s内,A、B 的加速度大小都为a=1m/s²,物体B和木板A水平方向均受滑动摩擦力,根据牛顿第二定律知二者质量相等，则木板最终动能EkA=$\frac{1}{2}$mv²=1J,选项A错误;系统损失的机械能△E=$\frac{1}{2}$mu。²−$\frac{1}{2}$.2m二耆.相v²对=位2J移，选为项1mB,错即误木;板由A题图的最乙可小得长度为1m,选项C错误;对B受力分析，根据牛顿第二定律,可得μmg=ma,解得μ=0.1,选项D正确。

5. 过山车是游乐场中常见的设施，一种过山车的简易模型如图所示，由弧形轨道AB、竖直圆轨道、水平轨道BCD构成，B是圆轨道的最低点，轨道右端D点处固定有原长为CD的弹簧，BCD段轨道粗糙，其余轨道光滑，各段轨道均平滑连接。用质量m = 1.0 kg的滑块（可视为质点）模拟过山车的运动，现将滑块从与水平轨道之间的高度差为h = 1.8 m位置处静止释放，滑块通过圆轨道后向右运动压缩弹簧，被弹回后第一次到达E点即停止运动。已知滑块与水平轨道BCD之间的动摩擦因数μ = 0.3，BE之间的距离LBE = 2.0 m，EC之间的距离LEC = 1.0 m，滑块始终与圆轨道保持接触，不计空气阻力，重力加速度g取10 m/s²。求：

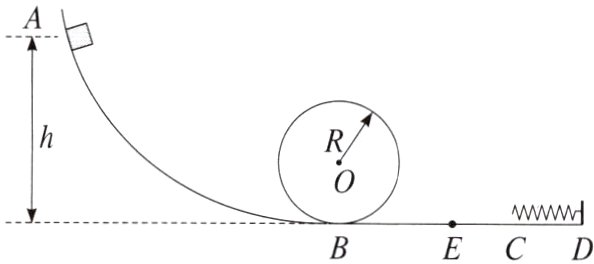
（1）圆轨道半径R的最大值；
（2）弹簧的最大弹性势能。

答案： 答案
(1)0.72m
(2)6
　解析
(1)圆轨道半径R最大时,滑块从圆轨道的最高点经过时对轨道恰好无作用力,设圆轨道半径的最大值为Rmx,在圆轨道的最高点
　　　mg=m$\frac{U}{R}$
　　　滑块从A点运动到圆轨道的最高点，根据动能定理可得
　　　mg(h−2Rmax)=$\frac{1}{2}$mv。²
　　　解得Rmax=0.72m。
(2)滑块从A点运动到B点,根据动能定理可得
　　　mgh=$\frac{1}{2}$mUB²
滑块从B点运动到最右端的过程中，设弹簧的最大压缩量为x,最大弹性势能为Ep,可得
　　　$\frac{1}{2}$mUB²=μmg(LBE+LEc+x)+E。滑块从最右端运动到E点的过程中Ex=μmg(x+LEc)
　　　解得E。=6J。