《2025年高中总复习优化设计高中物理》

1.（2023黑龙江哈尔滨三中二模）如图所示，用OA、OB两根轻绳将花盆悬于两竖直墙之间。开始时OB绳处于水平状态。现保持O点位置不变，只通过改变OB绳长使绳右端由B点缓慢上移至B'点，此时OB'与OA之间的夹角θ＜90°。设此过程中OA、OB绳的拉力分别为F_{OA}、F_{OB}，下列说法正确的是( )

A. F_{OB}先增大后减小
B. F_{OB}先减小后增大
C. F_{OA}先增大后减小
D. F_{OA}先减小后增大

答案：
B　解析 $F_{OA}$、$F_{OB}$ 的合力竖直向上，等于花盆的重力，$OB$ 与 $OA$ 之间的夹角减小的过程中，力三角形如图所示，$F_{OA}$ 逐渐减小，$F_{OB}$ 先减小后增大。故选B。
　　　　　　

2.（多选）如图所示，一根粗糙的水平横杆上套有A、B两个轻环，系在两环上的等长细绳系住的书本处于静止状态，现将两环距离变小后书本仍处于静止状态，则( )

A. 杆对A环的支持力不变
B. B环对杆的摩擦力变小
C. 杆对A环的力不变
D. 与B环相连的细绳对书本的拉力变大

答案： AB　解析 设书本的质量为 $m$，细绳与水平方向的夹角为 $\alpha$，以书本和两环组成的系统为研究对象，根据平衡条件有 $2F_{N}=mg$，解得 $F_{N}=\frac{1}{2}mg$，杆对A环的支持力始终等于书本重力的一半，支持力不变，A正确；对B环根据平衡条件得 $\tan\alpha=\frac{F_{N}}{F_{f}}$，解得 $F_{f}=\frac{mg}{2\tan\alpha}$，将两环距离变小后，$\alpha$ 变大，$\tan\alpha$ 变大，则B环所受杆的摩擦力变小，由牛顿第三定律得，B环对杆的摩擦力变小，B正确；杆对A环的支持力不变，摩擦力变小，则支持力和摩擦力的合力变小，所以杆对A环的力变小，C错误；两细绳的合力等于书本的重力，两环距离变小，两细绳的夹角变小，细绳的拉力变小，D错误。

3. 如图所示，水平面上固定一光滑半球，球心O的正上方固定一个小滑轮，绳上系一小球，小球静置于半球面上的A点时，绳绕过定滑轮，另一端的拉力为F_{T}。现缓慢地将小球从B点释放到A点，则此过程中，小球对半球面的压力F_{N}以及细线拉力F_{T}的大小变化情况，以下说法正确的是( )

A. F_{T}变小；F_{N}不变
B. F_{T}变小；F_{N}变小
C. F_{T}变大；F_{N}不变
D. F_{T}变大；F_{N}变大

答案：
C　解析 对小球受力分析如图所示，由力三角形和几何三角形相似可得 $\frac{F_{N}}{l_{AO}}=\frac{F}{l_{OO'}}=\frac{F_{T}}{l_{O'A}}$，$F = G$，得 $F_{N}=\frac{l_{AO}}{l_{OO'}}G$，$F_{T}=\frac{l_{O'A}}{l_{OO'}}G$，缓慢地将小球从B点释放到A点过程中，$OO'$、$AO$ 不变，$O'A$ 变大，所以 $F_{T}$ 变大，$F_{N}$ 不变，故选C。
　　 　　

4. 课堂上，老师准备了“└”形光滑木板和三个完全相同、外表面光滑的匀质圆柱形积木，要将三个积木按如图所示（截面图）方式堆放在木板上，则木板与水平面夹角θ的最大值为( )

A. 30°
B. 45°
C. 60°
D. 90°

答案： 4.A　解析 $\theta$ 取 $0^{\circ}$ 时，下面两圆柱之间将会分开，无法稳定，应适当增大 $\theta$ 以保持系统稳定，此时下面两圆柱之间有弹力；当下面两圆柱之间的弹力恰好为0时，对应的 $\theta$ 为最小值；继续增大 $\theta$，右圆柱和上圆柱之间弹力减小，若 $\theta$ 太大，此两圆柱将分开，当上圆柱和右圆柱之间的弹力恰好为0，对应的 $\theta$ 为最大值，此时，左边两圆柱的圆心连线在竖直方向上，保证上圆柱只受到两个力的作用处于平衡状态，上圆柱与右圆柱间相互接触且无弹力，可得 $\theta = 30^{\circ}$，A正确，B、C、D错误。

5. 如图所示，重力都为G的两个小球A和B用三段轻绳连接后悬挂在O点上，O、B间轻绳的长度是2l，A、B间轻绳的长度是l。将一个拉力F作用到小球B上，使三段轻绳都伸直，同时O、A间和A、B间的两段轻绳分别处于竖直和水平方向上，则拉力F的最小值为( )

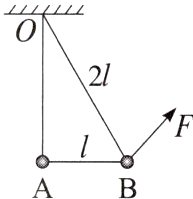
A. $\frac{1}{2}G$
B. $\frac{\sqrt{3}}{3}G$
C. G
D. $\frac{2\sqrt{3}}{3}G$

答案：
5.A　解析 对小球A受力分析可知，因 $O$、A间轻绳竖直，则A、B间轻绳上的拉力为0。对小球B受力分析如图所示，可知当 $F$ 与 $O$、B间轻绳垂直时 $F$ 最小，$F_{min}=G\sin\theta$，其中 $\sin\theta=\frac{l}{2l}=\frac{1}{2}$，则 $F_{min}=\frac{1}{2}G$，故A正确。
　　　　　

6.（2024安徽合肥模拟）如图所示，某校门口水平地面上有一质量为150 kg的石墩，石墩与水平地面间的动摩擦因数为$\frac{\sqrt{3}}{3}$，工作人员用轻绳按图示方式缓慢移动石墩，此时两轻绳平行，重力加速度g取10 m/s²。

(1)若轻绳与水平面的夹角θ为60°，求轻绳对石墩的总作用力大小。
(2)轻绳与水平面的夹角为多大时，轻绳对石墩的总作用力最小？并求出该值。

答案： 答案
(1)$500\sqrt{3}\ N$
(2)$30^{\circ}$ $750\ N$
解析
(1)对石墩受力分析可知 $F\cos60^{\circ}=\mu(mg - F\sin60^{\circ})$ 解得 $F = 500\sqrt{3}\ N$。
(2)由 $F\cos\theta=\mu(mg - F\sin\theta)$ 可得 $F=\frac{\mu mg}{\cos\theta+\mu\sin\theta}=\frac{1500\sqrt{3}}{3\cos\theta+\sqrt{3}\sin\theta}\ N=\frac{1500\sqrt{3}}{2\sqrt{3}(\frac{\sqrt{3}}{2}\cos\theta+\frac{1}{2}\sin\theta)}\ N=\frac{750}{\sin(60^{\circ}+\theta)}\ N$ 则当 $\theta = 30^{\circ}$ 时 $F$ 最小，最小值为 $750\ N$。