《2025年高中总复习优化设计高中物理》

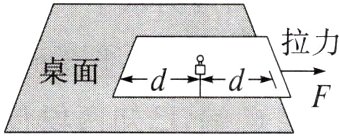
1.（多选）如图所示，将小砝码放在桌面上的薄纸板上，若砝码和纸板的质量分别为$m_0$和$m$，各接触面间的动摩擦因数均为$\mu$，砝码到纸板左端的距离和到桌面右端的距离均为$d$。重力加速度大小为$g$。现用水平向右的恒定拉力$F$拉动纸板，下列说法正确的是( )
　　　　　　　　　　　　　
A. 纸板相对砝码运动时，纸板所受摩擦力的大小为$\mu(m_0 + m)g$
B. 要使纸板相对砝码运动，$F$一定大于$2\mu(m_0 + m)g$
C. 若砝码与纸板分离时的速度小于$\sqrt{\mu gd}$，砝码不会从桌面上掉下
D. 当$F = \mu(2m_0 + 3m)g$时，砝码恰好到达桌面边缘

答案： BC　解析：分析纸板，当纸板相对砝码运动时，纸板所受的摩擦力为μ(m₀ + m)g + μm₀g，A项错误。设砝码的加速度为a₁，纸板的加速度为a₂，则有μm₀g = m₀a₁，F - μm₀g - μ(m₀ + m)g = ma₂，发生相对运动需要a₂＞a₁，代入数据解得F＞2μ(m₀ + m)g，B项正确。若砝码与纸板分离时的速度小于$\sqrt{μgd}$，砝码匀加速运动的位移小于$\frac{v²}{2a₁}=\frac{μgd}{2μg}=\frac{d}{2}$，匀减速运动的位移小于$\frac{v²}{2a₁}=\frac{μgd}{2μg}=\frac{d}{2}$，则总位移小于d，砝码不会从桌面上掉下，C项正确。当F = μ(2m₀ + 3m)g时，砝码未脱离纸板时的加速度a₁ = μg，纸板的加速度a₂ = $\frac{F - μ(m₀ + m)g - μm₀g}{m}$ = 2μg，根据$\frac{1}{2}$a₂t² - $\frac{1}{2}$a₁t² = d，解得t = $\sqrt{\frac{2d}{μg}}$，则此时砝码的速度v = a₁t = $\sqrt{2μgd}$≠0，匀加速运动的位移x = $\frac{1}{2}$a₁t² = d，所以砝码离开桌面，D项错误。

2.（2023山东聊城二模）如图所示，质量$m_0 = 2\ kg$、长度$L = 1.2\ m$的木板A静置在足够大的光滑水平地面上，质量$m = 1\ kg$且可视为质点的物块B放在木板A的右端，现对木板A施加一水平向右的恒力$F = 5\ N$，两者由静止开始运动，作用一段时间$t$后撤去恒力$F$，最终物块B恰好能到达木板A的左端，已知物块B与木板A间的动摩擦因数$\mu = 0.1$，重力加速度$g$取$10\ m/s^2$，求：
　　　　　　　
(1)恒力$F$作用的时间$t$；
(2)摩擦力对物块B做的功$W$。

答案： 答案：
(1)1.2s　
(2)2J
解析：
(1)根据题意，设B的加速度为a₁，力F作用时A的加速度为a₂，撤去力F后A的加速度为a₃，又经过t₁后B达到A的左端，根据牛顿第二定律，有：
μm g = m a₁
F - μm g = m₀ a₂
撤去力F后，根据牛顿第二定律，有μm g = m₀ a₃
由运动学规律得：
a₁(t + t₁) = a₂ t - a₃ t₁
L = $\frac{1}{2}$a₂t² + a₂t t₁ - $\frac{1}{2}$a₃t₁² - $\frac{1}{2}$a₁(t + t₁)²
解得t = 1.2s，t₁ = 0.8s。
(2)设最终B的速度为v，有
v = a₁(t + t₁)
由动能定理有
W = $\frac{1}{2}$mv²
解得W = 2J。

3.（多选）(2024湖北武昌模拟)如图所示，在光滑水平面上，A、B两物体叠放在一起，A放在B的上面，已知$m_A = 4\ kg$，$m_B = 2\ kg$，A、B之间的动摩擦因数$\mu = 0.5$，$g$取$10\ m/s^2$，最大静摩擦力等于滑动摩擦力。对物体A施加水平向右的拉力$F$，开始时拉力$F = 20\ N$，此后逐渐增加，在增大到$50\ N$的过程中，下列说法正确的是( )
　　　
A. 当拉力$F ＜ 30\ N$时，两物体均保持相对静止状态
B. 两物体开始没有相对运动，当拉力超过$30\ N$时，两物体开始相对滑动
C. 两物体间始终没有相对运动
D. 两物体间从受力开始就有相对运动

答案： AC　解析：两物体间达到最大静摩擦力时，对A有F - μmₐg = mₐa，对B有μmₐg = mᵦa，得F = 60N，当F＞60N时，两物体相对滑动；则当拉力F＜30N时，两物体均保持相对静止状态，A正确，B错误；由A、B可知，在F增大到50N的过程中，两物体始终没有相对运动，C正确，D错误。

4. 如图所示，静止在水平地面上的木板(厚度不计)质量为$m_1 = 1\ kg$，与地面间的动摩擦因数$\mu_1 = 0.2$，质量为$m_2 = 2\ kg$且可看成质点的小物块与木板和地面间的动摩擦因数均为$\mu_2 = 0.4$，小物块以$v_0 = 4\ m/s$的水平速度从左端滑上木板，经过$t = 0.6\ s$滑离木板，$g$取$10\ m/s^2$。
　　　　　　　
(1)求木板的长度$L$。
(2)求小物块离开木板时，木板的速度大小。
(3)求小物块离开木板后，木板的加速度。
(4)小物块离开木板后，判断木板与小物块是否发生碰撞。

答案： 答案：
(1)1.32m
(2)1.2m/s
(3)2m/s²，方向水平向左
(4)见解析
解析：
(1)物块在木板上滑动的过程，根据牛顿第二定律，对物块有
μ₂m₂g = m₂a₂
解得a₂ = μ₂g = 4m/s²
对木板有
μ₂m₂g - μ₁(m₁ + m₂)g = m₁a₁
解得a₁ = 2m/s²
木板的长度为
L = (v₀t - $\frac{1}{2}$a₂t²) - $\frac{1}{2}$a₁t²
解得L = 1.32m
(2)小物块离开木板时，木板的速度为
v₁ = a₁t = 1.2m/s。
(3)小物块离开木板后，木板的加速度为a₃ = $\frac{μ₁m₁g}{m₁}$ = μ₁g = 2m/s²，方向水平向左。
(4)小物块离开木板时，物块的速度v₂ = v₀ - a₂t = 1.6m/s
物块在地面上滑行时的加速度大小为a₄ = $\frac{μ₂m₂g}{m₂}$ = μ₂g = 4m/s²
物块在地面上滑行的最大位移为
x₁ = $\frac{v₂²}{2a₄}$ = 0.32m
木板在地面上滑行的最大位移为
x₂ = $\frac{v₁²}{2a₃}$ = 0.36m＞x₁，可知小物块离开木板后，木板与小物块将发生碰撞。