《2025年小题狂做高中物理必修第二册人教版巅峰版》

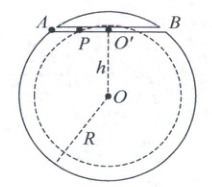
9. (多选,2024 福建期中)某同学设计贯通地球的弦线列车隧道:质量为 m 的列车不需要引擎,从入口的 A 点由静止开始穿过隧道到达另一端的 B 点,O'为隧道的中点,O'与地心 O 的距离为 $h = \frac{\sqrt{3}}{2}R$,地球是半径为 R 的质量均匀分布的球体,地球表面的重力加速度为 g. 已知质量均匀分布的球壳对球内物体引力为 0,P 点到 O'的距离为 x,不计空气阻力与摩擦阻力,忽略地球自转的影响,则 (AC)


A.列车在隧道中 A 点所受的支持力 F = $\frac{\sqrt{3}}{2}mg$
B.列车在隧道中一直做加速运动
C.列车运动到 P 点时的加速度 $a = \frac{x}{R}g$
D.列车运动过程中的最大速度 $v = \sqrt{\frac{1}{2}gR}$

答案：
9. AC 解析:设列车在$A$点时$\angle AOO' =\theta$，列车在$A$点受到地球的引力$F_0 =mg$，列车在$A$点受到的支持力为$F =F_0\cos\theta$，根据几何关系有$\cos\theta =\frac{h}{R}$，联立解得$F =\frac{\sqrt{3}}{2}mg$，A正确;列车在隧道中$AO'O$过程中受到合力水平向右，则列车做加速运动，在$O'B$过程中受到合力水平向左，则列车做减速运动，B错误;设地球的质量为$M$，列车运动到$P$点距地心为$r$，$\angle POO' =\theta'$，根据几何关系有$\sin\theta' =\frac{x}{r}$，列车运动到$P$点的加速度满足$G\frac{M'm}{r^2}·\sin\theta' =ma$，地球为均匀球体，有$\frac{M'}{M}=\frac{r^3}{R^3}$，而$G\frac{Mm}{R^2}=mg$，联立解得$a =\frac{x}{R}g$，C正确;列车在隧道内距$O'$的距离为$x$时合力为$F_合 =\frac{mg}{R}x$，故$F_合$随$x$均匀变化，列车在$O'$点有最大速度，由动能定理，有$\frac{F_A +F_O'}{2}· x_{AO'}=\frac{1}{2}mv^2$，根据几何关系有$x_{AO'} =\sqrt{R^2 -h^2}$，联立解得$v =\frac{1}{2}\sqrt{gR}$，D错误.
思路点拨 因质量均匀分布的球壳对球内物体引力为$0$，则列车运动的过程中它所受万有引力的大小和方向均发生变化，列车在$A$点时受到地球引力和支持力，两个力的合力从$A$指向$B$；列车在$P$点受到地球引力和支持力，引力由半径为$OP$的球体提供；运动到$O'$点时，根据受力分析和牛顿第二定律表示出运动过程的加速度与$x$的关系，再结合动能定理即可求出最大速度.
　　　　　　　

10. (2025 湖南长沙期中)如图所示,半圆轨道 BC 竖直固定在水平地面上,AC 是竖直直径,半径为 R. B 点与圆心 O 等高,轻质弹簧放置在水平地面上,左端固定在距 A 点足够远的地方. 控制质量为 m 的小球(视为质点)向左压缩弹簧至 E 点(未画出),由静止释放小球. 设重力加速度为 g,不计一切摩擦和空气阻力.

(1) 若小球运动到 C 点时所受轨道的弹力大小等于小球重力的 2 倍,求小球经过 C 点的速度大小;
(2) 改变初始时弹簧的压缩量,若小球在半圆轨道运动时不会脱轨(在末端 C 点飞出不算脱轨). 求初始时弹簧弹性势能 $E_p$ 的取值范围;
(3) 若空气阻力不可忽略,且小球所受阻力大小与其速率成正比,即 $f = kv$. k 为已知常数. 若小球恰好通过 C 点,之后小球从 C 点水平飞出,经过时间 t 从 C 点落到水平地面,测得落地点离 C 点的水平距离为 x,求小球从 C 点落到水平地面过程中克服空气阻力做的功 $W_f$. (用 m、R、g、k、t、x 表示结果,表达式合理即可. 不需展开化简)

答案： 10.
(1)在C点，由牛顿第二定律有$3mg=m\frac{v_C^2}{R}$，解得C点的速度大小为$v_C =\sqrt{3gR}$.
(2)若小球刚好能经过圆弧轨道的最高点C，由重力提供向心力有$mg=m\frac{v_{min}^2}{R}$，根据动能定理有$W_1 -2mgR =\frac{1}{2}mv_{min}^2 -0$，解得$E_{p1}=W_1 =2.5mgR$；若小球刚好能运动到圆弧轨道圆心O等高处，根据动能定理有$W_2 -mgR =0$，解得$E_{p2}=W_2 =mgR$.
综上$0＜E_p\leq mgR$或$E_p\geq2.5mgR$.
(3)水平方向，有$-kv_{1x} =m\frac{\Delta v_{1x}}{\Delta t}$，即$-kv_{1x}\Delta t =m\Delta v_{1x}$，即$-k\Delta x_{1x}=m\Delta v_{1x}$，整理可得$-kx =m(v_x -v_{min})$，即$v_x =\sqrt{gR}-\frac{kx}{m}$；同理在竖直方向有$-kv_{1y}+mg =m\frac{\Delta v_{1y}}{\Delta t}$，即$-kv_{1y}\Delta t +mg\Delta t =m\Delta v_{1y}$，整理可得$-ky +mgt =mv_y$，即$v_y =gt -\frac{2kR}{m}$，设落地时速度为$v_2 =\sqrt{v_x^2 +v_y^2}$，由动能定理有$2mgR -W_f =\frac{1}{2}mv_2^2 -\frac{1}{2}mv_{min}^2$，解得$W_f =2.5mgR -\frac{1}{2}m(\sqrt{gR}-\frac{kx}{m})^2 -\frac{1}{2}m(gt -\frac{2kR}{m})^2$.