2025年小题狂做高中物理必修第二册人教版巅峰版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年小题狂做高中物理必修第二册人教版巅峰版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第27页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
6. (北京卷)用频闪照相记录平抛小球在不同时刻的位置,探究平抛运动的特点.
(1) 关于实验,下列做法正确的是
A. 选择体积小、质量大的小球
B. 借助重垂线确定竖直方向
C. 先抛出小球,再打开频闪仪
D. 水平抛出小球
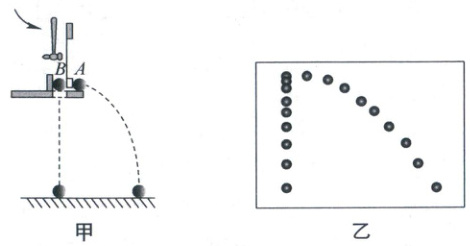
(2) 如图甲所示的实验中,$A$球沿水平方向抛出,同时$B$球自由落下,借助频闪仪拍摄上述运动过程.图乙为某次实验的频闪照片,在误差允许范围内,根据任意时刻$A$、$B$两球的竖直高度相同,可判断$A$球竖直方向做
(3) 某同学使小球从高度为$0.8m$的桌面水平飞出,用频闪照相机拍摄小球的平抛运动(每秒频闪$25$次),最多可以得到小球在空中运动的
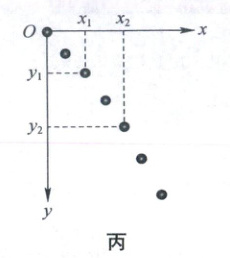
(4) 某同学实验时忘了标记重垂线方向,为解决此问题,他在频闪照片中,以某位置为坐标原点,沿任意两个相互垂直的方向作为$x$轴和$y$轴正方向,建立直角坐标系$xOy$,并测量出另外两个位置的坐标值$(x_{1},y_{1})$、$(x_{2},y_{2})$,如图丙所示.根据平抛运动规律,利用运动的合成与分解的方法,可得重垂线方向与$y$轴间夹角的正切值为
(1) 关于实验,下列做法正确的是
ABD
(填选项前的字母).A. 选择体积小、质量大的小球
B. 借助重垂线确定竖直方向
C. 先抛出小球,再打开频闪仪
D. 水平抛出小球
(2) 如图甲所示的实验中,$A$球沿水平方向抛出,同时$B$球自由落下,借助频闪仪拍摄上述运动过程.图乙为某次实验的频闪照片,在误差允许范围内,根据任意时刻$A$、$B$两球的竖直高度相同,可判断$A$球竖直方向做
自由落体
运动;根据A 球相邻两位置水平距离相等
,可判断$A$球水平方向做匀速直线运动.
(3) 某同学使小球从高度为$0.8m$的桌面水平飞出,用频闪照相机拍摄小球的平抛运动(每秒频闪$25$次),最多可以得到小球在空中运动的
10
个位置.(4) 某同学实验时忘了标记重垂线方向,为解决此问题,他在频闪照片中,以某位置为坐标原点,沿任意两个相互垂直的方向作为$x$轴和$y$轴正方向,建立直角坐标系$xOy$,并测量出另外两个位置的坐标值$(x_{1},y_{1})$、$(x_{2},y_{2})$,如图丙所示.根据平抛运动规律,利用运动的合成与分解的方法,可得重垂线方向与$y$轴间夹角的正切值为
$\frac{|x_{2} - 2x_{1}|}{y_{2} - 2y_{1}}$
.
答案:
6.
(1) ABD
(2) 自由落体 A 球相邻两位置水平距离相等
(3) 10
(4) $\frac{|x_{2} - 2x_{1}|}{y_{2} - 2y_{1}}$
解析:
(1) 用频闪照相记录平抛小球在不同时刻的位置,选择体积小、质量大的小球可以减小空气阻力的影响,A 正确;本实验需要借助重垂线确定竖直方向,B 正确;实验过程先打开频闪仪,再水平抛出小球,C 错误,D 正确.
(2) 根据任意时刻 A、B 两球的竖直高度相同,可以判断出 A 球竖直方向做自由落体运动;根据 A 球相邻两位置水平距离相等,可以判断 A 球水平方向做匀速直线运动.
(3) 小球从高度为$0.8 m$的桌面水平抛出,根据运动学公式$h = \frac{1}{2}gt^{2}$,解得$t = 0.4 s$,频闪仪每秒频闪 25 次,频闪周期$T = \frac{1}{25} s = 0.04 s$,故最多可以得到小球在空中运动的位置个数为$\frac{t}{T} = 10$.
(4) 如图所示,$x_{0}$、$y_{0}$分别表示水平和竖直方向,设重垂线方向$y_{0}$与$y$轴间的夹角为$\theta$,建立坐标系存在两种情况,如图所示,当建立的坐标系为$x_{1}Oy_{1}$时,则$x$轴方向小球做匀减速运动,根据逐差法计算加速度,有$x_{2} - 2x_{1} = -g\sin\theta(2T)^{2}$,$y$轴方向有$y_{2} - 2y_{1} = g\cos\theta(2T)^{2}$,联立解得$\tan\theta = \frac{2x_{1} - x_{2}}{y_{2} - 2y_{1}}$.当建立的坐标系为$x_{2}Oy_{2}$时,则$x$轴方向小球做匀加速运动,根据逐差法计算加速度,有$x_{2} - 2x_{1} = g\sin\theta(2T)^{2}$,$y$轴方向有$y_{2} - 2y_{1} = g\cos\theta(2T)^{2}$,解得$\tan\theta = \frac{x_{2} - 2x_{1}}{y_{2} - 2y_{1}}$.综上所述,重垂线方向与$y$轴间夹角的正切值为$\tan\theta = \frac{|x_{2} - 2x_{1}|}{y_{2} - 2y_{1}}$.

6.
(1) ABD
(2) 自由落体 A 球相邻两位置水平距离相等
(3) 10
(4) $\frac{|x_{2} - 2x_{1}|}{y_{2} - 2y_{1}}$
解析:
(1) 用频闪照相记录平抛小球在不同时刻的位置,选择体积小、质量大的小球可以减小空气阻力的影响,A 正确;本实验需要借助重垂线确定竖直方向,B 正确;实验过程先打开频闪仪,再水平抛出小球,C 错误,D 正确.
(2) 根据任意时刻 A、B 两球的竖直高度相同,可以判断出 A 球竖直方向做自由落体运动;根据 A 球相邻两位置水平距离相等,可以判断 A 球水平方向做匀速直线运动.
(3) 小球从高度为$0.8 m$的桌面水平抛出,根据运动学公式$h = \frac{1}{2}gt^{2}$,解得$t = 0.4 s$,频闪仪每秒频闪 25 次,频闪周期$T = \frac{1}{25} s = 0.04 s$,故最多可以得到小球在空中运动的位置个数为$\frac{t}{T} = 10$.
(4) 如图所示,$x_{0}$、$y_{0}$分别表示水平和竖直方向,设重垂线方向$y_{0}$与$y$轴间的夹角为$\theta$,建立坐标系存在两种情况,如图所示,当建立的坐标系为$x_{1}Oy_{1}$时,则$x$轴方向小球做匀减速运动,根据逐差法计算加速度,有$x_{2} - 2x_{1} = -g\sin\theta(2T)^{2}$,$y$轴方向有$y_{2} - 2y_{1} = g\cos\theta(2T)^{2}$,联立解得$\tan\theta = \frac{2x_{1} - x_{2}}{y_{2} - 2y_{1}}$.当建立的坐标系为$x_{2}Oy_{2}$时,则$x$轴方向小球做匀加速运动,根据逐差法计算加速度,有$x_{2} - 2x_{1} = g\sin\theta(2T)^{2}$,$y$轴方向有$y_{2} - 2y_{1} = g\cos\theta(2T)^{2}$,解得$\tan\theta = \frac{x_{2} - 2x_{1}}{y_{2} - 2y_{1}}$.综上所述,重垂线方向与$y$轴间夹角的正切值为$\tan\theta = \frac{|x_{2} - 2x_{1}|}{y_{2} - 2y_{1}}$.

7. (2024 北京卷)如图所示,水平放置的排水管满口排水,管口的横截面积为$S$,管口离水池水面的高度为$h$,水在水池中的落点与管口的水平距离为$d$.假定水在空中做平抛运动,已知重力加速度为$g$,$h$远大于管口内径.求:
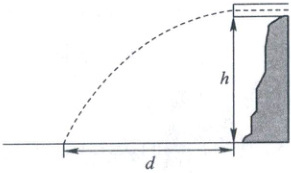
(1) 水从管口到水面的运动时间$t$.
(2) 水从管口排出时的速度大小$v_{0}$.
(3) 管口单位时间内流出水的体积$Q$.

(1) 水从管口到水面的运动时间$t$.
(2) 水从管口排出时的速度大小$v_{0}$.
(3) 管口单位时间内流出水的体积$Q$.
答案:
(1) 水做平抛运动,竖直方向为自由落体运动,由$h=\frac{1}{2}gt^{2}$,解得$t=\sqrt{\frac{2h}{g}}$。
(2) 水平方向为匀速直线运动,由$d=v_{0}t$,将$t=\sqrt{\frac{2h}{g}}$代入,解得$v_{0}=d\sqrt{\frac{g}{2h}}$。
(3) 单位时间内流出水的体积$Q=Sv_{0}$,将$v_{0}=d\sqrt{\frac{g}{2h}}$代入,解得$Q=Sd\sqrt{\frac{g}{2h}}$。
(1)$\sqrt{\frac{2h}{g}}$
(2)$d\sqrt{\frac{g}{2h}}$
(3)$Sd\sqrt{\frac{g}{2h}}$
(1) 水做平抛运动,竖直方向为自由落体运动,由$h=\frac{1}{2}gt^{2}$,解得$t=\sqrt{\frac{2h}{g}}$。
(2) 水平方向为匀速直线运动,由$d=v_{0}t$,将$t=\sqrt{\frac{2h}{g}}$代入,解得$v_{0}=d\sqrt{\frac{g}{2h}}$。
(3) 单位时间内流出水的体积$Q=Sv_{0}$,将$v_{0}=d\sqrt{\frac{g}{2h}}$代入,解得$Q=Sd\sqrt{\frac{g}{2h}}$。
(1)$\sqrt{\frac{2h}{g}}$
(2)$d\sqrt{\frac{g}{2h}}$
(3)$Sd\sqrt{\frac{g}{2h}}$
查看更多完整答案,请扫码查看


