2025年小题狂做高中物理必修第二册人教版巅峰版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年小题狂做高中物理必修第二册人教版巅峰版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第63页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
10. (2025 北京交通大学附属中学开学考)暗物质的研究是目前粒子物理学、天文物理学等学科研究的课题。构建模型研究暗物质,一直是重要的科学思维方法,暗物质与星体间的相互作用遵守万有引力定律。
(1)科学家发现,宇宙中有许多双星系统。双星系统是由两个星体构成,其中每个星体的线度(直径)都远小于两星体间的距离,一般双星系统距离其他星体很远,可以当做孤立系统处理。已知某双星系统中每个星体的质量都是 $ M_0 $,两者相距 $ L $,它们正围绕两者连线的中点做匀速圆周运动,已知引力常量为 $ G $。求:
① 该双星系统的运动的角速度大小 $ \omega $;
② 科学家通过光学实验观测计算得到的角速度大小 $ \omega' $ 与上述①中角速度 $ \omega $ 有些差异,为了解释这个问题,目前有理论认为,在宇宙中可能存在一种观测不到的暗物质可以提供依据。其模型简化为:假定在以这两个星体连线为直径的球体内,均匀分布着密度为 $ \rho $ 的暗物质,不考虑其他星体影响,根据这一模型可以计算该双星系统的运动的角速度 $ \omega' $,试求出角速度大小之比 $ \dfrac{\omega'}{\omega} $。
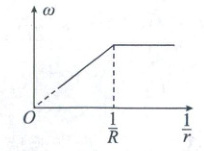
(2)螺旋星系中有大量的恒星和星际物质,主要分布在半径为 $ R $ 的球体内,球体外仅有极少的恒星,球体内物质总质量为 $ M $,可认为均匀分布。且已知球壳对壳内物体的引力为零。球体内外的所有恒星都绕星系中心做匀速圆周运动,恒星到星系中心的距离为 $ r $,科学家根据实测数据,得到此螺旋星系中不同位置的恒星做匀速圆周运动的角速度大小 $ \omega $ 随 $ \dfrac{1}{r} $ 的变化关系如图所示。根据在 $ r > R $ 范围内的恒星运动的 $ \omega $ 与 $ \dfrac{1}{r} $ 成正比,科学家预言螺旋星系周围区域($ r > R $)存在一种暗物质。若暗物质质量均匀分布,请建构模型,估算该区域 $ r = nR $ 内暗物质密度是球体 $ r = R $ 内物质密度的多少倍?
(1)科学家发现,宇宙中有许多双星系统。双星系统是由两个星体构成,其中每个星体的线度(直径)都远小于两星体间的距离,一般双星系统距离其他星体很远,可以当做孤立系统处理。已知某双星系统中每个星体的质量都是 $ M_0 $,两者相距 $ L $,它们正围绕两者连线的中点做匀速圆周运动,已知引力常量为 $ G $。求:
① 该双星系统的运动的角速度大小 $ \omega $;
② 科学家通过光学实验观测计算得到的角速度大小 $ \omega' $ 与上述①中角速度 $ \omega $ 有些差异,为了解释这个问题,目前有理论认为,在宇宙中可能存在一种观测不到的暗物质可以提供依据。其模型简化为:假定在以这两个星体连线为直径的球体内,均匀分布着密度为 $ \rho $ 的暗物质,不考虑其他星体影响,根据这一模型可以计算该双星系统的运动的角速度 $ \omega' $,试求出角速度大小之比 $ \dfrac{\omega'}{\omega} $。
(2)螺旋星系中有大量的恒星和星际物质,主要分布在半径为 $ R $ 的球体内,球体外仅有极少的恒星,球体内物质总质量为 $ M $,可认为均匀分布。且已知球壳对壳内物体的引力为零。球体内外的所有恒星都绕星系中心做匀速圆周运动,恒星到星系中心的距离为 $ r $,科学家根据实测数据,得到此螺旋星系中不同位置的恒星做匀速圆周运动的角速度大小 $ \omega $ 随 $ \dfrac{1}{r} $ 的变化关系如图所示。根据在 $ r > R $ 范围内的恒星运动的 $ \omega $ 与 $ \dfrac{1}{r} $ 成正比,科学家预言螺旋星系周围区域($ r > R $)存在一种暗物质。若暗物质质量均匀分布,请建构模型,估算该区域 $ r = nR $ 内暗物质密度是球体 $ r = R $ 内物质密度的多少倍?

答案:
(1)①对于双星系统,根据万有引力提供向心力,有$G\frac{M_0^2}{L^2} = M_0\omega^2\frac{L}{2}$,可得$\omega = \sqrt{\frac{2GM_0}{L^3}}$。
②设暗物质的质量为m,则$G\frac{M_0^2}{L^2} + G\frac{\rho · \frac{4}{3}\pi(\frac{L}{2})^3M_0}{(\frac{L}{2})^2} = M_0(\omega')^2\frac{L}{2}$,由上式解得$\frac{\omega'}{\omega} = \sqrt{1 + \frac{2\rho\pi L^3}{3M_0}}$。
(2)设球体$r = R$内物质的密度为$\rho$,则$M = \frac{4}{3}\pi R^3\rho$,当$r = R$时,根据$G\frac{Mm}{R^2} = m\omega^2R$,可得$\frac{4}{3}\pi G\rho = \omega^2$,设暗物质密度为$k\rho$,则$G\frac{\frac{4}{3}\pi R^3\rho · m}{(nR)^2} + G\frac{\frac{4}{3}\pi k\rho(nR)^3 · m}{(nR)^2} - G\frac{\frac{4}{3}\pi \rho R^3· m}{(nR)^2} = m\omega_1^2nR$,由题图可知$\omega_1 = \frac{1}{n}\omega$,解得$k = \frac{n - 1}{n^3 - 1}=\frac{1}{n^2 + n + 1}$,即该区域$r = nR$内暗物质密度是球体$r = R$内物质密度的$\frac{1}{n^2 + n + 1}$倍。
(1)①对于双星系统,根据万有引力提供向心力,有$G\frac{M_0^2}{L^2} = M_0\omega^2\frac{L}{2}$,可得$\omega = \sqrt{\frac{2GM_0}{L^3}}$。
②设暗物质的质量为m,则$G\frac{M_0^2}{L^2} + G\frac{\rho · \frac{4}{3}\pi(\frac{L}{2})^3M_0}{(\frac{L}{2})^2} = M_0(\omega')^2\frac{L}{2}$,由上式解得$\frac{\omega'}{\omega} = \sqrt{1 + \frac{2\rho\pi L^3}{3M_0}}$。
(2)设球体$r = R$内物质的密度为$\rho$,则$M = \frac{4}{3}\pi R^3\rho$,当$r = R$时,根据$G\frac{Mm}{R^2} = m\omega^2R$,可得$\frac{4}{3}\pi G\rho = \omega^2$,设暗物质密度为$k\rho$,则$G\frac{\frac{4}{3}\pi R^3\rho · m}{(nR)^2} + G\frac{\frac{4}{3}\pi k\rho(nR)^3 · m}{(nR)^2} - G\frac{\frac{4}{3}\pi \rho R^3· m}{(nR)^2} = m\omega_1^2nR$,由题图可知$\omega_1 = \frac{1}{n}\omega$,解得$k = \frac{n - 1}{n^3 - 1}=\frac{1}{n^2 + n + 1}$,即该区域$r = nR$内暗物质密度是球体$r = R$内物质密度的$\frac{1}{n^2 + n + 1}$倍。
查看更多完整答案,请扫码查看


