《2025年小题狂做高中物理必修第二册人教版巅峰版》

1. (2025山东名校联盟校际联考)山东省是农业大省,已广泛使用无人机进行农作物的监测和喷洒.某次监测无人机(可视为质点)在飞行过程中,水平方向的速度$v_{x}$与飞行时间$t$的关系如图甲所示,竖直方向以$1.5m/s$的速度向上做匀速直线运动,关于无人机的运动,下列说法正确的是(B)


A.$0\sim 1s$内无人机的位移大小为$1.875m$
B.$1s$末无人机的加速度大小为$0.75m/s^{2}$
C.$1s$末无人机的速度大小为$\frac{3\sqrt{5}}{2}m/s$
D.无人机的运动轨迹是图乙中的抛物线$P$

答案： 1.B 解析：由图甲可知，无人机水平方向加速度$a = \frac{\Delta v_x}{\Delta t}=0.75m/s^2$，$0\sim1s$内无人机的水平位移为$x = \frac{1}{2}at_1^2 = 0.375m$，$0\sim1s$内无人机的竖直位移为$y = v_yt_1 = 1.5m$，$0\sim1s$内无人机的位移为$s = \sqrt{x^2 + y^2} \approx 1.55m$，故A错误；无人机的加速度一直不变，故$1s$末无人机的加速度大小为$0.75m/s^2$，故B正确；$1s$末无人机的水平方向速度大小为$v_x = at_1 = 0.75m/s$，$1s$末无人机的速度大小为$v = \sqrt{v_x^2 + v_y^2} = \frac{3\sqrt{5}}{4}m/s$，故C错误；因无人机具有$x$轴正方向的加速度，故合力沿$x$轴正方向，轨迹的弯曲方向指向合力方向，无人机的运动轨迹是图乙中的抛物线$Q$，故D错误.

2. (多选,2024河北石家庄二中期未)如图1、图2所示,一根长为$L$的轻杆$OA$,$O$端用铰链固定于地面,另一端固定着一小球$A$,图1中的小球$A$和图2中的杆分别贴靠着棱长为$a$和$b$的立方块,当立方块沿地面向右滑动到图示位置(杆与地面夹角为$\alpha$)时,速度为$v$,则图1中小球的速度大小$v_{A}$和图2中小球的速度大小$v'_{A}$应为(BC)

A.$v_{A}=v\sin\alpha$
B.$v_{A}=\frac{v}{\sin\alpha}$
C.$v'_{A}=\frac{Lv}{b}\sin^{2}\alpha$
D.$v'_{A}=\frac{Lv}{b}$

答案： 2.BC 解析：图1中，小球与立方体在分离之前，小球在立方体上的接触点位置不断下移，实际上观察到的是小球在与立方体接触过程中做圆周运动，将小球的线速度$v_A$沿水平方向与竖直方向分解，水平方向的分速度等于立方体的速度，则有$v_A\sin\alpha = v$，解得$v_A = \frac{v}{\sin\alpha}$，故A错误，B正确；图2中，立方体向右运动过程中，立方体与杆的接触位置不断发生变化，实际上观察到的是立方体接触过程中向右运动，将立方体的速度$v$沿杆与垂直于杆方向分解，垂直于杆方向的分速度等于杆上接触点做圆周运动的线速度$v_1$，则有$v\sin\alpha = v_1$，小球与杆上接触点做圆周运动的角速度相等，则有$\omega = \frac{v_1}{b} = \frac{v_A'}{L}$，解得$v_A' = \frac{Lv}{b}\sin^2\alpha$，故C正确，D错误.

3. (2024湖南三湘名校教育联盟期中)湖南省进入雨季时,有救援队要在河道里进行救援,救援小组在某次救援时,船由河岸的$A$点出发,经过一段时间到达对岸,已知水流速度为$v_{1}$,船在静水中的速度为$v_{2}$,两河岸的最近距离为$d$,可认为河水的水面是水平的.下列说法正确的是(C)

A.船到达对岸时的速度一定不等于$v_{2}$
B.若$v_{1}＞v_{2}$,船渡河的最小位移为$\frac{\sqrt{v^{2}_{1}+v^{2}_{2}}}{v_{1}}d$
C.若$v_{2}＞v_{1}$,且船渡河的位移最短时,船渡河的时间为$\frac{d}{\sqrt{v^{2}_{2}-v^{2}_{1}}}$
D.船渡河的最短时间为$\frac{d}{\sqrt{v^{2}_{1}+v^{2}_{2}}}$

答案： 3.C 解析：欲使船到达正对岸，则船的速度应斜向上指向上游，使得合速度垂直河岸，此时应有$v_1 ＜ v_2$，合速度大小为船到达对岸时的速度，与$v_2$的大小关系不确定，A错误；若$v_1 ＞ v_2$，合速度方向不可能垂直于河岸，即不可能垂直渡河，当合速度的方向与船的速度方向垂直时，渡河位移最短，设此时合速度的方向与河岸的夹角为$\theta$，有$\sin\theta = \frac{v_1}{v_2}$，则渡河的最小位移$x = \frac{d}{\sin\theta} = \frac{d v_2}{v_1}$，B错误；若$v_2 ＞ v_1$，船渡河的位移最短时，船渡河的时间为$t = \frac{d}{\sqrt{v_2^2 - v_1^2}}$，C正确；欲使船的渡河时间最短，则船的速度方向垂直河岸，渡河的最短时间为$t = \frac{d}{v_2}$，D错误.

4. (2024重庆北碚期末)某工厂两根相同且水平放置的排污管甲和乙(如图所示)正在向外满口排出大量污水,巡查工作人员测量发现甲、乙两排污管离水面的高度之比为$4:1$,落点$A$和$B$离排污口的水平距离之比为$3:4$,忽略空气阻力,甲、乙两管的流量分别为$Q_{1}$、$Q_{2}$(单位时间内排出的污水体积),则(C)


A.甲、乙两管中的污水排出后,在空中的运动时间之比为$4:1$
B.甲、乙两管中的污水排出时,水平速度之比为$3:2$
C.甲、乙两管的流量$Q_{1}$、$Q_{2}$之比为$3:8$
D.排污稳定时,甲、乙两管在空中的污水体积之比为$4:3$

答案： 4.C 解析：平抛物体在竖直方向上做自由落体运动，根据$h = \frac{1}{2}gt^2$，解得$t = \sqrt{\frac{2h}{g}}$，由于甲、乙两排污管离水面的高度之比为$4:1$，则甲、乙两管中的污水排出后，在空中的运动时间之比为$2:1$，A错误；平抛运动在水平方向上做匀速直线运动，根据$x = v_0t$，解得$v_0 = x\sqrt{\frac{g}{2h}}$，由于排污管离水面的高度之比为$4:1$，落点A和B离排污口的水平距离之比为$3:4$，则可得水平速度之比为$3:8$，B错误；由于流量指单位时间内排出的污水体积，甲、乙两根排污管相同，设其横截面积为$S$，则$Q = \frac{Sv_0\Delta t}{\Delta t} = Sv_0$，可知流量之比等于初速度之比，结合上述可知甲、乙两管的流量$Q_1$、$Q_2$之比为$3:8$，C正确；在空中的污水体积$V = Qt$，由于$t = \sqrt{\frac{2h}{g}}$，解得$V = Q\sqrt{\frac{2h}{g}}$，结合上述分析可知，排污稳定时，甲、乙两管在空中的污水体积之比为$3:4$，D错误.

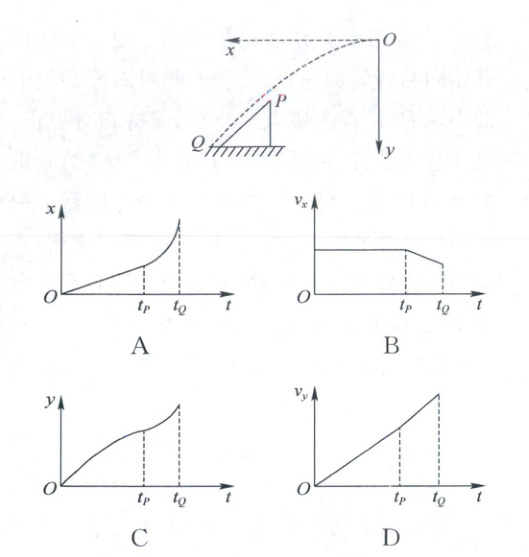
5. (2024广东清远期末)如图所示,将一小物块从坐标原点$O$开始,以某一水平速度沿水平$x$轴向一光滑斜面抛出,物块运动至斜面顶端$P$处时速度恰好与斜面平行,并沿斜面滑下,不计空气阻力,物块可视为质点.物块的位移$x$、$y$和速度$v_{x}$、$v_{y}$随时间$t$变化的图像,可能是下图中的(A)

答案： 5.A 解析：小物块到达斜面之前做平抛运动，水平方向为匀速直线运动，有$x = v_0t$，$v_x = v_0$，竖直方向为自由落体运动，有$y = \frac{1}{2}gt^2$，$v_y = gt$，物块落到斜面之后，受到重力和支持力作用，合力沿斜面向下，设斜面倾角为$\alpha$，根据牛顿第二定律可知$a = g\sin\alpha$，根据平行四边形定则，将加速度分解为水平方向和竖直方向，有$a_x = g\sin\alpha · \cos\alpha$，$a_y = g\sin\alpha · \sin\alpha$，水平方向做匀加速直线运动，竖直方向继续做匀加速直线运动，位移—时间图像的切线斜率表示速度，水平速度先是不变，后逐渐变大，A正确；水平速度先不变，后逐渐变大，所以速度—时间图像先是平行于时间轴，后是向上倾斜的直线，B错误；位移—时间图像的切线斜率表示速度，竖直方向的速度一直增大，所以斜率一直变大，C错误；竖直方向的加速度先是$g$，后小于$g$，速度—时间图像的切线斜率表示加速度，后一阶段的斜率应小于前一阶段的斜率，D错误.