《2025年小题狂做高中物理必修第二册人教版巅峰版》

5. (多选,2024 山西大同一中期中)如图所示为跑车尾翼功能示意图,当汽车高速行驶时,气流会对跑车形成一个向下的压力,压力大小与车速的关系满足$F_{N} = kv^{2}(k = 1.2\ kg/m)$.现某跑车在水平转弯中测试其尾翼功能.当测试车速为$90\ km/h$,未安装尾翼时,其转弯时的最小半径为$90\ m$;当安装尾翼后,转弯时的最小半径可减为$85\ m$.若汽车受到的最大静摩擦力为其对地面压力的$\mu$倍,尾翼质量可以忽略.下列选项中正确的是(AC)


A.$\mu = \dfrac{25}{36}$
B.以上数据无法计算汽车质量
C.未安装尾翼时,若提高汽车转弯速度,则其转弯时的最小半径需增大
D.安装与未安装尾翼相比,车均以相应最小半径转弯时,其向心加速度大小相等

答案： 5.AC 解析：未安装尾翼时$\mu mg=m\frac{v^2}{r_1}$，安装尾翼后$\mu(mg+F_N)=m\frac{v^2}{r_2}$，解得$m=1275 kg$，$\mu=\frac{25}{36}$，A正确，B错误；未安装尾翼时，由$\mu mg=m\frac{v^2}{r_1}$可知，若提高汽车转弯速度，则其转弯时的最小半径需增大，C正确；安装与未安装尾翼时，车均以相应最小半径转弯时，其向心加速度大小为$a=\frac{v^2}{r}$，安装与未安装尾翼相比，转弯的最小半径不同，所以向心加速度不同，D错误.

6. (2024 北京丰台期末)斜抛物体的运动轨迹是一条抛物线,抛物线各个位置的弯曲程度虽然不同,但我们可将抛物线分割成许多很短的小段,即物体在每小段的运动都可以看成半径为某个合适值$\rho$($\rho$称为曲率半径)的圆周运动的一部分,进而采用圆周运动的分析方法来进行研究.如图所示,一个小球被斜向上抛出,初速度方向与水平方向成$\theta$角,抛出点的曲率半径为$\rho_{0}$,重力加速度为$g$,忽略空气阻力,下列说法正确的是(B)

A.初速度大小为$\sqrt{\rho_{0}g\sin\theta}$
B.初速度大小为$\sqrt{\rho_{0}g\cos\theta}$
C.最高点的曲率半径为$\rho_{0}\sin^{3}\theta$
D.最高点的曲率半径为$\rho_{0}\cos^{2}\theta$

答案： 6.B 解析：抛出时，可以把小球的运动看成是半径为$\rho_0$的圆周运动，由牛顿第二定律，有$mg\cos\theta=m\frac{v^2}{\rho_0}$，可得$v=\sqrt{\rho_0g\cos\theta}$，A错误，B正确；在斜抛运动最高点，小球的速度为$v_t=v\cos\theta$，可以把小球的运动看成是半径为$\rho$的圆周运动，又小球只受重力，由牛顿第二定律，有$mg=\frac{mv_t^2}{\rho}$，联立可得$\rho=\rho_0\cos^3\theta$，C、D错误.

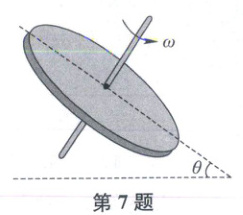
7. (2024 山东烟台期末)如图所示,半径为$R$的匀质实心圆盘.盘面与水平面的夹角为$\theta$,开始时圆盘静止.其上表面均匀覆盖着一层细沙没有掉落,细沙与盘面间的动摩擦因数为$\mu$,设最大静摩擦力等于滑动摩擦力.现让圆盘绕垂直于盘面的固定对称轴旋转,其角速度从$0$开始缓慢增加到$\omega$(未知).此时圆盘表面上的细沙有$\dfrac{8}{9}$被甩掉,重力加速度为$g$,则$\omega$的值为(D)

A.$\sqrt{\dfrac{g(\mu\cos\theta + \sin\theta)}{R}}$
B.$\sqrt{\dfrac{g(\mu\cos\theta - \sin\theta)}{R}}$
C.$\sqrt{\dfrac{3g(\mu\cos\theta + \sin\theta)}{R}}$
D.$\sqrt{\dfrac{3g(\mu\cos\theta - \sin\theta)}{R}}$

答案： 7.D 解析：根据向心力公式$F_n=m\omega^2r$可知，在角速度相同的情况下半径越大，向心力越大，所以最外边的细沙随着角速度的增大最先发生滑动，因为圆盘表面上的细沙有$\frac{8}{9}$被甩掉，即$\frac{8}{9}$面积上的细沙发生滑动，剩下$\frac{1}{9}$的未滑动，设未滑动的半径为$r$，则$\pi r^2=\frac{1}{9}\pi R^2$，解得$r=\frac{1}{3}R$.在最低点，由牛顿第二定律，有$mg(\mu\cos\theta-\sin\theta)=m\omega^2r$，解得$\omega=\sqrt{\frac{3g(\mu\cos\theta-\sin\theta)}{R}}$，故D正确.

8. (2024 江苏南京检测)半径为$R$的光滑水平玻璃圆桌以周期$T$匀速转动,一小球从桌边对准圆心以速度$v = \dfrac{4R}{T}$匀速通过桌面,则小球在桌面留下的痕迹可能是(C)

答案：
8.C 解析：小球通过桌面的时间$t=\frac{2R}{v}=\frac{T}{2}$，故小球运动到正对面时桌面刚好转过半圈，因而痕迹是封闭的，B、D错误；由于玻璃圆桌和小球均在运动，而小球在桌面留下的痕迹其实是小球相对圆桌的运动轨迹，取桌面为参考系，刚出发时，小球相对桌面有指向圆心的速度，同时还有沿桌边切线方向的速度，因此小球出发时应当相对桌面“斜着”走，轨迹不可能是个圆，故C正确，A错误.
思路点拨 做某些复杂的选择题，有时可以采用某些特殊方法，比如本题需要面对图像问题，不需要分析完整的图像痕迹是怎样的，只要找到一些特殊点加以分析，或者抓住关键点就可以排除错误选项，得出答案.
另解1：本题也可以根据轨迹方程来判断.
以桌面为参考系，根据小球速度的特点，前$\frac{T}{4}$内，小球同时参与了两个分运动：向着圆心的匀速直线运动和匀速圆周运动.其合运动为半径随时间均匀减小的近心运动.轨迹方程为$x^2+y^2=(R-vt)^2$；第$\frac{T}{4}$末到达圆桌中心，随后的$\frac{T}{4}$内的运动与刚才的过程相反，小球远离圆心，合运动为离心运动，轨迹方程为$x^2+y^2=(vt)^2$.第$\frac{T}{2}$末，刚好与入射时圆桌边缘的出发点重合，随后飞离圆桌，故应选C.
另解2：本题还可以采用描点法.
以圆桌为参考系，在圆桌上画若干个等间距的同心圆，再以圆心为起点向外画若干条直线，且相邻夹角相等.间隔数与同心圆间隔数相等，描出对应的交点连线即为所求轨迹.如图所示.
　　　　　　

9. (2024 河南百师联盟大联考)在“探究平抛运动特点”的实验中:

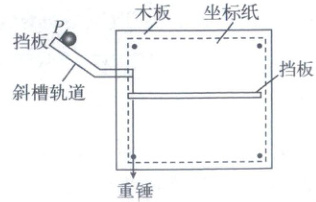
(1)用如图所示装置探究平抛运动分运动的特点.将坐标纸和复写纸对齐重叠并固定在竖直木板上,小球沿斜槽轨道滑下后从斜槽末端飞出,落在水平挡板上.由于挡板靠近木板一侧较低,小球落在挡板上时,会在坐标纸上挤压出一个痕迹点.上下移动挡板,依次重复上述操作,坐标纸上将留下一系列痕迹点.下列说法正确的是(AC)
A. 通过调节使斜槽末端保持水平
B. 挡板高度应等间距变化
C. 不改变挡片$P$的位置,使小球从斜槽上相同位置静止释放
D. 将坐标纸上确定的点用直线依次连接
(2)取下坐标纸(小方格的边长$l = 2.5\ cm$),坐标纸上记录了小球的轨迹,小球以同一初速度平抛运动的几个位置如图中的$a$、$b$、$c$、$d$所示,重力加速度$g$取$10\ m/s^{2}$,则小球在$b$点的瞬时速度的大小为$v_{b} = $$1.25$$m/s$,若以$a$点为坐标原点$(0,0)$,水平向右为$x$轴正方向,竖直向下为$y$轴正方向,小球抛出点的坐标$x = $$-2.5$$cm$,$y = $$-0.3125$$cm$.

答案： 9.
(1)AC
(2)$1.25$ $-2.5$ $-0.3125$
解析：
(1)通过调节使斜槽末端保持水平，以保证小球做平抛运动，故A正确；挡板高度不一定要等间距变化，故B错误；不改变挡片$P$的位置，使小球从斜槽上相同位置静止释放，以保证小球到达底端时速度相同，故C正确；将坐标纸上确定的点用平滑的曲线依次连接，故D错误.
(2)小球做平抛运动，由图可知$a$到$b$与$b$到$c$的水平位移相同，时间间隔相等，设为$T$.竖直方向有$\Delta y=2l-l=gT^2$，解得$T=0.05 s$，水平方向有$v_0=\frac{2×2.5 cm}{0.05 s}=1.0 m/s$，小球在$b$点时竖直方向的分速度$v_y=\frac{3l}{2T}=\frac{3×2.5 cm}{2×0.05 s}=0.75 m/s$，小球在$b$点的速度$v_b=\sqrt{v_0^2+v_y^2}=1.25 m/s$.小球运动到$b$点的时间为$t=\frac{v_y}{g}=\frac{0.75}{10} s=0.075 s$，小球运动到$b$点时，竖直方向的位移为$y'=\frac{1}{2}gt^2$，解得$y'=0.028125 m=2.8125 cm$，小球运动到$b$点时，水平方向的位移为$x'=v_0t$，解得$x'=1×0.075 m=7.5 cm$，若以$a$点为坐标原点，则抛出点的横坐标为$x=2×2.5 cm-7.5 cm=-2.5 cm$，抛出点的纵坐标为$y=2.5 cm-2.8125 cm=-0.3125 cm$.