《2025年小题狂做高中物理必修第二册人教版巅峰版》

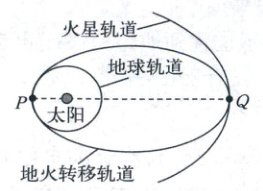
1. (2025 江西联考)“天问一号”探测器从地球发射后，经地火转移椭圆轨道再进入火星轨道(圆轨道)。探测器在椭圆轨道的近日点 $ P $ 和远日点 $ Q $ 的速度大小分别为 $ v_1 $、$ v_2 $，探测器从 $ P $ 运动到 $ Q $ 的时间为 $ t $。仅考虑太阳对探测器的引力，火星的公转周期为(C)


A.$ 2t\sqrt{\dfrac{2v_1^3}{(v_1 + v_2)^3}} $
B.$ 3t\sqrt{\dfrac{2v_1^2}{(v_1 + v_2)^3}} $
C.$ 4t\sqrt{\dfrac{2v_1^3}{(v_1 + v_2)^3}} $
D.$ 5t\sqrt{\dfrac{2v_1^3}{(v_1 + v_2)^3}} $

答案： C 解析:设P、Q两点到太阳中心的距离分别为$r_1$、$r_2$，根据开普勒第二定律可得$r_1v_1 = r_2v_2$，所以$r_2 = \frac{v_1}{v_2} · r_1$，根据开普勒第三定律变式有$\frac{T^2}{(2t)^2} = \frac{r_2^3}{(\frac{r_1 + r_2}{2})^3}$，解得火星的公转周期$T = 4t\sqrt{\frac{2v_1^3}{(v_1 + v_2)^3}}$，故C正确。

2. (2025 江西临川一中质量监测)卫星在不同轨道绕地球做圆周运动，卫星速率平方的倒数 $ \dfrac{1}{v^2} $ 与轨道高度 $ h $ 的关系图像如图所示，已知图线的纵截距为 $ b $，斜率为 $ k $，引力常量为 $ G $，则(C)


A.地球的半径为 $ \dfrac{b^2}{k} $
B.地球表面附近的重力加速度为 $ kb^2 $
C.地球的质量为 $ \dfrac{1}{kG} $
D.地球的平均密度为 $ \dfrac{3b^3}{4\pi Gk^4} $

答案： C 解析:设地球半径为R，卫星的轨道高度为h，由万有引力提供向心力有$\frac{GMm}{(R + h)^2} = m\frac{v^2}{R + h}$，又$M = \rho · \frac{4}{3}\pi R^3$，联立得$\frac{1}{v^2} = \frac{3}{4\pi GR^3\rho}h + \frac{3}{4\pi GR^2\rho}$，所以$k = \frac{3}{4\pi GR^3\rho}$，$b = \frac{3}{4\pi GR^2\rho}$，求得地球的半径$R = \frac{b}{k}$，故A错误；对在地球表面附近绕地球做匀速圆周运动的物体，有$g = \frac{v_0^2}{R}$，结合题图可得$\frac{1}{v_0^2} = b$，求得地球表面附近的重力加速度$g = \frac{k}{b^2}$，故B错误；地球表面的物体所受重力等于万有引力，即$mg = G\frac{Mm}{R^2}$，可得$M = \frac{gR^2}{G} = \frac{1}{kG}$，故C正确；由上述分析可得$\rho = \frac{3k^2}{4\pi Gb^3}$，故D错误。

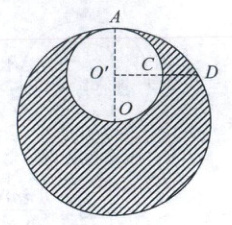
3. (多选，2024 安徽黄山期末)如图所示，均匀球体的球心为 $ O $，半径为 $ R $，质量为 $ M $，现被挖去一个球形空腔，此空腔与原球面内切于 $ A $ 点，$ AO $ 为球形空腔的一条直径，球形空腔的球心为 $ O' $，$ O'C $ 为与 $ AO $ 垂直的半径，$ D $ 与 $ O'C $ 共线且在球体表面，现将一质量为 $ m $ 的小球(可视为质点)放在球体的球面上，引力常量为 $ G $，下列关于该球剩余部分对小球的万有引力判断正确的是(AD)


A.小球在 $ D $ 处所受的万有引力大于在 $ A $ 处所受的万有引力
B.若小球放在 $ A $ 处，所受的万有引力大小为 $ \dfrac{7GMm}{8R^2} $
C.小球放在 $ A $ 处所受的万有引力最大
D.小球在 $ D $ 处所受的万有引力方向与 $ O'D $ 的夹角大于 $ 30^{\circ} $

答案： AD 解析:根据万有引力定律公式$F = \frac{GMm}{r^2}$，可知未挖去球形空腔时，整个球体对A、D两点的小球的万有引力相等，挖去空腔的球形质量对A点的引力较大，根据割补的思想可知，小球在D处所受的万有引力大于在A处所受的万有引力，故A正确，C错误；根据万有引力定律有$F_{整} = \frac{GMm}{R^2}$，$F_{空} = \frac{GM'm}{(\frac{R}{2})^2}$，由于密度相等，则$M' = \frac{1}{8}M$，解得小球放在A处，所受的万有引力大小为$F' = F_{整} - F_{空} = \frac{GMm}{2R^2}$，故B错误；根据半径关系可知，未挖去球形空腔时，小球在D处所受的万有引力方向与$O'D$的夹角为$30°$，挖去空腔后，夹角大于$30°$，故D正确。

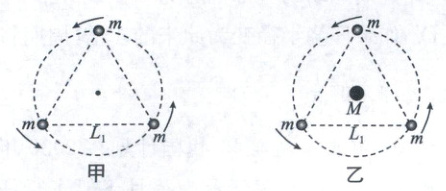
4. (2024 中学生标准学术能力诊断性测试)如图所示，甲、乙分别为常见的三星系统模型和四星系统模型。甲图中三颗质量均为 $ m $ 的行星都绕边长为 $ L_1 $ 的等边三角形的中心做匀速圆周运动，周期为 $ T_1 $；乙图中三颗质量均为 $ m $ 的行星都绕静止于边长为 $ L_2 $ 的等边三角形中心的中央星做匀速圆周运动，周期为 $ T_2 $，不考虑其他星系的影响。已知四星系统内中央星的质量 $ M = \sqrt{3}m $，$ L_2 = 2L_1 $，则两个系统的周期之比为(B)


A.$ T_1 : T_2 = 1 : 1 $
B.$ T_1 : T_2 = 1 : \sqrt{2} $
C.$ T_1 : T_2 = 1 : \sqrt{3} $
D.$ T_1 : T_2 = 1 : 2 $

答案： B 解析:甲图中，任一颗行星轨道半径$r_1 = L_1\sin60° × \frac{2}{3} = \frac{\sqrt{3}}{3}L_1$，任意两星间的万有引力，$F = G\frac{m^2}{L_1^2}$，任一颗行星$F_{合} = 2F\cos30° = \sqrt{3}F$，由牛顿第二定律可得$F_{合} = m(\frac{2\pi}{T_1})^2r_1$，解得$T_1 = 2\pi\sqrt{\frac{L_1^3}{3Gm}}$。乙图中，任一颗行星轨道半径$r_2 = L_2\sin60° × \frac{2}{3} = \frac{\sqrt{3}}{3}L_2$，每颗星受到的万有引力的合力为$F'_{合} = \frac{G\sqrt{3}m^2}{(\frac{\sqrt{3}}{3}L_2)^2} + \frac{2Gm^2}{L_2^2}\cos30°$，又$M = \sqrt{3}m$，得$F'_{合} = \frac{4\sqrt{3}Gm^2}{L_2^2}$，由万有引力提供向心力得$F'_{合} = m(\frac{2\pi}{T_2})^2r_2$，解得$T_2 = 2\pi\sqrt{\frac{L_2^3}{12Gm}}$，又$L_2 = 2L_1$，联立解得$T_1:T_2 = 1:\sqrt{2}$，故B正确。

5. (2025 山东济南模拟)如图所示为地球的赤道平面图，地球以图示的方向自西向东自转。设想在赤道上，质量为 $ m $ 的物体以相对于地面的速度 $ v $ 分别自西向东和自东向西高速运动时，两种情况下物体对水平地面压力大小之差的绝对值为 $ \Delta N $。地球可视为质量均匀球体，则地球的自转周期为(A)


A.$ \dfrac{8\pi mv}{\Delta N} $
B.$ \dfrac{4\pi mv}{\Delta N} $
C.$ \dfrac{8\pi^2 mv}{\Delta N} $
D.$ \dfrac{4\pi^2 mv}{\Delta N} $

答案： A 解析:设地球自转角速度为$\omega$，地球半径为R，地球对质量为m的物体的吸引力为$F_{引}$，当物体以相对于地面的速度v自西向东转动时有$m\frac{(v + \omega R)^2}{R} = F_{引}-F_{N1}$，物体以相对于地面的速度v自东向西转动时有$m\frac{(v - \omega R)^2}{R} = F_{引} - F_{N2}$，由题意可知$\Delta N = m\frac{(v + \omega R)^2}{R} - m\frac{(v - \omega R)^2}{R}$，整理可得$\omega = \frac{\Delta N}{4mv}$，又$\omega = \frac{2\pi}{T}$，故地球自转周期$T = \frac{8\pi mv}{\Delta N}$，故A正确。