2025年小题狂做高中物理必修第二册人教版巅峰版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年小题狂做高中物理必修第二册人教版巅峰版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第5页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
10. (2024 山西大同检测)一物体在如图甲所示的xOy平面上运动,其x轴方向的v_x-t图像如图乙所示,y轴方向的轨迹方程为$y= \frac{1}{2}t²-2t+3(m),$已知t=0时物体的位置坐标为(1m,3m),下列说法正确的是 (
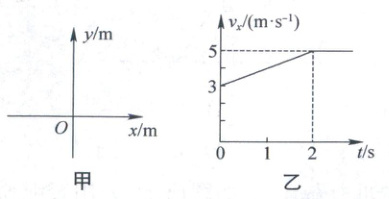
A.t=0时,物体的速度大小为5m/s
B.t=2s时,物体的位置坐标为(8m,1m)
C.前2s物体在y轴方向的加速度越来越小
D.物体在前2s做加速度大小a=√2 m/s²的曲线运动
D
)
A.t=0时,物体的速度大小为5m/s
B.t=2s时,物体的位置坐标为(8m,1m)
C.前2s物体在y轴方向的加速度越来越小
D.物体在前2s做加速度大小a=√2 m/s²的曲线运动
答案:
10. D 解析:对比匀变速直线运动的位移与时间的关系式$x = v_0t + \frac{1}{2}at^2$,与题干中的轨迹方程$y = \frac{1}{2}t^2 - 2t + 3(m)$,可知$v_{0y} = -2\ m/s$,$a_y = 1\ m/s^2$,则前$2\ s$物体在$y$轴方向的加速度恒定不变,故C错误;由题图乙可知,$t = 0$时$v_x = 3\ m/s$,所以物体的速度即合速度大小为$v = \sqrt{v_x^2 + v_{0y}^2} = \sqrt{13}\ m/s$,故A错误;在$v_x - t$图像中,图线与横轴围成的面积表示$x$轴方向的位移,则前$2\ s$物体的位移$x_x = \frac{3 + 5}{2} × 2\ m = 8\ m$,由于已知$t = 0$时物体的位置坐标为$(1\ m, 3\ m)$,则$t = 2\ s$时,$x$轴坐标为$x = 1\ m + 8\ m = 9\ m$,$y$轴坐标为$y = \frac{1}{2} × 2^2 - 2 × 2 + 3(m) = 1\ m$,此时物体的位置坐标为$(9\ m, 1\ m)$,故B错误;前$2\ s$物体在$x$轴方向的加速度为$a_x = \frac{\Delta v_x}{\Delta t} = 1\ m/s^2$,则物体在前$2\ s$的合加速度大小为$a = \sqrt{a_x^2 + a_y^2} = \sqrt{2}\ m/s^2$,由几何关系可知,合初速度与合加速度不共线,故物体在前$2\ s$做加速度大小$a = \sqrt{2}\ m/s^2$的曲线运动,故D正确.
11. (2025 哈师大附中、东北师大附中联考)法国科学家皮埃尔·德·费马在1662年提出光线传播的路径是所需时间最少的路径,即费马原理,光的折射即遵从这一原理.实际生活中的一些现象也可类比折射定律来理解.如图所示,地面上陶陶在距笔直的河岸10m处的A点,发现落水的琪琪位于水面上距河岸50m处的B点.陶陶在地面上奔跑的速度大小为$v_1=5m/s,$在水中游泳的速度大小为$v_2,$奔跑、游泳均视为匀速直线运动.可知此次营救中,陶陶在陆地的速度与河岸夹角30°,在水中的速度与河岸夹角60°将最省时.由题中信息和所学物理知识可知 (
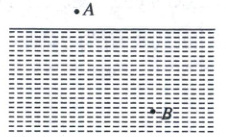
A.陶陶在水中游泳的速度大小为$v_2= \frac{5√3}{3} m/s$
B.陶陶在水中游泳的速度大小为$v_2=2.5m/s$
C.陶陶到达琪琪处的最短时间为12s
D.陶陶到达琪琪处的最短时间约为16s
A
)
A.陶陶在水中游泳的速度大小为$v_2= \frac{5√3}{3} m/s$
B.陶陶在水中游泳的速度大小为$v_2=2.5m/s$
C.陶陶到达琪琪处的最短时间为12s
D.陶陶到达琪琪处的最短时间约为16s
答案:
11. A 解析:已知陶陶在陆地的速度为$v_1$,与河岸夹角为$\alpha = 30°$;在水中的速度为$v_2$,与河岸夹角为$\beta = 60°$,将陶陶的运动分解为沿河岸方向和垂直河岸方向,在陆地时,垂直河岸方向分速度$v_{1y} = v_1 \sin\alpha$,在水中时,垂直河岸方向分速度$v_{2y} = v_2 \sin\beta$,因为要保证最省时,也就是整个运动过程中垂直河岸方向要以最大的有效速度去通过相应的距离,所以各段垂直河岸方向的分速度应该相等,即$v_{1y} \sin\alpha = v_{2y} \sin\beta$,解得$v_2 = \frac{5\sqrt{3}}{3}\ m/s$,A正确,B错误. 首先计算垂直河岸方向需要通过的总距离,在陆地上距离河岸$10\ m$,在水中距离河岸$50\ m$,所以垂直河岸方向总的距离$d = (10 + 50)m = 60\ m$,而垂直河岸方向的分速度$v_y = v_1 \sin\alpha = 2.5\ m/s$(前面已分析各段垂直河岸方向分速度相等),则最短时间$t = \frac{d}{v_y} = 24\ s$,C、D错误.
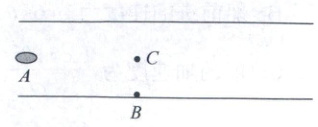
12. (福建泉州期中)如图所示,某条河流的宽度d=100m,水流速度$v_1=4m/s,$河中央处有一漂流物A(可视为质点)顺流而下.值班员在观察点B发现漂流物时,距漂流物A的平行河岸距离L=100m,当即驾驶快艇去拦截漂流物,刚好在观察点正前方的C处拦截到漂流物,BC连线垂直河岸,此过程中快艇相对于水的速度恒定.求:
(1) 快艇速度的大小和方向.
(2) 若水流速度加倍后仅将快艇的行驶速度大小加倍,则是否可以完成任务? (需说明理由)
(1) 快艇速度的大小和方向.
(2) 若水流速度加倍后仅将快艇的行驶速度大小加倍,则是否可以完成任务? (需说明理由)
(1)要刚好在C点完成拦截,漂流物到达C点的时间$t = \frac{L}{v_1}$,解得$t = 25\ s$,快艇的实际行驶速度方向必须是沿BC方向,则有$\frac{1}{2}d = \frac{1}{2}vt$,解得$v = 2\ m/s$,由几何关系可知$v_{艇}^2 = v_1^2 + v^2$,解得$v_{艇} = 2\sqrt{5}\ m/s$,设快艇的速度方向与河岸成$\alpha$角,有$\tan\alpha = \frac{v}{v_1}$,解得$\tan\alpha = \frac{1}{2}$。
(2)当水流速度加倍后漂流物到达C点的时间$t' = \frac{L}{2v_1} = 12.5\ s$,快艇的实际行驶速度方向必须是沿BC方向,则有$\frac{1}{2}d = \frac{1}{2}v't$,解得$v' = 4\ m/s$,由几何关系可知$(v_{艇}')^2 = (v_1')^2 + (v')^2$,其中$v_1' = 2v_1$,解得$v_{艇}' = 4\sqrt{5}\ m/s$,设快艇的速度方向与河岸成$\alpha'$角,有$\tan\alpha' = \frac{v'}{v_1} = \frac{1}{2} = \tan\alpha$,则可以完成任务.
(2)当水流速度加倍后漂流物到达C点的时间$t' = \frac{L}{2v_1} = 12.5\ s$,快艇的实际行驶速度方向必须是沿BC方向,则有$\frac{1}{2}d = \frac{1}{2}v't$,解得$v' = 4\ m/s$,由几何关系可知$(v_{艇}')^2 = (v_1')^2 + (v')^2$,其中$v_1' = 2v_1$,解得$v_{艇}' = 4\sqrt{5}\ m/s$,设快艇的速度方向与河岸成$\alpha'$角,有$\tan\alpha' = \frac{v'}{v_1} = \frac{1}{2} = \tan\alpha$,则可以完成任务.

答案:
12. (1)要刚好在C点完成拦截,漂流物到达C点的时间$t = \frac{L}{v_1}$,解得$t = 25\ s$,快艇的实际行驶速度方向必须是沿BC方向,则有$\frac{1}{2}d = \frac{1}{2}vt$,解得$v = 2\ m/s$,由几何关系可知$v_{艇}^2 = v_1^2 + v^2$,解得$v_{艇} = 2\sqrt{5}\ m/s$,设快艇的速度方向与河岸成$\alpha$角,有$\tan\alpha = \frac{v}{v_1}$,解得$\tan\alpha = \frac{1}{2}$。
(2)当水流速度加倍后漂流物到达C点的时间$t' = \frac{L}{2v_1} = 12.5\ s$,快艇的实际行驶速度方向必须是沿BC方向,则有$\frac{1}{2}d = \frac{1}{2}v't$,解得$v' = 4\ m/s$,由几何关系可知$(v_{艇}')^2 = (v_1')^2 + (v')^2$,其中$v_1' = 2v_1$,解得$v_{艇}' = 4\sqrt{5}\ m/s$,设快艇的速度方向与河岸成$\alpha'$角,有$\tan\alpha' = \frac{v'}{v_1} = \frac{1}{2} = \tan\alpha$,则可以完成任务.
(2)当水流速度加倍后漂流物到达C点的时间$t' = \frac{L}{2v_1} = 12.5\ s$,快艇的实际行驶速度方向必须是沿BC方向,则有$\frac{1}{2}d = \frac{1}{2}v't$,解得$v' = 4\ m/s$,由几何关系可知$(v_{艇}')^2 = (v_1')^2 + (v')^2$,其中$v_1' = 2v_1$,解得$v_{艇}' = 4\sqrt{5}\ m/s$,设快艇的速度方向与河岸成$\alpha'$角,有$\tan\alpha' = \frac{v'}{v_1} = \frac{1}{2} = \tan\alpha$,则可以完成任务.
查看更多完整答案,请扫码查看


