2025年小题狂做高中物理必修第二册人教版巅峰版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年小题狂做高中物理必修第二册人教版巅峰版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第60页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
5. (多选,2024 浙江杭州期中)地月系统可被认为是月球绕地球做匀速圆周运动,如图甲所示,月球绕地球运动的周期为 $ T_1 $;也可认为地月系统是一个双星系统,如图乙所示,在相互之间的万有引力作用下,绕连线上的 $ O $ 点做匀速圆周运动,月球绕 $ O $ 点运动的周期为 $ T_2 $. 若地球、月球的质量分别为 $ M $、$ m $,两球心相距为 $ r $,引力常量为 $ G $,下列说法正确的是(
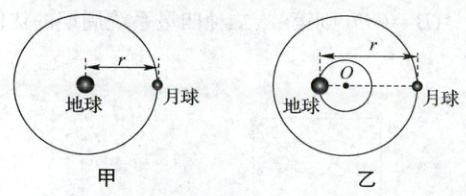
A.图甲中月球绕地球运动的周期 $ T_1 $ 大于图乙中月球绕 $ O $ 点运动的周期 $ T_2 $
B.图甲中,地球的密度为 $ \frac{3\pi}{GT_1^2} $
C.地月双星轨道中 $ O $ 点到地心的距离为 $ \frac{M}{M + m}r $
D.图甲中,若把部分月壤运回到地球,最终月球绕地球做圆周运动的轨道半径将变小
AD
)
A.图甲中月球绕地球运动的周期 $ T_1 $ 大于图乙中月球绕 $ O $ 点运动的周期 $ T_2 $
B.图甲中,地球的密度为 $ \frac{3\pi}{GT_1^2} $
C.地月双星轨道中 $ O $ 点到地心的距离为 $ \frac{M}{M + m}r $
D.图甲中,若把部分月壤运回到地球,最终月球绕地球做圆周运动的轨道半径将变小
答案:
5.AD解析:由万有引力提供向心力有$G\frac{Mm}{r^{2}} = m\frac{4\pi^{2}}{T^{2}}r$,解得题图甲中月球绕地球运动的周期为$T_{1} = 2\pi\sqrt{\frac{r^{3}}{GM}}$,若地月系统是一个双星系统,设地月双星轨道中$O$点到地心的距离为$r_{1}$,到月球球心的距离为$r_{2}$,则$G\frac{Mm}{r^{2}} = M\frac{4\pi^{2}}{T_{2}^{2}}r_{1}$,$G\frac{Mm}{r^{2}} = m\frac{4\pi^{2}}{T_{2}^{2}}r_{2}$,$r = r_{1} + r_{2}$,可得$r_{1} = \frac{m}{M + m}r$,$T_{2} = 2\pi\sqrt{\frac{r^{3}}{G(M + m)}} < T_{1}$,即题图甲中月球绕地球运动的周期大于题图乙中月球绕$O$点运动的周期,A正确,C错误;设地球的半径为$R$,故地球的密度为$\rho = \frac{M}{V} = \frac{\frac{4\pi^{2}r^{3}}{GT_{1}^{2}r_{1}^{3}}}{ \frac{4}{3}\pi R^{3}} = \frac{3\pi r^{3}}{GT_{1}^{2}R^{3}}$,B错误;题图甲中,若把部分月壤运回到地球,设部分月壤的质量为$\Delta m$,则$(m - \Delta m)\frac{4\pi^{2}}{T_{1}^{2}}r < G\frac{(M + \Delta m)(m - \Delta m)}{r^{2}}$,即此时月球做圆周运动所需的向心力小于月球与地球间的万有引力,月球做近心运动,月球绕地球做圆周运动的轨道半径将变小,D正确。
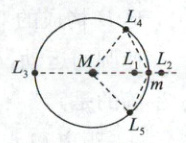
6. 拉格朗日点指在两个大天体引力作用下,能使小物体稳定的点(小物体质量相对两大天体可忽略不计). 这些点的存在由法国数学家拉格朗日于 1772 年推导证明的,1906 年首次发现运动于木星轨道上的小行星(见脱罗央群小行星)在木星和太阳的作用下处于拉格朗日点上. 在每个由两大天体构成的系统中,按推论有 5 个拉格朗日点,其中连线上有三个拉格朗日点,分别是 $ L_1 $、$ L_2 $、$ L_3 $,如图所示. 我国发射的“鹊桥”卫星就在地月系统平衡点 $ L_2 $ 点做周期运动,通过定期轨控保持轨道的稳定性,可实现对着陆器和巡视器的中继通信覆盖,首次实现地月 $ L_2 $ 点周期轨道的长期稳定运行. 设某两个天体系统的中心天体质量为 $ M $,环绕天体质量为 $ m $,两天体间距离为 $ L $,引力常量为 $ G $,$ L_1 $ 点到中心天体的距离为 $ R_1 $,$ L_2 $ 点到中心天体的距离为 $ R_2 $. 求:
(1) 处于 $ L_1 $ 点小物体的向心加速度;
(2) 处于 $ L_2 $ 点小物体运行的线速度;
(3) 为了进一步的通信覆盖,发射两颗质量均为 $ m_0 $ 的卫星,分别处于 $ L_1 $、$ L_2 $ 点,$ L_1 $、$ L_2 $ 到环绕天体的距离近似相等(远小于 $ L $),两卫星与环绕天体同步绕中心天体做圆周运动,忽略卫星间的引力,求中心天体对环绕天体的引力与它对两卫星的引力之和的比值?
(1) 处于 $ L_1 $ 点小物体的向心加速度;
(2) 处于 $ L_2 $ 点小物体运行的线速度;
(3) 为了进一步的通信覆盖,发射两颗质量均为 $ m_0 $ 的卫星,分别处于 $ L_1 $、$ L_2 $ 点,$ L_1 $、$ L_2 $ 到环绕天体的距离近似相等(远小于 $ L $),两卫星与环绕天体同步绕中心天体做圆周运动,忽略卫星间的引力,求中心天体对环绕天体的引力与它对两卫星的引力之和的比值?

答案:
6.
(1)设处于$L_{1}$点的小物体质量为$m_{0}$,则小物体所受向心力由两天体的万有引力的合力来提供,可得$G\frac{Mm_{0}}{R_{1}^{2}} - G\frac{mm_{0}}{(L - R_{1})^{2}} = m_{0}a_{向}$,解得$a_{向} = \frac{GM}{R_{1}^{2}} - \frac{Gm}{(L - R_{1})^{2}}$。
(2)设处于$L_{2}$点的小物体质量为$m_{0}$,则小物体所受向心力由两天体的万有引力的合力来提供,可得$G\frac{Mm_{0}}{R_{2}^{2}} + G\frac{mm_{0}}{(R_{2} - L)^{2}} = m_{0}\frac{v^{2}}{R_{2}}$,解得$v = \sqrt{G\frac{M}{R_{2}} + G\frac{mR_{2}}{(R_{2} - L)^{2}}}$。
(3)中心天体对环绕天体的引力为$F_{1} = G\frac{Mm}{L^{2}}$,中心天体对两卫星的引力之和为$F_{2} = G\frac{Mm_{0}}{R_{1}^{2}} + G\frac{Mm_{0}}{R_{2}^{2}} = GMm_{0}(\frac{1}{R_{1}^{2}} + \frac{1}{R_{2}^{2}})$,设处于$L_{2}$点的小物体与环绕天体相距$x$,由于$x$远小于$L$,所以有$\frac{1}{R_{1}^{2}} + \frac{1}{R_{2}^{2}} = \frac{1}{(L - x)^{2}} + \frac{1}{(L + x)^{2}} \approx \frac{2}{L^{2}}$,则中心天体对环绕天体的引力与它对两卫星的引力之和的比值为$\frac{F_{1}}{F_{2}} = \frac{m}{2m_{0}}$。
(1)设处于$L_{1}$点的小物体质量为$m_{0}$,则小物体所受向心力由两天体的万有引力的合力来提供,可得$G\frac{Mm_{0}}{R_{1}^{2}} - G\frac{mm_{0}}{(L - R_{1})^{2}} = m_{0}a_{向}$,解得$a_{向} = \frac{GM}{R_{1}^{2}} - \frac{Gm}{(L - R_{1})^{2}}$。
(2)设处于$L_{2}$点的小物体质量为$m_{0}$,则小物体所受向心力由两天体的万有引力的合力来提供,可得$G\frac{Mm_{0}}{R_{2}^{2}} + G\frac{mm_{0}}{(R_{2} - L)^{2}} = m_{0}\frac{v^{2}}{R_{2}}$,解得$v = \sqrt{G\frac{M}{R_{2}} + G\frac{mR_{2}}{(R_{2} - L)^{2}}}$。
(3)中心天体对环绕天体的引力为$F_{1} = G\frac{Mm}{L^{2}}$,中心天体对两卫星的引力之和为$F_{2} = G\frac{Mm_{0}}{R_{1}^{2}} + G\frac{Mm_{0}}{R_{2}^{2}} = GMm_{0}(\frac{1}{R_{1}^{2}} + \frac{1}{R_{2}^{2}})$,设处于$L_{2}$点的小物体与环绕天体相距$x$,由于$x$远小于$L$,所以有$\frac{1}{R_{1}^{2}} + \frac{1}{R_{2}^{2}} = \frac{1}{(L - x)^{2}} + \frac{1}{(L + x)^{2}} \approx \frac{2}{L^{2}}$,则中心天体对环绕天体的引力与它对两卫星的引力之和的比值为$\frac{F_{1}}{F_{2}} = \frac{m}{2m_{0}}$。
7. (2025 重庆八中开学考)中科院国家天文台的科学家观测到三颗星 $ A $、$ B $、$ C $ 保持相对静止,相互之间的距离均为 $ l $,且一起绕着某点做周期为 $ T $ 的匀速圆周运动. 已知 $ m_A = m $,$ m_B = m_C = (\sqrt{3} + 1)m $,不计其他星体对它们的影响. 关于这个三星系统,则(

A.三颗星 $ A $、$ B $、$ C $ 的轨道半径之比为 $ 1 : \sqrt{2} : \sqrt{2} $
B.三颗星 $ A $、$ B $、$ C $ 的角速度大小之比为 $ \sqrt{2} : 1 : 1 $
C.若距离 $ l $ 均不变,$ A $、$ B $、$ C $ 的质量均变为原来的 3 倍,则周期变为 $ \frac{\sqrt{3}}{3}T $
D.若 $ A $、$ B $、$ C $ 的质量不变,距离均变为 $ 2l $,则周期变为 $ \sqrt{2}T $
C
)
A.三颗星 $ A $、$ B $、$ C $ 的轨道半径之比为 $ 1 : \sqrt{2} : \sqrt{2} $
B.三颗星 $ A $、$ B $、$ C $ 的角速度大小之比为 $ \sqrt{2} : 1 : 1 $
C.若距离 $ l $ 均不变,$ A $、$ B $、$ C $ 的质量均变为原来的 3 倍,则周期变为 $ \frac{\sqrt{3}}{3}T $
D.若 $ A $、$ B $、$ C $ 的质量不变,距离均变为 $ 2l $,则周期变为 $ \sqrt{2}T $
答案:
7.C解析:由于三颗星保持相对静止,一起绕着某点做圆周运动,三星角速度与周期相等,根据对称性,$B$、$C$轨道半径相等,作出三星运动轨迹,如图所示,对$A$星体有$2G\frac{(\sqrt{3} + 1)m^{2}}{l^{2}}\cos 30^{\circ} = m\omega^{2}R_{A}$,对$B$、$C$星体,两星体各自所受引力的合力大小相等,设为$F$,根据余弦定理有$F^{2} = [G\frac{(\sqrt{3} + 1)^{2}m^{2}}{l^{2}}]^{2} + [G\frac{(\sqrt{3} + 1)m^{2}}{l^{2}}]^{2} - 2G^{2}\frac{(\sqrt{3} + 1)^{2}m^{2}}{l^{2}} · \frac{(\sqrt{3} + 1)m^{2}}{l^{2}}\cos 120^{\circ}$,对$B$、$C$星体,两星体各自做圆周运动,$B$、$C$轨道半径相等,令为$R_{B} = R_{C} = R_{0}$,则有$F = (\sqrt{3} + 1)m\omega^{2}R_{0}$,解得$\frac{R_{A}}{R_{0}} = \sqrt{2}$,可知三颗星$A$、$B$、$C$的半径大小之比为$\sqrt{2}:1:1$,故A错误;三颗星$A$、$B$、$C$的角速度相等,故三颗星$A$、$B$、$C$的角速度大小之比为$1:1:1$,故B错误;距离$l$均不变,对$A$星体有$2G\frac{(\sqrt{3} + 1)m^{2}}{l^{2}}\cos 30^{\circ} = m\frac{4\pi^{2}}{T_{1}^{2}}R_{A}$,若$A$、$B$、$C$的质量均变为原来的$3$倍,根据对称性可知,三星圆周运动的圆心不变,即轨道半径不变,则有$2G\frac{9 × (\sqrt{3} + 1)m^{2}}{l^{2}}\cos 30^{\circ} = 3m\frac{4\pi^{2}}{T_{1}^{2}}R_{A}$,解得$T_{1} = \frac{\sqrt{3}T}{3}$,故C正确;若$A$、$B$、$C$的质量不变,距离均变为$2l$,根据对称性可知,三星圆周运动的圆心不变,即轨道半径均变为先前的$2$倍,则对$A$星有$2G\frac{(\sqrt{3} + 1)m^{2}}{(2l)^{2}}\cos 30^{\circ} = m\frac{4\pi^{2}}{T_{2}^{2}} · 2R_{A}$,解得$T_{2} = 2\sqrt{2}T$,即若$A$、$B$、$C$的质量不变,距离均变为$2l$,则周期变为$2\sqrt{2}T$,故D错误。

7.C解析:由于三颗星保持相对静止,一起绕着某点做圆周运动,三星角速度与周期相等,根据对称性,$B$、$C$轨道半径相等,作出三星运动轨迹,如图所示,对$A$星体有$2G\frac{(\sqrt{3} + 1)m^{2}}{l^{2}}\cos 30^{\circ} = m\omega^{2}R_{A}$,对$B$、$C$星体,两星体各自所受引力的合力大小相等,设为$F$,根据余弦定理有$F^{2} = [G\frac{(\sqrt{3} + 1)^{2}m^{2}}{l^{2}}]^{2} + [G\frac{(\sqrt{3} + 1)m^{2}}{l^{2}}]^{2} - 2G^{2}\frac{(\sqrt{3} + 1)^{2}m^{2}}{l^{2}} · \frac{(\sqrt{3} + 1)m^{2}}{l^{2}}\cos 120^{\circ}$,对$B$、$C$星体,两星体各自做圆周运动,$B$、$C$轨道半径相等,令为$R_{B} = R_{C} = R_{0}$,则有$F = (\sqrt{3} + 1)m\omega^{2}R_{0}$,解得$\frac{R_{A}}{R_{0}} = \sqrt{2}$,可知三颗星$A$、$B$、$C$的半径大小之比为$\sqrt{2}:1:1$,故A错误;三颗星$A$、$B$、$C$的角速度相等,故三颗星$A$、$B$、$C$的角速度大小之比为$1:1:1$,故B错误;距离$l$均不变,对$A$星体有$2G\frac{(\sqrt{3} + 1)m^{2}}{l^{2}}\cos 30^{\circ} = m\frac{4\pi^{2}}{T_{1}^{2}}R_{A}$,若$A$、$B$、$C$的质量均变为原来的$3$倍,根据对称性可知,三星圆周运动的圆心不变,即轨道半径不变,则有$2G\frac{9 × (\sqrt{3} + 1)m^{2}}{l^{2}}\cos 30^{\circ} = 3m\frac{4\pi^{2}}{T_{1}^{2}}R_{A}$,解得$T_{1} = \frac{\sqrt{3}T}{3}$,故C正确;若$A$、$B$、$C$的质量不变,距离均变为$2l$,根据对称性可知,三星圆周运动的圆心不变,即轨道半径均变为先前的$2$倍,则对$A$星有$2G\frac{(\sqrt{3} + 1)m^{2}}{(2l)^{2}}\cos 30^{\circ} = m\frac{4\pi^{2}}{T_{2}^{2}} · 2R_{A}$,解得$T_{2} = 2\sqrt{2}T$,即若$A$、$B$、$C$的质量不变,距离均变为$2l$,则周期变为$2\sqrt{2}T$,故D错误。

查看更多完整答案,请扫码查看


