2025年小题狂做高中物理必修第二册人教版巅峰版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年小题狂做高中物理必修第二册人教版巅峰版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第23页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
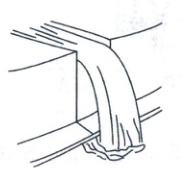
1. (2024 四川成都月考)某生态公园的人造瀑布景观如图所示,水流从高处水平流出槽道,恰好落入步道边的游泳池中。现制作一个为实际尺寸$\frac{1}{16}$的模型展示效果,模型中槽道里的水流速度应为实际的(
A.$\frac{1}{2}$
B.$\frac{1}{4}$
C.$\frac{1}{10}$
D.$\frac{1}{16}$
B
)
A.$\frac{1}{2}$
B.$\frac{1}{4}$
C.$\frac{1}{10}$
D.$\frac{1}{16}$
答案:
1.B 解析:水流从高处水平流出槽道后做平抛运动,现制作一个为实际尺寸$\frac{1}{16}$的模型,可知模型中竖直高度和水平位移应都为原来的$\frac{1}{16}$,根据平抛运动规律,竖直方向上有$h = \frac{1}{2} g t^{2}$,$h_{模} = \frac{1}{16} h_{实}$,可知模型中的时间$t_{模} = \frac{1}{4} t_{实}$,水平方向上有$x = v_{0} t$,$x_{模} = \frac{1}{16} x_{实}$,可知$v_{0模} = \frac{1}{4} v_{0实}$,故B正确.
易错提醒 本题容易错选D,主要原因是错误地认为水平速度只与水平距离有关,根据模型水平尺寸为实际尺寸的$\frac{1}{16}$,得出模型中槽道里的水流速度为实际的$\frac{1}{16}$.
易错提醒 本题容易错选D,主要原因是错误地认为水平速度只与水平距离有关,根据模型水平尺寸为实际尺寸的$\frac{1}{16}$,得出模型中槽道里的水流速度为实际的$\frac{1}{16}$.
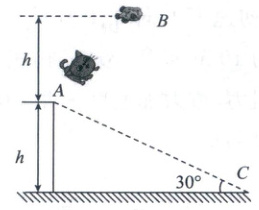
2. (2025 浙江绍兴期末)猫咪在离地$h$的桌上$A$向上跃起刚够到$B$处离桌面高$h$的玩具,最后落地点为$C$,$AC$与水平方向的夹角为$30^{\circ}$,猫咪可视为质点。下列说法错误的是(
A.$A$到$B$的时间与$B$到$C$的时间之比为$1:\sqrt{2}$
B.猫咪水平方向的速度为$\frac{(2-\sqrt{2})\sqrt{3gh}}{2}$
C.猫咪从$B$到$C$的水平位移为$(\sqrt{6}-\sqrt{2})h$
D.猫咪在空中的时间为$\sqrt{\frac{h}{g}}(\sqrt{2}+2)$
C
)
A.$A$到$B$的时间与$B$到$C$的时间之比为$1:\sqrt{2}$
B.猫咪水平方向的速度为$\frac{(2-\sqrt{2})\sqrt{3gh}}{2}$
C.猫咪从$B$到$C$的水平位移为$(\sqrt{6}-\sqrt{2})h$
D.猫咪在空中的时间为$\sqrt{\frac{h}{g}}(\sqrt{2}+2)$
答案:
2.C 解析:猫咪向上运动时有$h = \frac{1}{2} g t_{1}^{2}$,向下运动时有$2h = \frac{1}{2} g t_{2}^{2}$,解得$\frac{t_{1}}{t_{2}} = \frac{1}{\sqrt{2}}$,在空中的时间为$t = t_{1} + t_{2} = \sqrt{\frac{h}{g}} (\sqrt{2} + 2)$,A、D正确;水平方向有$\frac{h'}{\tan 30^{\circ}} = v_{x} (t_{1} + t_{2})$,解得$v_{x} = \frac{(2 - \sqrt{2}) \sqrt{3gh}}{2}$,B正确;猫咪从B到C的水平位移为$x_{BC} = v_{x} t_{2} = (2 \sqrt{3} - \sqrt{6}) h$,C错误.
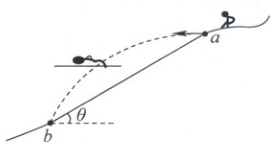
3. (多选,天津期中)滑雪是一项勇敢者的运动,运动员穿着专用的滑雪板,从弧形的雪坡上$a$点沿水平方向飞出后,又落回到足够长的倾斜雪坡上的$b$点。如图所示,倾斜的雪坡(视为斜面)倾角为$\theta$,运动员以水平速度$v_0$飞出,且飞出后在空中的姿势保持不变,不计空气阻力,运动员从飞出到落到斜面上所用时间为$t$,运动员刚落到斜面上时速度方向与水平面的夹角为$\alpha$,重力加速度为$g$,下列说法正确的是(
A.运动员飞出时的水平速度$v_0$越小,$\alpha$越小
B.运动员刚落到斜面上时速度方向与水平面夹角的正切值是斜面倾角正切值的两倍,即$\tan\alpha = 2\tan\theta$
C.运动员从飞出到离斜面最远所用时间为$\frac{t}{2}$
D.运动员在空中离斜面的最远距离可以表示为$\frac{v_0^2\tan\theta}{2g}$
BC
)
A.运动员飞出时的水平速度$v_0$越小,$\alpha$越小
B.运动员刚落到斜面上时速度方向与水平面夹角的正切值是斜面倾角正切值的两倍,即$\tan\alpha = 2\tan\theta$
C.运动员从飞出到离斜面最远所用时间为$\frac{t}{2}$
D.运动员在空中离斜面的最远距离可以表示为$\frac{v_0^2\tan\theta}{2g}$
答案:
3.BC 解析:运动员落到斜面上的速度与水平面的夹角为$\alpha$,根据平抛运动的推论,可知$\tan \alpha = 2 \tan \theta$,斜面倾角为$\theta$不变,所以运动员落到斜面上的速度与水平面的夹角$\alpha$也不变,A错误,B正确;根据平抛运动的规律有$\tan \theta = \frac{y}{x} = \frac{gt}{2v_{0}}$,解得运动员在空中运动的时间为$t = \frac{2v_{0} \tan \theta}{g}$,设运动员从飞出到离斜面最远所用时间为$t_{1}$,有$t_{1} = \frac{v_{0} \sin \theta}{g \cos \theta} = \frac{v_{0} \tan \theta}{g} = \frac{t}{2}$,C正确;离斜面的最远距离$h = \frac{1}{2} g \cos \theta · t_{1}^{2} = \frac{v_{0}^{2} \cos \theta · \tan^{2} \theta}{2g}$,D错误.
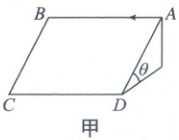
4. (多选,2024 河南濮阳名校联考)如图甲所示为一固定在水平地面、倾角为$\theta = 30^{\circ}$的斜面体,在斜面$ABCD$上固定平铺一张光滑的坐标纸,将一小球从$A$点沿$AB$以某一初速度水平推出,并用频闪照相机记录下小球在运动过程中不同时刻的位置,如图乙所示。已知坐标纸每个正方形方格的边长为$d$,照相机频闪的时间间隔为$t$,小球可视为质点,空气阻力不计。下列说法正确的是(
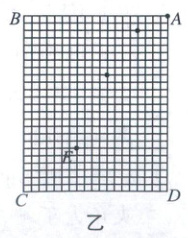
A.小球在斜面上做匀变速曲线运动
B.小球从$A$点运动到$CD$边的时间为$4.75t$
C.小球从$A$点抛出时的速度大小为$\frac{2d}{t}$
D.当地的重力加速度大小为$\frac{8d}{t^2}$
AD
)

A.小球在斜面上做匀变速曲线运动
B.小球从$A$点运动到$CD$边的时间为$4.75t$
C.小球从$A$点抛出时的速度大小为$\frac{2d}{t}$
D.当地的重力加速度大小为$\frac{8d}{t^2}$
答案:
4.AD 解析:小球在斜面上受到的合力为重力沿斜面向下的分力,恒定不变,且合力方向与初速度方向垂直,则小球在斜面上做类平抛运动,即匀变速曲线运动,A正确;小球沿初速度方向做匀速直线运动,则有$v_{A} = \frac{x}{t} = \frac{4d}{t}$,C错误;小球沿斜面向下做匀加速直线运动,则有$\Delta y = a t^{2} = 6d - 2d = 4d$,解得小球的加速度大小为$a = \frac{4d}{t^{2}}$,根据牛顿第二定律知$a = \frac{mg \sin \theta}{m} = \frac{1}{2} g$,可得当地的重力加速度大小为$g = \frac{8d}{t^{2}}$,D正确;设小球从A点运动到CD边的时间为$t'$,沿斜面向下有$24d = \frac{1}{2} a (t')^{2}$,解得$t' = \sqrt{\frac{48d}{a}} = 2 \sqrt{3} t$,B错误.
查看更多完整答案,请扫码查看


