《2025年大联考单元期末测试卷八年级数学上册沪科版》

19. 核心素养·模型观念某商店销售$A$型和$B$型两种型号的电脑，销售一台$A$型电脑可获利$120$元，销售一台$B$型电脑可获利$140$元。该商店计划一次购进两种型号的电脑共$100$台，其中$B$型电脑的进货量不超过$A$型电脑的$3$倍。设购进$A$型电脑$x$台，这$100$台电脑的销售总利润为$y$元。
（1）求$y$与$x$的函数表达式，并求出自变量$x$的取值范围。
（2）该商店购进$A$型、$B$型电脑各多少台，才能使销售利润最大？最大利润是多少？

答案： 19.解:
(1)由题意,得A型电脑的总利润为$120x$,
B型电脑的总利润为$140(100 - x)$,
　$\therefore A,B$电脑的总利润为$y = 120x + 140(100 - x)= -20x + 14000$,
　$\therefore y$与$x$的函数表达式为$y = -20x + 14000$.(3分)
　又B型电脑的进货量不超过A型电脑的3倍,
　$\therefore 100 - x \leq 3x$,解得$x \geq 25$,
　$\therefore$自变量$x$的取值范围为$25 \leq x \leq 100$,且$x$为正整数,
　$\therefore y = -20x + 14000(25 \leq x \leq 100$,且$x$为正整数).(5分)
(2)$\because y = -20x + 14000$,且$-20 ＜ 0$,
　$\therefore y$随$x$的增大而减小.(7分)
　$\because 25 \leq x \leq 100$,且$x$为正整数,
　$\therefore$当$x = 25$时,$y$有最大值为$-20×25 + 14000 = 13500$,
　$\therefore$购进A型电脑25台,B型电脑75台,销售利润最大,最大利润为13500元.(10分)

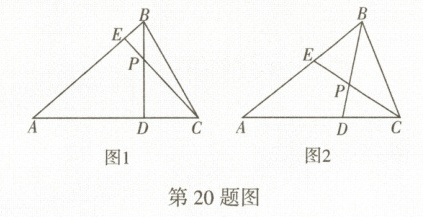
20. 在锐角三角形$ABC$中，点$E$，$D$分别为边$AB$，$AC$上的动点，连接$EC$，$BD$交于点$P$。
（1）如图$1$，当$E$，$D$运动到$CE\perp AB$，$BD\perp AC$，$\angle BPC = 130^{\circ}$，求$\angle A$的度数。
（2）如图$2$，当$E$，$D$运动到$BD$，$CE$分别平分$\angle ABC$，$\angle ACB$，写出$\angle A$与$\angle BPC$的数量关系，并证明。

答案： 20.解:
(1)由题意,得$\angle BPC = \angle DPE = 130^{\circ}$.
　在四边形$ADPE$中,$\because CE \perp AB,BD \perp AC$,
　$\therefore \angle AEP = \angle ADP = 90^{\circ}$,
　$\therefore \angle A = 360^{\circ}-\angle AEP - \angle ADP - \angle DPE = 50^{\circ}$.(5分)
(2)$\angle BPC = 90^{\circ}+\frac{1}{2}\angle A$.理由如下:(6分)
　$\because BD,CE$分别平分$\angle ABC,\angle ACB$,
　$\therefore 2\angle CBD = \angle ABC,2\angle BCE = \angle ACB$.
　$\because \angle A = 180^{\circ}-(\angle ABC + \angle ACB)$,
　$\therefore \angle A = 180^{\circ}-2(\angle DBC + \angle BCE)$,
　$\therefore \angle DBC + \angle BCE = 90^{\circ}-\frac{1}{2}\angle A$.
　在$\triangle BPC$中,$\angle BPC = 180^{\circ}-(\angle DBC + \angle BCE)$
　$= 180^{\circ}-(90^{\circ}-\frac{1}{2}\angle A)=90^{\circ}+\frac{1}{2}\angle A$.(10分)