《2025年大联考单元期末测试卷八年级数学上册沪科版》

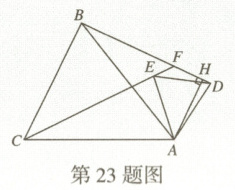
23. 核心素养·推理能力如图,在$\triangle ABC$和$\triangle ADE$中,$AB = AC$,$AD = AE$,$\angle BAC=\angle DAE$,CE的延长线交BD于点F.
(1)求证:$CE = BD$.
(2)若$\angle ACE = 30°$,$\angle BAE = 15°$,$\angle DAE=\angle AED - 6°$,求$\angle BDE$的度数.
(3)过点A作$AH\perp BD$于点H,试写出EF,FH,DH之间的数量关系,并证明.

答案：
23.解：
(1)证明：
∵∠BAC=∠DAE，
∴∠BAC+∠BAE=∠DAE+∠BAE，
即∠CAE=∠BAD.
又
∵AB=AC,AD=AE，
∴△CAE≌△BAD(SAS)，
∴CE=BD.(4分)
(2)设∠AED=x°，则∠DAE=x°-6°，
∴∠ADE=∠AED=x°.
∵∠AED+∠ADE+∠DAE=180°，
∴x+x+x-6=180，解得x=62，
∴∠ADE=∠AED=62°,∠DAE=56°.
∴∠BAD=∠DAE+∠BAE=71°.(7分)
∵△CAE≌△BAD，
∴∠ABD=∠ACE=30°，
∴∠ADB=180°-∠BAD-∠ABD=79°，
∴∠BDE=∠ADB-∠ADE=17°.(9分)
(3)EF+DH=FH.理由如下：
如图，过点A作AM⊥CF于点M，连接AF.

∵△CAE≌△BAD,AM⊥CF,AH⊥BD，
∴AM=AH(全等三角形对应边上的高相等).(11分)
又
∵AF=AF，
∴Rt△AFM≌Rt△AFH(HL)，
∴FM=FH.
又
∵AM=AH,AE=AD,∠AME=∠AHD=90°，
∴Rt△AEM≌Rt△ADH(HL)，
∴EM=DH，
∴EF+DH=EF+EM=FM=FH.(14分)