《2025年大联考单元期末测试卷八年级数学上册沪科版》

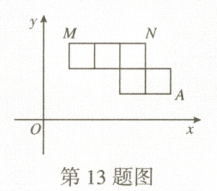
13. 如图，将5个大小相同的正方形置于平面直角坐标系中，若顶点$ M,N $的坐标分别为$ (3,9) $，$ (12,9) $，则顶点$ A $的坐标为(15,3)。

答案： 13.(15,3)

14. 新考法定义：在平面直角坐标系中，已知点$ P_1(a,b) $，$ P_2(c,b) $，$ P_3(c,d) $，这三个点中任意两点间的距离的最小值称为点$ P_1,P_2,P_3 $的“最佳间距”。例如：点$ P_1(-1,2) $，$ P_2(1,2) $，$ P_3(1,3) $的“最佳间距”是1。
(1)点$ Q_1(2,1) $，$ Q_2(5,1) $，$ Q_3(5,5) $的“最佳间距”是3。
(2)当点$ O(0,0) $，$ E(m,0) $，$ P(m,-2m+1) $的“最佳间距”为$ \frac{1}{3} $时，点$ P $的横坐标为-$\frac{1}{3}$或$\frac{1}{3}$或$\frac{2}{3}$。

答案： 14.
(1)3
(2)-$\frac{1}{3}$或$\frac{1}{3}$或$\frac{2}{3}$

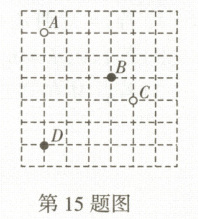
15. 新考法围棋，起源于中国，古代称为“弈”，是棋类鼻祖，距今已有4000多年的历史。如图是某围棋棋盘的局部，若棋盘是由边长均为1的小正方形组成的，棋盘上$ A,B $两颗棋子的坐标分别为$ A(-2,4) $，$ B(1,2) $。
（1）画出相应的平面直角坐标系，并写出$ C,D $两颗棋子的坐标。
（2）有一颗黑色棋子$ E $的坐标为$ (3,-1) $，请在图中画出黑色棋子$ E $。

答案：
15.解：
(1)平面直角坐标系如图所示，点C(2,1)，点D(-2,-1).(6分)

(2)如图，点E即为所求.(8分)

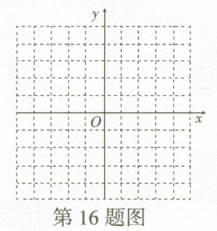
16. 如图，在平面直角坐标系中，三角形$ ABC $的三个顶点的坐标分别是$ A(-1,2) $，$ B(-3,-2) $，$ C(3,-2) $。
（1）在平面直角坐标系中画出三角形$ ABC $。
（2）求三角形$ ABC $的面积。

答案：
16.解：
(1)如图所示，三角形ABC即为所求.(4分)

(2)易知BC=6,边BC上的高为4.
$S_{三角形ABC}$=$\frac{1}{2}$×6×4=12.(8分)

17. 在平面直角坐标系中，点$ A(1,2a+3) $在第一象限。
（1）若点$ A $到$ x $轴的距离与到$ y $轴的距离相等，求$ a $的值。
（2）若点$ A $到$ x $轴的距离小于到$ y $轴的距离，求$ a $的取值范围。

答案： 17.解：
(1)因为点A到x轴的距离与到y轴的距离相等，
所以2a+3=1且2a+3＞0,解得a=-1.(4分)
(2)因为点A到x轴的距离小于到y轴的距离，且点A在第一象限，
所以2a+3＜1且2a+3＞0,解得a＜-1且a＞-$\frac{3}{2}$，
所以-$\frac{3}{2}$＜a＜-1.(8分)