《2025年节节高大象出版社七年级数学上册华师大版》

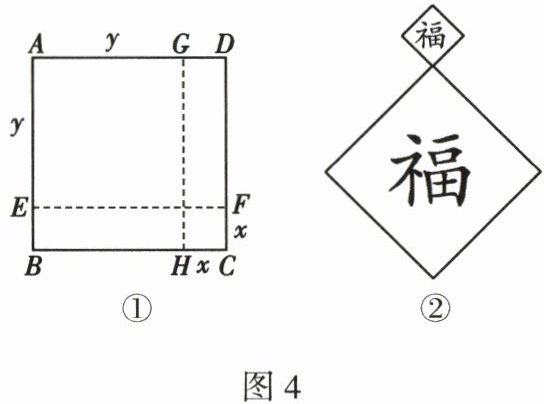
18. （9分）春节贴“福”字是我国由来已久的风俗，它寄托了人们对幸福生活的向往，也是对美好未来的祝愿。如图4①是一张正方形纸片，李明用剪刀沿虚线剪开，制作成如图4②所示的新年挂图。
（1）用含 $x$、$y$ 的代数式表示正方形纸片的周长。
（2）当 $x = 1dm$，$y = 4dm$ 时，求李明剪掉的多余部分的面积。

答案： 18.
(1)由图可得，正方形纸片的边长为y+x，所以这个正方形纸片的周长为4x+4y.
(2)由图可得，剪掉的多余部分的面积为2xy.
当x=1 dm,y=4 dm，则$2xy=2×1×4=8(dm^{2})$.所以剪掉的多余部分的面积为$8dm^{2}$.

19. （9分）定义一种新运算：对任意有理数 $a$，$b$ 都有 $a\oplus b = a - 2b$，例如，$2\oplus 3 = 2 - 2×3 = -4$。
（1）求 $-3\oplus 2$ 的值；
（2）先化简，再求值：$(x - 2y)\oplus (x + 2y)$，其中 $x = -1$，$y = 2$。

答案： 19.
(1)因为$a\oplus b=a-2b$，
所以$-3\oplus2=-3-2×2=-3-4=-7$.
(2)由题意，得
$(x-2y)\oplus(x+2y)=(x-2y)-2(x+2y)=x-2y-2x-4y$
=-x-6y.
当x=-1,y=2时，原式=-(-1)-6×2=1-12=-11.

20. (9分)(1)【数学魔术】
魔术师请观众在心中想好一个数，然后将这个数按图5所示步骤计算，最后将计算结果告诉魔术师，魔术师能立刻说出观众想的那个数。
如果小明想的数是 -2，那么他告诉魔术师的数是-1；
如果小明告诉魔术师的数是 $a$，那么他想的数是a-1。
(2)【魔术创新】
小明对数学魔术很感兴趣，他对小丽说：“请你任意想一个两位数，把这个两位数的十位数字先乘2，再加3，然后把所得的和乘5，最后加上个位数字，把所得的结果告诉我，我就能准确说出你想的那个数。”请用代数式的有关知识解释此魔术的奥秘。

答案： 20.
(1)-1 a-1
(2)设这个两位数为10x+y，
由题意知，(2x+3)×5+y=10x+15+y，
即将所得结果减去15即为原数.