第23页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
4. (2024·德阳)若一个多项式加上$y^{2}+3xy - 4$,结果是$3xy + 2y^{2}-5$,则这个多项式为
y^{2}-1
.
答案:
$4.y^{2}-1$
5. 若用点$A$,$B$,$C$分别表示有理数$a$,$b$,$c$,如图2所示.
(1)判断下列各式的符号:$a + b$
(2)化简:$|a + b|-|c - a|-|c - b|$.
]
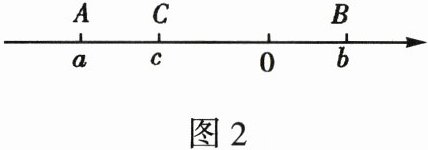
(1)判断下列各式的符号:$a + b$
<
0;$c - a$>
0;$c - b$<
0.(2)化简:$|a + b|-|c - a|-|c - b|$.
]

答案:
5.
(1)< > <【解析】由数轴可得b>0,a<c<0,|a|>|c|>|b|,
所以a+b<0,c-a>0,c-b<0.
(2)|a+b|-|c-a|-|c-b|
=-(a+b)-(c-a)+(c-b)
=-a-b-c+a+c-b=-2b.
(1)< > <【解析】由数轴可得b>0,a<c<0,|a|>|c|>|b|,
所以a+b<0,c-a>0,c-b<0.
(2)|a+b|-|c-a|-|c-b|
=-(a+b)-(c-a)+(c-b)
=-a-b-c+a+c-b=-2b.
6. 已知$A = 2x^{2}+3xy - 4$,$B = x^{2}-xy + 8$.
(1)若$(x - 2)^{2}+|3y - 1| = 0$,求$3A - 6B$的值;
(2)若$3A - 6B$的值与$y$的值无关,求$x$的值.
(1)若$(x - 2)^{2}+|3y - 1| = 0$,求$3A - 6B$的值;
(2)若$3A - 6B$的值与$y$的值无关,求$x$的值.
答案:
6.
(1)因为$(x-2)^{2}+$|3y-1|=0,所以$x=2,y=\frac{1}{3}.$
$3A-6B=3(2x^{2}+3xy-4)-6(x^{2}-xy+8)$
$=6x^{2}+9xy-12-6x^{2}+6xy-48$
=15xy-60.
当$x=2,y=\frac{1}{3}$时,原式$=15×2×\frac{1}{3}-60=10-60=-50.$
(2)由
(1)知3A-6B=15xy-60,
所以当x=0时,3A-6B的值与y的值无关.
(1)因为$(x-2)^{2}+$|3y-1|=0,所以$x=2,y=\frac{1}{3}.$
$3A-6B=3(2x^{2}+3xy-4)-6(x^{2}-xy+8)$
$=6x^{2}+9xy-12-6x^{2}+6xy-48$
=15xy-60.
当$x=2,y=\frac{1}{3}$时,原式$=15×2×\frac{1}{3}-60=10-60=-50.$
(2)由
(1)知3A-6B=15xy-60,
所以当x=0时,3A-6B的值与y的值无关.
7. 为提升居住品质,某小区计划对中庭进行改造,物业规划出一块边长分别是$a$米、$b$米的长方形空地,建设羽毛球场和半圆形儿童乐园两个功能区,剩余部分种植绿植. 设计师给出的方案如图3所示,羽毛球场的边长分别是$m$米、$n$米,儿童乐园的直径是$b$米.
(1)若该空地的面积为300平方米,判断$a$,$b$是否成反比例关系.
(2)小区业主要求该空地改造后有一半以上面积是功能区,若设计师规划的尺寸满足:$a=\frac{3}{2}b$,$m=\frac{1}{2}a$,$n=\frac{1}{2}b$,你认为该设计方案是否符合要求,若符合,请说明理由;若不符合,请给出一个符合要求的设计方案.
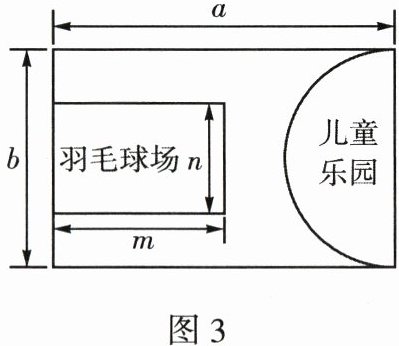
(1)若该空地的面积为300平方米,判断$a$,$b$是否成反比例关系.
(2)小区业主要求该空地改造后有一半以上面积是功能区,若设计师规划的尺寸满足:$a=\frac{3}{2}b$,$m=\frac{1}{2}a$,$n=\frac{1}{2}b$,你认为该设计方案是否符合要求,若符合,请说明理由;若不符合,请给出一个符合要求的设计方案.

答案:
7.
(1)由题意,得ab=300.
因为a、b乘积一定,所以它们成反比例关系.
(2)由题意,得长方形面积为$ab=\frac{3}{2}b^{2},$
羽毛球场的面积为$mn=\frac{1}{2}a·\frac{1}{2}b=\frac{1}{4}·\frac{3}{2}b^{2}=\frac{3}{8}b^{2},$
儿童乐园的面积为$\frac{1}{2}π(\frac{b}{2})^{2}=\frac{1}{8}πb^{2},$
所以功能区的面积为$\frac{3}{8}b^{2}+\frac{1}{8}πb^{2}=(\frac{3}{8}+\frac{1}{8}π)b^{2}.$
因为$\frac{3}{8}+\frac{1}{8}π=\frac{3+π}{8}>\frac{1}{2}×\frac{3}{2},$
所以该设计方案符合要求.
(1)由题意,得ab=300.
因为a、b乘积一定,所以它们成反比例关系.
(2)由题意,得长方形面积为$ab=\frac{3}{2}b^{2},$
羽毛球场的面积为$mn=\frac{1}{2}a·\frac{1}{2}b=\frac{1}{4}·\frac{3}{2}b^{2}=\frac{3}{8}b^{2},$
儿童乐园的面积为$\frac{1}{2}π(\frac{b}{2})^{2}=\frac{1}{8}πb^{2},$
所以功能区的面积为$\frac{3}{8}b^{2}+\frac{1}{8}πb^{2}=(\frac{3}{8}+\frac{1}{8}π)b^{2}.$
因为$\frac{3}{8}+\frac{1}{8}π=\frac{3+π}{8}>\frac{1}{2}×\frac{3}{2},$
所以该设计方案符合要求.
查看更多完整答案,请扫码查看


