第59页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
21. (10分)如图16①,货轮停靠在码头O点,发现灯塔A在它的东北(北偏东45°)方向上,货轮B在码头O的西北方向上.
(1)仿照表示灯塔A方位的方法,画出表示货轮B的方向的射线.
(2)如图16②,两艘货轮从码头O出发,货轮C向东偏北15°的OC方向行驶,货轮D向北偏西15°的OD方向航行,求∠COD的度数.
(3)另有两艘货轮从码头O出发,货轮E向东偏北x°的OE的方向行驶,货轮F向北偏西x°的OF方向航行,请直接用等式表示∠MOE与∠FOQ之间的数量关系:

(1)仿照表示灯塔A方位的方法,画出表示货轮B的方向的射线.
(2)如图16②,两艘货轮从码头O出发,货轮C向东偏北15°的OC方向行驶,货轮D向北偏西15°的OD方向航行,求∠COD的度数.
(3)另有两艘货轮从码头O出发,货轮E向东偏北x°的OE的方向行驶,货轮F向北偏西x°的OF方向航行,请直接用等式表示∠MOE与∠FOQ之间的数量关系:
∠MOE + ∠FOQ = 180°
.
答案:
21.
(1)如图1所示,射线OB的方向就是货轮B所在的方向.


(2)由题意可知,∠MOQ=90°,∠COQ=15°.
所以∠MOC=∠MOQ−∠COQ=75°.
因为∠DOM=15°,
所以∠COD=∠MOC+∠DOM=90°.
(3)∠MOE+∠FOQ=180° [解析]如图2所示,因为∠EOQ=∠MOF=x°,
所以∠EOF=∠MOQ=90°.
因为∠MOP=90°,
所以∠POF=∠MOE.
因为∠POF+∠FOQ=180°,
所以∠MOE+∠FOQ=180°.
21.
(1)如图1所示,射线OB的方向就是货轮B所在的方向.


(2)由题意可知,∠MOQ=90°,∠COQ=15°.
所以∠MOC=∠MOQ−∠COQ=75°.
因为∠DOM=15°,
所以∠COD=∠MOC+∠DOM=90°.
(3)∠MOE+∠FOQ=180° [解析]如图2所示,因为∠EOQ=∠MOF=x°,
所以∠EOF=∠MOQ=90°.
因为∠MOP=90°,
所以∠POF=∠MOE.
因为∠POF+∠FOQ=180°,
所以∠MOE+∠FOQ=180°.
22. (10分)如图17,已知∠AOB = 75°,OC是∠AOB内部的一条射线,过点O作射线OD,使得∠COD = ∠AOB.
(1)若∠AOD = 120°,则∠BOC =
(2)若∠AOD = 5∠BOC,则∠BOD =
(3)当∠COD绕着点O旋转时,∠AOD + ∠BOC是否变化?若不变,求出其大小;若变化,请说明理由.
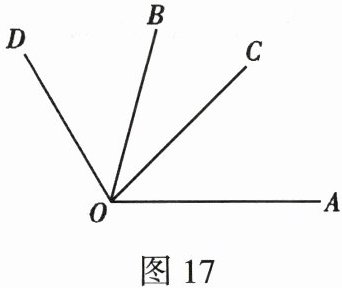
(1)若∠AOD = 120°,则∠BOC =
30
°.(2)若∠AOD = 5∠BOC,则∠BOD =
50
°.(3)当∠COD绕着点O旋转时,∠AOD + ∠BOC是否变化?若不变,求出其大小;若变化,请说明理由.

答案:
22.
(1)30 [解析]因为∠COD=∠AOB,即∠AOC+∠BOC=∠BOC+∠BOD,
所以∠AOC=∠BOD.
因为∠AOD=120°,∠AOB=75°,
所以∠AOC=∠BOD=120°−75°=45°.
所以∠BOC=∠AOB−∠AOC=75°−45°=30°.
(2)50 [解析]设∠BOD=x°,由
(1)得,∠AOC=∠BOD=x°,则∠BOC=75°−x°.
由∠AOD=5∠BOC,得75°+x°=5(75°−x°),解得x=50,即∠BOD=50°.
(3)不变.理由:因为∠COD=∠AOB=75°,∠AOC =∠BOD,
所以∠AOD+∠BOC=∠AOC+∠BOC+∠BOD+∠BOC =∠AOB+∠COD=75°×2=150°.
所以当∠COD绕着点O旋转时,∠AOD+∠BOC=150°,其值不变.
(1)30 [解析]因为∠COD=∠AOB,即∠AOC+∠BOC=∠BOC+∠BOD,
所以∠AOC=∠BOD.
因为∠AOD=120°,∠AOB=75°,
所以∠AOC=∠BOD=120°−75°=45°.
所以∠BOC=∠AOB−∠AOC=75°−45°=30°.
(2)50 [解析]设∠BOD=x°,由
(1)得,∠AOC=∠BOD=x°,则∠BOC=75°−x°.
由∠AOD=5∠BOC,得75°+x°=5(75°−x°),解得x=50,即∠BOD=50°.
(3)不变.理由:因为∠COD=∠AOB=75°,∠AOC =∠BOD,
所以∠AOD+∠BOC=∠AOC+∠BOC+∠BOD+∠BOC =∠AOB+∠COD=75°×2=150°.
所以当∠COD绕着点O旋转时,∠AOD+∠BOC=150°,其值不变.
查看更多完整答案,请扫码查看


