第53页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
17. (12 分)综合与实践。
【主题】卷筒纸的设计与测量
【素材】某品牌卷筒纸,直尺
【实践操作】
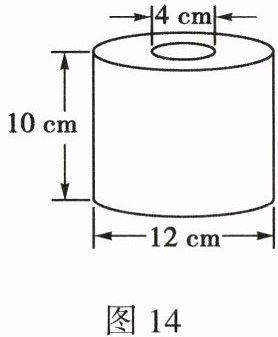
步骤 1:使用直尺测量卷筒纸的高度,中间空心硬纸轴的直径和外层的直径,记录的数据如图 14 所示;
步骤 2:把展开的纸巾折叠多层后再测量,通过计算得到每层纸巾厚度为 $ 0.02\mathrm{cm} $。
【实践探索】
(1)制作这个中间的硬纸轴至少需要多少平方厘米的硬纸板?(用含 $ \pi $ 的代数式表示)
(2)根据以上数据,估计这种规格的一卷空心卷筒纸展开后的总长度。($ \pi $ 的值取 $ 3.14 $)
【主题】卷筒纸的设计与测量
【素材】某品牌卷筒纸,直尺
【实践操作】
步骤 1:使用直尺测量卷筒纸的高度,中间空心硬纸轴的直径和外层的直径,记录的数据如图 14 所示;
步骤 2:把展开的纸巾折叠多层后再测量,通过计算得到每层纸巾厚度为 $ 0.02\mathrm{cm} $。
【实践探索】
(1)制作这个中间的硬纸轴至少需要多少平方厘米的硬纸板?(用含 $ \pi $ 的代数式表示)
(2)根据以上数据,估计这种规格的一卷空心卷筒纸展开后的总长度。($ \pi $ 的值取 $ 3.14 $)

答案:
17.
(1)根据题意,得硬纸轴的直径为4cm,高度为10cm,
所以制作该硬纸轴至少需要硬纸板的面积为4π×10 =40π(cm²).
(2)该卷纸中纸的体积为3.14×[($\frac{12}{2}$)²−($\frac{4}{2}$)²]×10=1004.8(cm³),
该卷纸展开后的总长度为1004.8÷(0.02×10)
=5024(cm).
所以估计这种规格的一卷空心卷筒纸展开后的总长度为5024cm.
(1)根据题意,得硬纸轴的直径为4cm,高度为10cm,
所以制作该硬纸轴至少需要硬纸板的面积为4π×10 =40π(cm²).
(2)该卷纸中纸的体积为3.14×[($\frac{12}{2}$)²−($\frac{4}{2}$)²]×10=1004.8(cm³),
该卷纸展开后的总长度为1004.8÷(0.02×10)
=5024(cm).
所以估计这种规格的一卷空心卷筒纸展开后的总长度为5024cm.
18. (12 分)如图 15,点 $ B $,$ C $,$ D $ 在线段 $ AE $ 上。
(1)图中共有几条线段?说说你分析这个问题的具体思路。
(2)你能用上面的思路来解决“8 位同学参加班上组织的象棋比赛,比赛采用单循环制(即每两位同学之间都要进行一场比赛),那么一共要进行多少场比赛”这个问题吗?

(1)图中共有几条线段?说说你分析这个问题的具体思路。
(2)你能用上面的思路来解决“8 位同学参加班上组织的象棋比赛,比赛采用单循环制(即每两位同学之间都要进行一场比赛),那么一共要进行多少场比赛”这个问题吗?

答案:
18.
(1)因为以点A为左端点向右的线段有线段AB,AC,AD,AE,以点B为左端点向右的线段有线段BC,BD,BE,以点C为左端点向右的线段有线段CD,CE,以点D为左端点的线段有线段DE,所以共有10条线段.
(2)设线段上有m个点,该线段上共有线段x条,则x=(m−1)+(m−2)+(m−3)+…+3+2+1,
所以倒序排列有x=1+2+3+…+(m−3)+(m−2)+(m −1),
所以两式相加得2x=m+m+…+m=m(m−1),
所以x=$\frac{m(m−1)}{2}$.
把8位同学看作直线上的8个点,每两位同学之间的一场比赛看作一条线段,直线上8个点所构成的线段条数就等于比赛的场数,因此一共要进行$\frac{8×(8−1)}{2}$=28场比赛.
(1)因为以点A为左端点向右的线段有线段AB,AC,AD,AE,以点B为左端点向右的线段有线段BC,BD,BE,以点C为左端点向右的线段有线段CD,CE,以点D为左端点的线段有线段DE,所以共有10条线段.
(2)设线段上有m个点,该线段上共有线段x条,则x=(m−1)+(m−2)+(m−3)+…+3+2+1,
所以倒序排列有x=1+2+3+…+(m−3)+(m−2)+(m −1),
所以两式相加得2x=m+m+…+m=m(m−1),
所以x=$\frac{m(m−1)}{2}$.
把8位同学看作直线上的8个点,每两位同学之间的一场比赛看作一条线段,直线上8个点所构成的线段条数就等于比赛的场数,因此一共要进行$\frac{8×(8−1)}{2}$=28场比赛.
查看更多完整答案,请扫码查看


