第65页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
3. (2024·赤峰)将一副三角板(厚度不计)按如图19所示摆放,使有刻度的两条边互相平行,则图中∠1的度数为 (

A.100°
B.105°
C.115°
D.120°
B
)
A.100°
B.105°
C.115°
D.120°
答案:
3.B
4. (2024·陕西)如图20,AB//DC,BC//DE,∠B=145°,则∠D的度数为 (
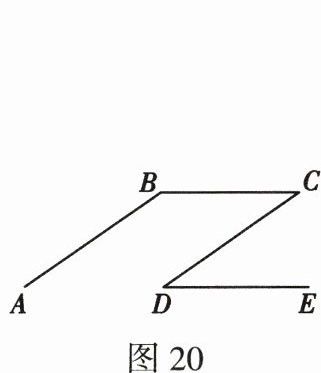
A.25°
B.35°
C.45°
D.55°
B
)
A.25°
B.35°
C.45°
D.55°
答案:
4.B
5. (2024·宁夏)小明与小亮要到科技馆参观,小明家、小亮家和科技馆的方位如图21所示,则科技馆位于小亮家的 (
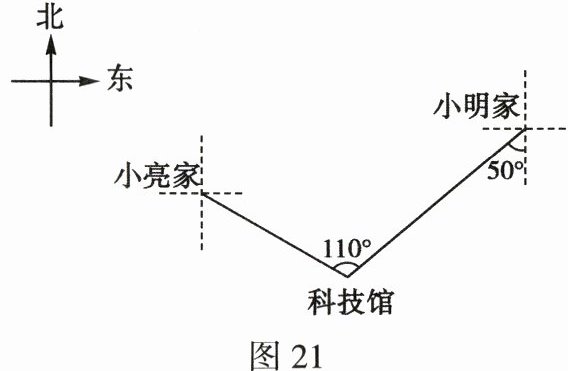
A.南偏东60°方向
B.北偏西60°方向
C.南偏东50°方向
D.北偏西50°方向
A
)
A.南偏东60°方向
B.北偏西60°方向
C.南偏东50°方向
D.北偏西50°方向
答案:
5.A [解析]如图所示,作$CD// AB$,则$\angle ACD = \angle BAC = 50^{\circ}$,

所以$\angle DCE = 110^{\circ} - 50^{\circ} = 60^{\circ}$.
因为$AB// CD$,$AB// EF$,
所以$CD// EF$.
所以$\angle CEF = \angle DCE = 60^{\circ}$.
所以科技馆位于小亮家的南偏东$60^{\circ}$方向.故答案为A.
5.A [解析]如图所示,作$CD// AB$,则$\angle ACD = \angle BAC = 50^{\circ}$,

所以$\angle DCE = 110^{\circ} - 50^{\circ} = 60^{\circ}$.
因为$AB// CD$,$AB// EF$,
所以$CD// EF$.
所以$\angle CEF = \angle DCE = 60^{\circ}$.
所以科技馆位于小亮家的南偏东$60^{\circ}$方向.故答案为A.
6. (2024·潍坊)一种路灯的示意图如图22所示,其底部支架AB与吊线FG平行,灯杆CD与底部支架AB所成锐角α=15°,顶部支架EF与灯杆CD所成锐角β=45°,则EF与FG所成锐角的度数为 (
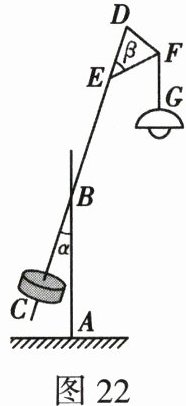
A.60°
B.55°
C.50°
D.45°
A
)
A.60°
B.55°
C.50°
D.45°
答案:
6.A [解析]如图所示,过点$E$作$EH// AB$.

因为$AB// FG$,
所以$AB// EH// FG$.
所以$\angle BEH = \alpha = 15^{\circ}$,$\angle FEH + \angle EFG = 180^{\circ}$.
因为$\beta = 45^{\circ}$,
所以$\angle FEH = 180^{\circ} - 45^{\circ} - 15^{\circ} = 120^{\circ}$.
所以$\angle EFG = 180^{\circ} - \angle FEH = 180^{\circ} - 120^{\circ} = 60^{\circ}$.
所以$EF$与$FG$所成锐角的度数为$60^{\circ}$.
6.A [解析]如图所示,过点$E$作$EH// AB$.

因为$AB// FG$,
所以$AB// EH// FG$.
所以$\angle BEH = \alpha = 15^{\circ}$,$\angle FEH + \angle EFG = 180^{\circ}$.
因为$\beta = 45^{\circ}$,
所以$\angle FEH = 180^{\circ} - 45^{\circ} - 15^{\circ} = 120^{\circ}$.
所以$\angle EFG = 180^{\circ} - \angle FEH = 180^{\circ} - 120^{\circ} = 60^{\circ}$.
所以$EF$与$FG$所成锐角的度数为$60^{\circ}$.
7. (2024·乐山)如图23,两条平行线a、b被第三条直线c所截. 若∠1=60°,那么∠2=
]
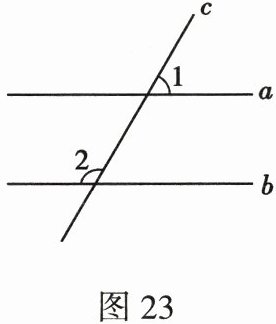
$120^{\circ}$
.]

答案:
7.$120^{\circ}$
8. 如图24,点P在∠AOB中,PM//OB交OA于点M.
(1)过点P作OA的平行线交OB于点N. (利用圆规和无刻度的直尺作图,保留作图痕迹,并标明相应的字母,不写作法)
(2)在(1)的条件下,连接OP,若∠MPO=∠NPO,试说明OP是∠AOB的角平分线.
]
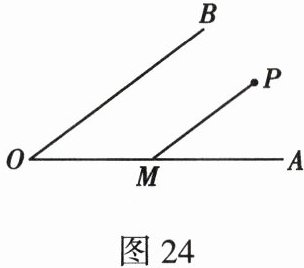
(1)过点P作OA的平行线交OB于点N. (利用圆规和无刻度的直尺作图,保留作图痕迹,并标明相应的字母,不写作法)
(2)在(1)的条件下,连接OP,若∠MPO=∠NPO,试说明OP是∠AOB的角平分线.
]

答案:
8.
(1)如图所示,PN即为所求.

(2)因为$NP// OA$,
所以$\angle NPO = \angle MOP$.
因为$PM// OB$,
所以$\angle MPO = \angle BOP$.
因为$\angle MPO = \angle NPO$,
所以$\angle BOP = \angle MOP$.
所以$OP$平分$\angle AOB$.
8.
(1)如图所示,PN即为所求.

(2)因为$NP// OA$,
所以$\angle NPO = \angle MOP$.
因为$PM// OB$,
所以$\angle MPO = \angle BOP$.
因为$\angle MPO = \angle NPO$,
所以$\angle BOP = \angle MOP$.
所以$OP$平分$\angle AOB$.
查看更多完整答案,请扫码查看


