《2025年节节高大象出版社七年级数学上册华师大版》

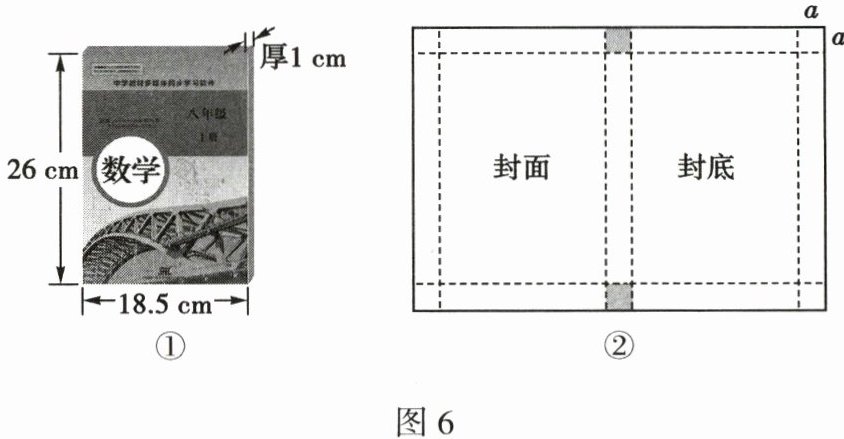
22. （10分）小莹非常喜欢数学，十分爱护数学书，她通常会选用封皮来精心包裹书本。现有一本如图6①所示的数学书，其长为26cm，宽为18.5cm，厚为1cm，小莹用一张长方形纸包好了这本数学书，封皮展开如图6②所示，图中虚线为折痕，阴影是被裁剪掉的部分，四角均为大小相同的正方形，正方形的边长即折进去的宽度为 $a cm$。
（1）求小莹所用包书纸的周长是多少？（用含 $a$ 的代数式表示，并化简）
（2）当封面和封底各折进去的宽度为2cm时，请帮小莹计算一下封皮的展开图面积。

答案： 22.
(1)小莹所用包书纸的周长为：
$2(18.5×2+1+2a)+2(26+2a)=2(38+2a)+2(26+2a)=76+4a+52+4a=8a+128(cm)$.
所以小莹所用包书纸的周长为(8a+128)cm.
(2)当a=2时，包书纸长为$18.5×2+1+2×2=$
42(cm)，包书纸宽为$26+2×2=30(cm)$，
所以封皮的展开图面积为$42×30-4=1256(cm^{2})$.

23. (10分)我们规定：使得 $a - b = ab$ 成立的一对数 $a$，$b$ 为“积差等数对”，记为 $(a, b)$。例如，因为 $1.5 - 0.6 = 1.5×0.6$，$(-2) - 2 = (-2)×2$，所以数对 $(1.5, 0.6)$，$(-2, 2)$ 都是“积差等数对”。
(1)下列数对中，是“积差等数对”的是①③(填序号)；
① $(2, \frac{2}{3})$
② $(1.5, 3)$
③ $(-\frac{1}{2}, -1)$
(2)若 $(m, n)$ 是“积差等数对”，求代数式 $4[4mn - m - 3(mn - 1)] - 2(3m^{2} - 2n) + 6m^{2}$ 的值。

答案： 23.
(1)①③ 【解析】因为$2-\frac{2}{3}=\frac{4}{3}$，$2×\frac{2}{3}=\frac{4}{3}$，
所以$(2,\frac{2}{3})$是“积差等数对”.
因为1.5-3=-1.5,$1.5×3=4.5$，
所以(1.5,3)不是“积差等数对”.
因为$-\frac{1}{2}-(-1)=\frac{1}{2}$，$(-\frac{1}{2})×(-1)=\frac{1}{2}$，
所以$(-\frac{1}{2},-1)$是“积差等数对”.
故答案为①③.
(2)若(m,n)是“积差等数对”，则m-n=mn.
$4[4mn-m-3(mn-1)]-2(3m^{2}-2n)+6m^{2}$
=$4×(4mn-m-3mn+3)-6m^{2}+4n+6m^{2}$
=$4×(mn-m+3)-6m^{2}+4n+6m^{2}$
=$4mn-4m+12-6m^{2}+4n+6m^{2}$
=$4mn-4(m-n)+12$.
因为m-n=mn，
所以原式=$4mn-4mn+12=12$.