第86页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
8. 如图,现测得AB = AD = 26 m,BC = 16 m,CD = 12 m,且BD = 20 m.
(1)试说明:∠BCD = 90°;
(2)求四边形展区(阴影部分)的面积.
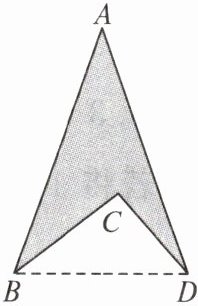
(1)试说明:∠BCD = 90°;
(2)求四边形展区(阴影部分)的面积.

答案:
解:
(1)
∵在△BCD 中,BC=16 m,CD=12 m,BD=20 m,
∴BC²+CD²=16²+12²=400,BD²=20²=400,
∴BC²+CD²=BD²,
∴△BCD 是直角三角形,且∠BCD=90°.
(2)如图,过点 A 作 AE⊥BD 于点 E,

则∠AEB=90°.
∵AB=AD,
∴BE=DE=$\frac{1}{2}$BD=10 m.
在 Rt△ABE 中,AB=26 m,
∴AE=$\sqrt{AB^2-BE^2}=\sqrt{26^2-10^2}$=24(m),
∴S△ABD=$\frac{1}{2}$BD·AE=$\frac{1}{2}$×20×24=240(m²).
∵S△BCD=$\frac{1}{2}$BC·CD=$\frac{1}{2}$×16×12=96(m²),
∴S阴影部分=S△ABD-S△BCD=240-96=144(m²).
解:
(1)
∵在△BCD 中,BC=16 m,CD=12 m,BD=20 m,
∴BC²+CD²=16²+12²=400,BD²=20²=400,
∴BC²+CD²=BD²,
∴△BCD 是直角三角形,且∠BCD=90°.
(2)如图,过点 A 作 AE⊥BD 于点 E,

则∠AEB=90°.
∵AB=AD,
∴BE=DE=$\frac{1}{2}$BD=10 m.
在 Rt△ABE 中,AB=26 m,
∴AE=$\sqrt{AB^2-BE^2}=\sqrt{26^2-10^2}$=24(m),
∴S△ABD=$\frac{1}{2}$BD·AE=$\frac{1}{2}$×20×24=240(m²).
∵S△BCD=$\frac{1}{2}$BC·CD=$\frac{1}{2}$×16×12=96(m²),
∴S阴影部分=S△ABD-S△BCD=240-96=144(m²).
9. (几何直观、推理能力)定义:在△ABC中,若BC = a,AC = b,AB = c,a、b、c满足$ac + a^2 = b^2,$则称这个三角形为“类勾股三角形”. 请根据以上定义解决下列问题:
(1)如图1所示,若等腰三角形ABC是“类勾股三角形”,AB = BC,AC>AB,求∠A的度数;
(2)如图2所示,在△ABC中,∠B = 2∠A,且∠C>∠A,求证:△ABC为“类勾股三角形”. 小明同学想到可以在AB上找一点D使得AD = CD,再作CE⊥BD,请你帮助小明完成证明过程.
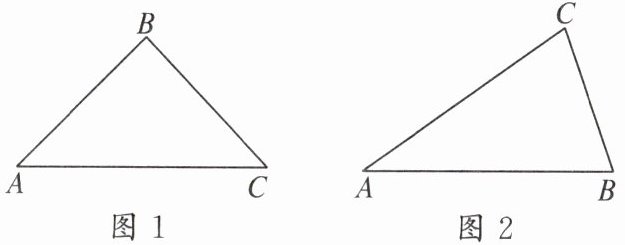
(1)如图1所示,若等腰三角形ABC是“类勾股三角形”,AB = BC,AC>AB,求∠A的度数;
(2)如图2所示,在△ABC中,∠B = 2∠A,且∠C>∠A,求证:△ABC为“类勾股三角形”. 小明同学想到可以在AB上找一点D使得AD = CD,再作CE⊥BD,请你帮助小明完成证明过程.

答案:
解:
(1)
∵AB=BC,AC>AB,
∴a=c,b>c.
∵△ABC 是"类勾股三角形",
∴ac+a²=b²,
∴c²+a²=b²,
∴△ABC 是等腰直角三角形,
∴∠A=45°.
(2)如图,在 AB 上找一点 D,使得 AD=CD,再作 CE⊥BD.

∵AD=CD,
∴∠A=∠ACD,
∴∠CDB=∠ACD+∠A=2∠A.
∵∠B=2∠A,
∴∠CDB=∠B,
∴CD=CB=a,
∴AD=CD=a,
∴DB=AB-AD=c-a.
∵CE⊥AB,
∴DE=BE=$\frac{1}{2}$(c-a),
∴AE=AD+DE=a+$\frac{1}{2}$(c-a)=$\frac{1}{2}$(c+a).
在 Rt△ACE 中,CE²=AC²-AE²=b²-[$\frac{1}{2}$(c+a)]²,
在 Rt△BCE 中,CE²=BC²-BE²=a²-[$\frac{1}{2}$(c-a)]²,
∴b²-[$\frac{1}{2}$(c+a)]²=a²-[$\frac{1}{2}$(c-a)]²,
∴b²=ac+a²,
∴△ABC 是"类勾股三角形".
解:
(1)
∵AB=BC,AC>AB,
∴a=c,b>c.
∵△ABC 是"类勾股三角形",
∴ac+a²=b²,
∴c²+a²=b²,
∴△ABC 是等腰直角三角形,
∴∠A=45°.
(2)如图,在 AB 上找一点 D,使得 AD=CD,再作 CE⊥BD.

∵AD=CD,
∴∠A=∠ACD,
∴∠CDB=∠ACD+∠A=2∠A.
∵∠B=2∠A,
∴∠CDB=∠B,
∴CD=CB=a,
∴AD=CD=a,
∴DB=AB-AD=c-a.
∵CE⊥AB,
∴DE=BE=$\frac{1}{2}$(c-a),
∴AE=AD+DE=a+$\frac{1}{2}$(c-a)=$\frac{1}{2}$(c+a).
在 Rt△ACE 中,CE²=AC²-AE²=b²-[$\frac{1}{2}$(c+a)]²,
在 Rt△BCE 中,CE²=BC²-BE²=a²-[$\frac{1}{2}$(c-a)]²,
∴b²-[$\frac{1}{2}$(c+a)]²=a²-[$\frac{1}{2}$(c-a)]²,
∴b²=ac+a²,
∴△ABC 是"类勾股三角形".
查看更多完整答案,请扫码查看


