第83页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
1. 求几何体表面两点之间的最短路径,通常将几何体的表面展开,把立体图形转化为平面图形,然后利用“
两点之间,线段最短
”进行解决.
答案:
两点之间,线段最短
2. 解决放置问题或通过问题的关键是构造
直角三角形
,然后通过比较所得结果与实际数值做出判断.
答案:
直角三角形
3. 运用勾股定理和判定直角三角形的勾股定理的逆定理解决实际问题,解决问题的关键是构造
直角三角形
.
答案:
直角三角形
【典例1】小彬用3D打印机制作了一个底面周长为30 cm,高为20 cm的圆柱粮仓模型,如图,BC是底面直径,AB是高. 现要在此模型的侧面贴一圈彩色装饰带,使装饰带经过A、C两点(接头不计),则装饰带的长度最短为______.
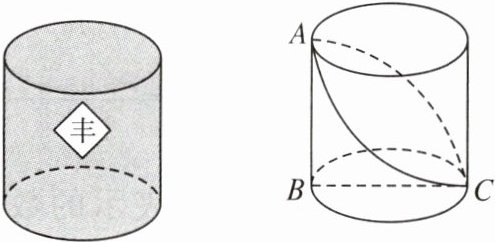

答案:
解析:如图是圆柱的侧面展开图,它是一个矩形,AB = A'B' = 20 cm,BC = B'C = $\frac{1}{2}$×30 = 15(cm).
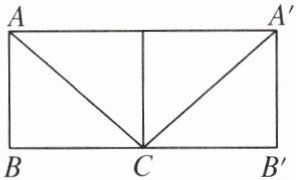
∵∠B = ∠B' = 90°,
∴AC = A'C = $\sqrt{20^{2}+15^{2}}$ = 25(cm),
∴AC + A'C = 25 + 25 = 50(cm),
∴装饰带的长度最短为50 cm.
解析:如图是圆柱的侧面展开图,它是一个矩形,AB = A'B' = 20 cm,BC = B'C = $\frac{1}{2}$×30 = 15(cm).

∵∠B = ∠B' = 90°,
∴AC = A'C = $\sqrt{20^{2}+15^{2}}$ = 25(cm),
∴AC + A'C = 25 + 25 = 50(cm),
∴装饰带的长度最短为50 cm.
1. 如图,棱柱的底面是边长为4的正方形,侧面都是长为8的长方形,点D是BC的中点,在棱柱下底面的A点处有一只蚂蚁,它想吃到上底面点D处的食物,需要爬行的最短路程是s,则$s^2$的值为(
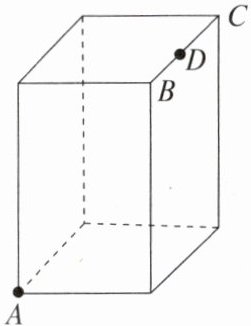
A.196
B.116
C.100
D.84
C
)
A.196
B.116
C.100
D.84
答案:
C
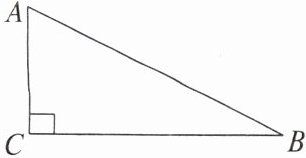
【典例2】如图,从台阶的下端点B到上端点A的直线距离为(
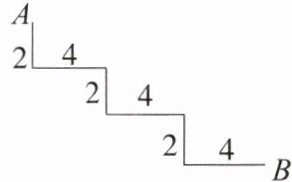
A.$\sqrt{150}$
B.$\sqrt{180}$
C.$\sqrt{200}$
D.$\sqrt{208}$
B
)

A.$\sqrt{150}$
B.$\sqrt{180}$
C.$\sqrt{200}$
D.$\sqrt{208}$
答案:
解析:根据题意,得AC = 2 + 2 + 2 = 6,BC = 4 + 4 + 4 = 12,根据勾股定理,得AB = $\sqrt{AC^{2}+BC^{2}}$ = $\sqrt{6^{2}+12^{2}}$ = $\sqrt{180}$.
B
B
查看更多完整答案,请扫码查看


