《2025年配套综合练习甘肃八年级数学上册华师大版》

1. 角边角基本事实
如果两个三角形有两个角及其夹边分别对应相等,那么这两个三角形全等.
简记为“ASA”或“角边角”.

答案： ASA

2. 角角边定理
如果两个三角形有两个角及一个角的对边分别对应相等,那么这两个三角形全等.
简记为“AAS”或“角角边”.

答案： AAS

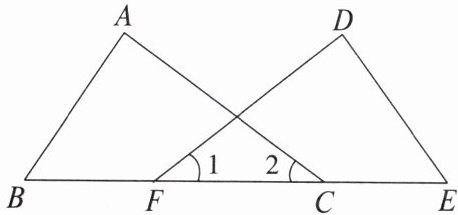
【典例1】如图,点B、F、C、E在同一直线上,AC= DF,∠1= ∠2. 如果根据“ASA”判断△ABC≌△DEF,那么需要补充的条件是(B)

A.AB= DE
B.∠A= ∠D
C.BF= CE
D.∠B= ∠E

答案： 解析：需要补充的条件是∠A= ∠D,
在△ABC和△DEF中,$\left\{\begin{array}{l} ∠A= ∠D,\\ AC= DF,\\ ∠2= ∠1,\end{array} \right.$
∴△ABC≌△DEF(ASA).
B

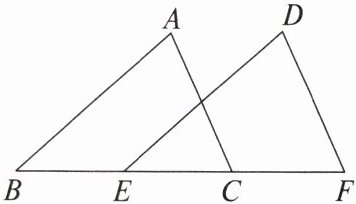
1. 如图,已知AB//DE,AB= DE,请你添加一个条件∠A=∠D(答案不唯一),使△ABC≌△DEF.

答案： ∠A=∠D(答案不唯一)

【典例2】在△ABC和△EMN中,已知∠A= 50°,∠B= 60°,∠E= 70°,∠M= 60°,AC= EN,则这两个三角形(A)
A.一定全等
B.一定不全等
C.不一定全等
D.以上都不对

答案： 解析：
∵∠A= 50°,∠B= 60°,
∴∠C= 70°.
在△ABC和△NME中,
$\left\{\begin{array}{l} ∠B= ∠M,\\ ∠C= ∠E,\\ AC= EN,\end{array} \right.$
∴△ABC≌△NME(AAS).
A

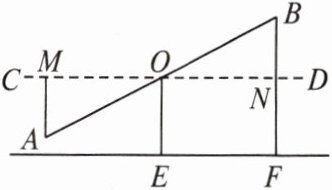
2. 如图是一个跷跷板的示意图,点O是跷跷板AB的中点,支柱OE与地面垂直,且OE的长度为50 cm. 当点A到水平线CD的距离AM为40 cm时,求点B到地面的距离.

答案： 解:在△OAM与△OBN中，
∠AMO=∠BNO=90°,
∠AOM=∠BON,
OA=OB,
∴△OAM≌△OBN(AAS),
∴BN=AM=40cm,
∴点B到地面的距离为50+40=90(cm).
答:点B到地面的距离为90cm.