《2025年配套综合练习甘肃八年级数学上册华师大版》

14. (8分)某金属冶炼厂将 $ 27 $ 块大小相同的正方体钢铁在炉火中熔化,重新铸成一块新的长方体钢铁,且此长方体的长、宽、高分别为 $ 16 \mathrm{~dm}、4 \mathrm{~dm} $ 和 $ 8 \mathrm{~dm} $,求原来每块正方体钢铁的棱长.(不计损耗)

答案： 解:根据题意得原来每个正方体钢铁的体积为16×4×8÷27=$\frac{512}{27}$(dm$^{3}$),则原来每个正方体钢铁的棱长为$\sqrt[3]{\frac{512}{27}}=\frac{8}{3}$(dm),即原来每个正方体钢铁的棱长为$\frac{8}{3}$dm.

15. (10分)如图,数轴上从左至右依次有 $ C、O、A、B $ 四个点,分别对应的数字为 $ x、0、1 $ 和 $ \sqrt{3} $,且 $ AB= CO $.
(1)求 $ AB $ 的长和 $ x $ 的值;
(2)求 $ (x+\sqrt{3})^2 $ 的平方根.

答案： 解:
(1)
∵A,B对应的数字分别为1和$\sqrt{3}$,
∴AB=$\sqrt{3}-1$,
∵C,O对应的数字分别为x,0,
∴CO=0-x=-x.
∵AB=CO,
∴$\sqrt{3}-1=-x$,
∴x=1-$\sqrt{3}$.
(2)当x=1-$\sqrt{3}$时,(x+$\sqrt{3}$)$^{2}$=(1-$\sqrt{3}+\sqrt{3}$)$^{2}$=1$^{2}$=1,
∵1的平方根是±1,
∴(x+$\sqrt{3}$)$^{2}$的平方根是±1.

16. (10分)已知 $ 3a-2 $ 的立方根是 $ -2 $,$ 2a+b-1 $ 的算术平方根是 $ 2 $,$ c $ 是 $ -2 $ 的相反数.
(1)求 $ a、b、c $ 的值;
(2)求 $ a+b+c $ 的平方根.

答案： 解:
(1)
∵3a-2的立方根是-2,
∴3a-2=(-2)$^{3}$=-8,解得a=-2.
∵2a+b-1的算术平方根是2,
∴2a+b-1=2$^{2}$=4,即-4+b-1=4,解得b=9.
∵c是-2的相反数,
∴c=2,
∴a=-2,b=9,c=2.
(2)
∵a=-2,b=9,c=2,
∴a+b+c=-2+9+2=9,
∴a+b+c的平方根为±3.

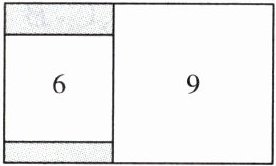
17. (12分)如图,长方形内有两个相邻的正方形,面积分别为 $ 9 $ 和 $ 6 $.
(1)小正方形边长的值在哪两个连续的整数之间? 与哪个整数较接近?(直接写结果)
(2)求图中阴影部分的面积.
(3)若小正方形边长的值的整数部分为 $ x $,小数部分为 $ y $,求 $ (y-\sqrt{6})^x $ 的值.

答案： 解:
(1)
∵小正方形的面积为6,
∴小正方形的边长为$\sqrt{6}$.
∵4＜6＜9,
∴2＜$\sqrt{6}$＜3,
∴小正方形的边长在2和3之间;与整数2比较接近.
(2)
∵阴影部分的面积为一个长为$\sqrt{6}$,宽为(3-$\sqrt{6}$)的长方形的面积,
∴阴影部分的面积=$\sqrt{6}$×(3-$\sqrt{6}$)=3$\sqrt{6}-6$.
(3)
∵小正方形的边长为$\sqrt{6}$,
∴x=2,y=$\sqrt{6}-2$,
∴原式=($\sqrt{6}-2-\sqrt{6}$)$^{2}$=4.