第6页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
4. 把下列各数填入相应的集合内:
$-8,6,\sqrt{5},\sqrt{\frac{3}{2}},\frac{17}{9},\sqrt[3]{-64},-\pi,0.76$.
(1)有理数集合:{
(2)无理数集合:{
$-8,6,\sqrt{5},\sqrt{\frac{3}{2}},\frac{17}{9},\sqrt[3]{-64},-\pi,0.76$.
(1)有理数集合:{
$-8,6,\frac{17}{9},\sqrt[3]{-64},0.76$
…};(2)无理数集合:{
$\sqrt{5},\sqrt{\frac{3}{2}},-\pi$
…}.
答案:
(1)有理数集合:{$-8,6,\frac{17}{9},\sqrt[3]{-64},0.76$…};
(2)无理数集合:{$\sqrt{5},\sqrt{\frac{3}{2}},-\pi$…}。
(1)有理数集合:{$-8,6,\frac{17}{9},\sqrt[3]{-64},0.76$…};
(2)无理数集合:{$\sqrt{5},\sqrt{\frac{3}{2}},-\pi$…}。
1. 在实数 $0,-\frac{1}{2},3.14,\sqrt{5}$中,属于无理数的是(
A.0
B.$-\frac{1}{2}$
C.3.14
D.$\sqrt{5}$
D
)A.0
B.$-\frac{1}{2}$
C.3.14
D.$\sqrt{5}$
答案:
D
2. 下列说法中正确的是(
A.带根号的数是无理数
B.无限小数是无理数
C.无理数就是开方开不尽的数
D.无理数是无限不循环小数
D
)A.带根号的数是无理数
B.无限小数是无理数
C.无理数就是开方开不尽的数
D.无理数是无限不循环小数
答案:
D
3. 下列说法中,正确的是(
A.有理数都是有限小数
B.无限小数就是无理数
C.实数包括有理数、无理数和零
D.无论是有理数还是无理数,都可以用数轴上的点来表示
D
)A.有理数都是有限小数
B.无限小数就是无理数
C.实数包括有理数、无理数和零
D.无论是有理数还是无理数,都可以用数轴上的点来表示
答案:
D
4. 如图,数轴上表示 $\sqrt{2}$ 的点是(
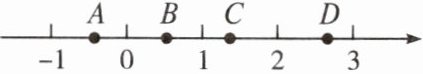
A.点 $A$
B.点 $B$
C.点 $C$
D.点 $D$
C
)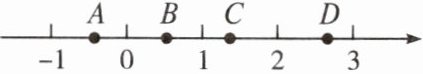
A.点 $A$
B.点 $B$
C.点 $C$
D.点 $D$
答案:
C
5. 已知 $43^{2}= 1 849,44^{2}= 1 936,45^{2}= 2 025,46^{2}= 2 116$. 若 $n$ 为整数,且 $n\lt\sqrt{2 024}\lt n + 1$,则 $n$ 的值为(
A.43
B.44
C.45
D.46
B
)A.43
B.44
C.45
D.46
答案:
B
6. 在实数 $8,0.808 008 000 8…$(每两个 $8$ 之间 $0$ 的个数逐次加 1),$-\sqrt{8},\sqrt[3]{8},-\frac{1}{8},\frac{8}{9}$中,整数有
8,∛8
;分数有-1/8,8/9
;无限小数有0.8080080008…,-√8,8/9
;有理数有8,∛8,-1/8,8/9
;无理数有0.8080080008…,-√8
.
答案:
整数有8,∛8;分数有-1/8,8/9;无限小数有0.8080080008…,-√8,8/9;有理数有8,∛8,-1/8,8/9;无理数有0.8080080008…,-√8。
7. 计算:
(1)$\sqrt{4}-\sqrt[3]{8}+\sqrt[3]{-\frac{1}{27}}$;
(2)$-1^{4}-2×(-3)^{2}+\sqrt[3]{-27}÷(-\frac{1}{3})$.
(1)$\sqrt{4}-\sqrt[3]{8}+\sqrt[3]{-\frac{1}{27}}$;
(2)$-1^{4}-2×(-3)^{2}+\sqrt[3]{-27}÷(-\frac{1}{3})$.
答案:
(1)
$\sqrt{4} - \sqrt[3]{8} + \sqrt[3]{-\frac{1}{27}}$
$ = 2 - 2 + (-\frac{1}{3}) $
$= -\frac{1}{3}$
(2)
$-1^{4} - 2 × (-3)^{2} + \sqrt[3]{-27} ÷ (-\frac{1}{3})$
$ = -1 - 2 × 9 + (-3) ÷ (-\frac{1}{3}) $
$= -1 - 18 + 9 $
$= -10$
(1)
$\sqrt{4} - \sqrt[3]{8} + \sqrt[3]{-\frac{1}{27}}$
$ = 2 - 2 + (-\frac{1}{3}) $
$= -\frac{1}{3}$
(2)
$-1^{4} - 2 × (-3)^{2} + \sqrt[3]{-27} ÷ (-\frac{1}{3})$
$ = -1 - 2 × 9 + (-3) ÷ (-\frac{1}{3}) $
$= -1 - 18 + 9 $
$= -10$
8. (运算能力)定义:已知 $a、b$ 都是实数,若 $a + b = 3$,则称 $a$ 与 $b$ 是关于 $3$ 的“实验数”.
(1)$4$ 与

(2)若 $m= \sqrt{2}-6$,判断 $m$ 与 $9-\sqrt{2}$ 是不是关于 $3$ 的“实验数”,并说明理由.
(2)m与9-√2是关于3的“实验数”.理由如下:
∵√2-6+9-√2=√2-√2+9-6=3,
∴m与9-√2是关于3的“实验数”.
(1)$4$ 与
-1
是关于 $3$ 的“实验数”,$\sqrt{2}$与 $y$ 是关于 $3$ 的“实验数”,则 $y$ 是3-√2
,表示 $y$ 的值的点落在数轴上的位置位于④
.
(2)若 $m= \sqrt{2}-6$,判断 $m$ 与 $9-\sqrt{2}$ 是不是关于 $3$ 的“实验数”,并说明理由.
(2)m与9-√2是关于3的“实验数”.理由如下:
∵√2-6+9-√2=√2-√2+9-6=3,
∴m与9-√2是关于3的“实验数”.
答案:
(1)-1,3-√2,④
(2)m与9-√2是关于3的“实验数”.理由如下:
∵√2-6+9-√2=√2-√2+9-6=3,
∴m与9-√2是关于3的“实验数”.
(1)-1,3-√2,④
(2)m与9-√2是关于3的“实验数”.理由如下:
∵√2-6+9-√2=√2-√2+9-6=3,
∴m与9-√2是关于3的“实验数”.
查看更多完整答案,请扫码查看


