《2025年配套综合练习甘肃八年级数学上册华师大版》

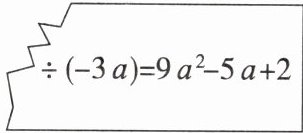
5. 如图,调皮的弟弟把小雅的作业本撕掉了一角,留下一道残缺不全的题目,请你帮她推测出被除式等于-27a³+15a²-6a。

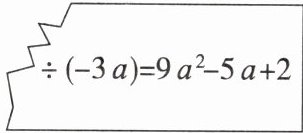
答案： -27a³+15a²-6a

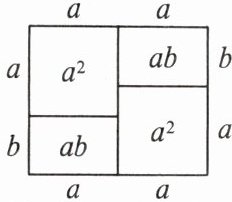
6. 通过计算几何图形的面积可表示一些代数恒等式(一定成立的等式),请根据图写出一个代数恒等式：2a(a+b)=2a²+2ab。

答案： 2a(a+b)=2a²+2ab

7. 计算：(1) $2a^{2}b\cdot(\frac{1}{2}ab - 3ab^{2})$；
(2) $(\frac{1}{3}x-\frac{3}{4}xy)\cdot(-12y)$。

答案： 7. 解:
(1)原式=2a²b·$\frac{1}{2}$ab+2a²b·(-3ab²)=a³b²-6a³b³.
(2)原式=$\frac{1}{3}$x·(-12y)+($-\frac{3}{4}$xy)·(-12y)=-4xy+9xy².

8. (1) 解不等式：$2x(x - 1)-x(2x - 5)＜12$。
(2) 解方程：$x(2x - 4)+3x(x - 1)= 5x(x - 3)+8$。

答案： 8. 解:
(1)去括号,得2x²-2x-2x²+5x＜12，
合并同类项,得3x＜12，
系数化为1,得x＜4.
(2)去括号,得2x²-4x+3x²-3x=5x²-15x+8，
合并同类项,得5x²-7x=5x²-15x+8，
移项,合并同类项,得8x=8，
系数化为1,得x=1.

9. 一块长方形的铁皮,长为 $(5a^{2}+4b^{2})$ 米,宽为 $6a^{2}$ 米,在它的四个角上都剪出一个边长为 $a^{2}$ 米的小正方形,然后拼成一个无盖的盒子,问盒子的表面积是多少？

答案： 9. 解:(5a²+4b²)×6a²-4a²×a²=30a⁴+24a²b²-4a⁴=26a⁴+24a²b².
答:盒子的表面积为(26a⁴+24a²b²)平方米.

10.(运算能力)某同学在计算一个多项式乘 $-3x^{2}$ 时,因抄错运算符号,算成了加上 $-3x^{2}$,得到的结果是 $x^{2}-4x + 1$,那么正确的计算结果是多少？

答案： 10. 解:由题意可得,原多项式为x²-4x+1-(-3x²)=4x²-4x+1，
则计算正确的结果为:-3x²×(4x²-4x+1)=-12x⁴+12x³-3x².