第77页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
【典例3】《九章算术》中记载了一个“折竹抵地”问题:今有竹高一丈,末折抵地,去本三尺,问折者高几何?题意是:一根竹子原高1丈(1丈 = 10尺),中部有一处折断,竹梢触地面处离竹根3尺,试问折断处离地面多高?设折断处离地面的高度为$x$尺,则可列方程为(
A.$x^{2}-3= (10 - x)^{2}$
B.$x^{2}-3^{2}= (10 - x)^{2}$
C.$x^{2}+3= (10 - x)^{2}$
D.$x^{2}+3^{2}= (10 - x)^{2}$
D
)A.$x^{2}-3= (10 - x)^{2}$
B.$x^{2}-3^{2}= (10 - x)^{2}$
C.$x^{2}+3= (10 - x)^{2}$
D.$x^{2}+3^{2}= (10 - x)^{2}$
答案:
解析:根据折断处离地面的高度为$x$尺,可得$x^{2}+3^{2}= (10 - x)^{2}$。
D
D
3. 如图,台风过境后,一根垂直于地面的大树在离地面6m处断裂,大树顶部落在离大树底部8m处,则大树折断之前的高度是(
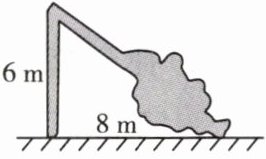
A.10m
B.14m
C.16m
D.18m
C
)
A.10m
B.14m
C.16m
D.18m
答案:
C
【典例4】如图,长方体木箱的长、宽、高分别为12cm、4cm、3cm,则能放进木箱中的木棒最长为(
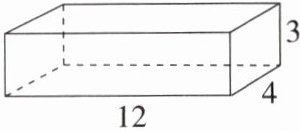
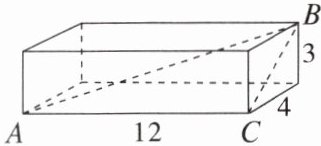
A.19cm
B.24cm
C.13cm
D.15cm
C
)

A.19cm
B.24cm
C.13cm
D.15cm
答案:
解析:$\because侧面对角线BC^{2}= 3^{2}+4^{2}= 5^{2}$,$\therefore CB = 5cm$。
$\because AC = 12cm$,$\angle ACB = 90^{\circ}$,
$\therefore AB= \sqrt{12^{2}+5^{2}} = 13(cm)$,
$\therefore$能放进木箱中的木棒最长为13cm。
C
$\because AC = 12cm$,$\angle ACB = 90^{\circ}$,
$\therefore AB= \sqrt{12^{2}+5^{2}} = 13(cm)$,
$\therefore$能放进木箱中的木棒最长为13cm。
C
4. 如图,一支长为15cm的铅笔放在长方体笔筒中,已知笔筒的三边长度依次为3cm、4cm、12cm,那么这支铅笔露在笔筒外的部分长度$x$的范围是(
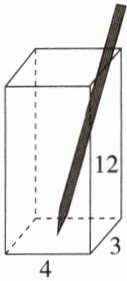
A.$2cm\leqslant x\leqslant5cm$
B.$2cm\leqslant x\leqslant3cm$
C.$4cm\leqslant x\leqslant5cm$
D.$9cm\leqslant x\leqslant12cm$
B
)
A.$2cm\leqslant x\leqslant5cm$
B.$2cm\leqslant x\leqslant3cm$
C.$4cm\leqslant x\leqslant5cm$
D.$9cm\leqslant x\leqslant12cm$
答案:
B
1. 在$Rt\triangle ABC$中,$\angle C = 90^{\circ}$,$AC = 3$,$AB = 5$,则$BC = $(
A.$\sqrt{34}$
B.8
C.2
D.4
D
)A.$\sqrt{34}$
B.8
C.2
D.4
答案:
D
2. 如图,直线$AO\perp OB$,垂足为$O$,线段$AO = 3$,$BO = 4$,以点$A$为圆心,$AB$的长为半径画弧,交直线$AO于点C$。则$OC$的长为(
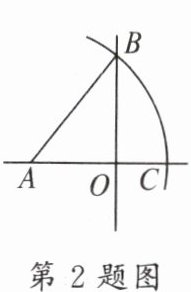
A.5
B.4
C.3
D.2
D
)
A.5
B.4
C.3
D.2
答案:
D
查看更多完整答案,请扫码查看


