《2025年配套综合练习甘肃八年级数学上册华师大版》

3. 下面命题中是定义的是(A)
A.像$3$,$3.5$,$500$,$1.2$这样的数是正数
B.西红柿是红色的
C.绝对值具有非负性
D.对顶角相等

答案： A

4. “两条平行直线被第三条直线所截,同位角相等”这句话是(C)
A.假命题
B.定义
C.基本事实
D.定理

答案： C

5. 已知$\angle 1+\angle 2 = 90^{\circ}$,$\angle 3+\angle 4 = 90^{\circ}$,如果$\angle 1= \angle 3$,那么$\angle 2= \angle 4$,依据是(C)
A.同角的余角相等
B.同角的补角相等
C.等角的余角相等
D.等角的补角相等

答案： C

6. 能说明命题“对于任意实数$a$,都有$\vert a\vert＞0$”是假命题的反例是(C)
A.$a = -2$
B.$a = 1$
C.$a = 0$
D.$a = \sqrt{9}$

答案： C

7. 下列语句是命题的是③④(填序号)。
①你对本节课掌握得怎么样？②队伍前进$200m$。③全等三角形的对应角相等。④三条直线两两相交有一个或三个交点。

答案： ③④

8. 命题“绝对值相等的两个数互为相反数”。写成“如果……,那么……”的形式为如果两个数的绝对值相等，那么这两个数互为相反数。。

答案： 如果两个数的绝对值相等，那么这两个数互为相反数。

9. 判断下列命题是真命题,还是假命题,是假命题的举反例加以说明。
(1) 如果$AB = 2BC$,那么点$C是AB$的中点；
(2) 三条线段分别为$a$,$b$,$c$,如果$a + b＞c$,那么这三条线段一定能组成三角形；
(3) 三角形的内角和等于$180^{\circ}$；
(4) 如果$\vert a\vert=\vert b\vert$,那么$a = b$。

答案：
(4)该命题假命题,如:当a=2,b=-2时,|a|=|b|,但a≠b.

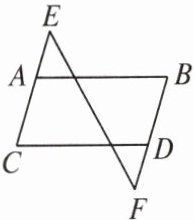
10. (几何直观、推理能力)如图,现有以下三个条件：①$AB// CD$,②$\angle B= \angle C$,③$\angle E= \angle F$。请你以其中两个作为条件,另一个作为结论构造命题。
(1) 你构造的是哪几个命题？
(2) 你构造的命题有真命题吗？若有真命题,请给予证明。

答案： 解:
(1)命题一:如果AB//CD,∠B=∠C,那么∠E=∠F;命题二:如果AB//CD,∠E=∠F,那么∠B=∠C;命题三:如果∠B=∠C,∠E=∠F,那么AB//CD.
(2)命题一是真命题.证明如下:
∵AB//CD,
∴∠B+∠BDC=180°.
∵∠B=∠C,
∴∠C+∠BDC=180°,
∴EC//BF,
∴∠E=∠F.命题二是真命题.证明如下:
∵∠E=∠F,
∴EC//BF,
∴∠C+∠BDC=180°.
∵AB//CD,
∴∠B+∠BDC=180°,
∴∠B=∠C.命题三是真命题.证明如下:
∵∠E=∠F,
∴EC//BF,
∴∠C+∠BDC=180°.
∵∠B=∠C,
∴∠B+∠BDC=180°,
∴AB//CD.