《2025年配套综合练习甘肃八年级数学上册华师大版》

8. 如图，在△ABC 中，∠C = 90°，∠B = 30°，以点 A 为圆心，任意长为半径画弧分别交 AB、AC 于点 M 和 N，再分别以点 M、N 为圆心，大于$\frac{1}{2}$MN 的长为半径画弧，两弧交于点 P，连结 AP 并延长交 BC 于点 D. 给出下列说法：①AD 是△ABC 的角平分线；②∠ADC = 60°；③点 D 在 AB 的垂直平分线上；④$S_{\triangle DAC}:S_{\triangle ABC} = 1:3$. 其中正确的说法有（）

A.1 个
B.2 个
C.3 个
D.4 个

答案： D

9. 如图,已知 $\triangle ABC\cong\triangle DEF$,点 $B$、$E$、$C$、$F$ 依次在同一条直线上。若 $BC = 8$,$CE = 5$,则 $CF$ 的长为3。

答案： 3

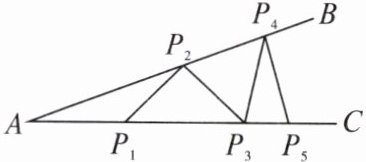
10. 如图,某钢架中,$\angle A = 20^{\circ}$,焊上等长的钢条 $P_{1}P_{2}$、$P_{2}P_{3}$、$P_{3}P_{4}$、$P_{4}P_{5}$ 来加固钢架。如果 $P_{1}A = P_{1}P_{2}$,那么 $\angle BP_{4}P_{5}$ 的度数是100$^{\circ}$。

答案： 100

11. 如图,在 $\triangle ABC$ 中,$AB = AC$,$AD$ 是 $\triangle ABC$ 的角平分线,$DE\perp AB$,$DF\perp AC$,垂足分别是点 $E$、$F$。给出下面结论:①$DA$ 平分 $\angle EDF$；②$AE = AF$,$DE = DF$；③$AD$ 上的点到 $B$、$C$ 两点的距离相等；④图中共有 3 对全等三角形。其中正确的结论是①②③④。(填序号)

答案： ①②③④

12. 命题“如果 $a = b$,那么 $a^{2}= b^{2}$”的逆命题是如果$a^{2}=b^{2}$,那么$a=b$,该命题是假命题(填“真”或“假”)。

答案： 如果$a^{2}=b^{2}$,那么$a=b$　假

13. (12 分)(1)写出下面命题的逆命题,并判断原命题与逆命题的真假。
若两个角相加等于 $180^{\circ}$,则这两个角互为邻补角。
(2)政府准备为三个村庄 $A$、$B$、$C$(其位置如图所示)修建一口水井,要求水井到三个村庄的距离相等,水井应该修在什么地方呢？你能找到吗？(写出作法,并保留作图痕迹)

答案：
解:
(1)若两个角相加等于$180^{\circ}$,则这两个角互为邻补角.它的逆命题是若两个角互为邻补角，则两个角相加等于$180^{\circ}$,逆命题是真命题，原命题是假命题.
(2)作法:如图,①连结AB、BC.
②作AB、BC的垂直平分线，交于点P.则点P就是水井的位置.