第69页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
1. 如图,$OP平分\angle AOB$,$PC\perp OA$,$PD\perp OB$,垂足分别是$C$、$D$,下列结论中错误的是(
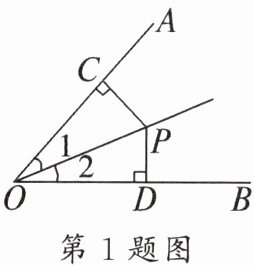
A.$PC = PD$
B.$OC = OD$
C.$\angle CPO= \angle DPO$
D.$OC = PC$
D
)
A.$PC = PD$
B.$OC = OD$
C.$\angle CPO= \angle DPO$
D.$OC = PC$
答案:
D
2. 如图,$BM是\angle ABC$的平分线,点$Q$、$D分别在BA$、$BM$上,点$P为直线BC$上的一个动点.如果$BQ = 6$,$\triangle BDQ的面积为9$,那么线段$DP$的长不可能是(
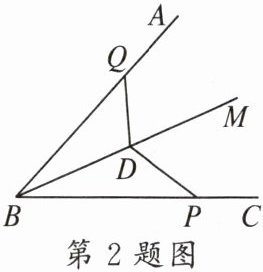
A.$2$
B.$3$
C.$4$
D.$5.5$
A
)
A.$2$
B.$3$
C.$4$
D.$5.5$
答案:
A
3. 如图,$l_{1}$、$l_{2}$、$l_{3}$是三条两两相交的笔直公路,现欲修建一个加油站,使它到三条公路的距离相等,则可供选择的地址有(

A.$1$处
B.$2$处
C.$3$处
D.$4$处
D
)
A.$1$处
B.$2$处
C.$3$处
D.$4$处
答案:
D
4. 三条公路将$A$、$B$、$C$三个村庄连成一个如图所示的三角形区域,如果在这个区域内修建一个集贸市场,要使集贸市场到三条公路的距离相等,那么这个集贸市场应建的位置是(

A.三条高线的交点
B.三条中线的交点
C.三条角平分线的交点
D.三边垂直平分线的交点
C
)
A.三条高线的交点
B.三条中线的交点
C.三条角平分线的交点
D.三边垂直平分线的交点
答案:
C
5. 如图,在$\triangle ABC$中,$\angle C = 90^{\circ}$,$O为\triangle ABC$的三条角平分线的交点,$OD\perp BC$,$OE\perp AC$,$OF\perp AB$,点$D$、$E$、$F$分别是垂足,且$AB = 10\mathrm{cm}$,$BC = 8\mathrm{cm}$,$CA = 6\mathrm{cm}$,则点$O到三边AB$、$AC和BC$的距离分别为(

A.$2\mathrm{cm}$、$2\mathrm{cm}$、$2\mathrm{cm}$
B.$3\mathrm{cm}$、$3\mathrm{cm}$、$3\mathrm{cm}$
C.$4\mathrm{cm}$、$4\mathrm{cm}$、$4\mathrm{cm}$
D.$2\mathrm{cm}$、$3\mathrm{cm}$、$5\mathrm{cm}$
A
)
A.$2\mathrm{cm}$、$2\mathrm{cm}$、$2\mathrm{cm}$
B.$3\mathrm{cm}$、$3\mathrm{cm}$、$3\mathrm{cm}$
C.$4\mathrm{cm}$、$4\mathrm{cm}$、$4\mathrm{cm}$
D.$2\mathrm{cm}$、$3\mathrm{cm}$、$5\mathrm{cm}$
答案:
A
6. 小明同学在学习了全等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以作出一个角的平分线.如图,一把直尺压住射线$OB$,另一把直尺压住射线$OA并且与第一把直尺交于点P$,小明说:“射线$OP就是\angle BOA$的角平分线.”小明的理论依据是

在角的内部,到角两边距离相等的点在角的平分线上
.
答案:
在角的内部,到角两边距离相等的点在角的平分线上
查看更多完整答案,请扫码查看


