《2025年配套综合练习甘肃八年级数学上册华师大版》

边边边基本事实
如果两个三角形的三条边分别对应相等,那么这两个三角形全等. 简记为“SSS”或“边边边”.

答案： SSS

【典例1】如图,$AC = DF$,$BC = EF$,$AD = BE$,$\angle BAC = 80^{\circ}$,$\angle F = 60^{\circ}$,则$\angle ABC$等于(40°)


A.$80^{\circ}$
B.$60^{\circ}$
C.$40^{\circ}$
D.$20^{\circ}$

答案： 解析：$\because AD = BE$,$\therefore AD + AE = BE + AE$,即$DE = AB$.
$\because在\triangle BAC和\triangle EDF$中,$\begin{cases}AB = DE, \\ AC = DF, \\ BC = EF,\end{cases} $
$\therefore \triangle BAC \cong \triangle EDF(SSS)$,
$\therefore \angle B = \angle DEF$,$\angle BAC = \angle D$,$\angle C = \angle F$.
$\because \angle BAC = 80^{\circ}$,$\angle F = 60^{\circ}$,
$\therefore \angle ABC = 180^{\circ} - \angle BAC - \angle C = 40^{\circ}$.

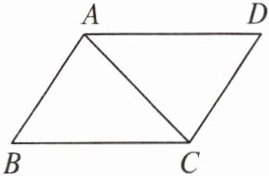
1. 如图,若$AB = CD$,$BC = AD$,则$\triangle ABC \cong \triangle$CDA,理由是SSS.

答案： CDA SSS

【典例2】如图,两根长$12m$的绳子,一端系在旗杆上的同一位置,另一端分别固定在地面上的两个木桩上(绳结处的误差忽略不计),现在只有一把卷尺,如何检验旗杆是否垂直于地面？请说明理由.

答案： 解析：用卷尺测量出$BD$、$CD$,看它们是否相等,若$BD = CD$,则$AD \perp BC$.
理由如下：
$\because在\triangle ABD和\triangle ACD$中,
$\begin{cases}AB = AC, \\ BD = CD, \\ AD = AD,\end{cases} $
$\therefore \triangle ABD \cong \triangle ACD(SSS)$,
$\therefore \angle ADB = \angle ADC$.
又$\because \angle ADB + \angle ADC = 180^{\circ}$,
$\therefore \angle ADB = \angle ADC = 90^{\circ}$,即$AD \perp BC$.

2. 如图,$CA = CB$,$AD = BD$,$M$、$N分别是CA$、$CB$的中点. 若$\triangle ADM的面积为3$,则图中阴影部分的面积为6.

答案： 6