第24页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
6. 根据图1的面积可以说明的多项式乘法运算是$(2a + b)(a + b) = 2a^{2} + 3ab + b^{2}$,那么根据图2的面积可以说明的多项式乘法运算是(
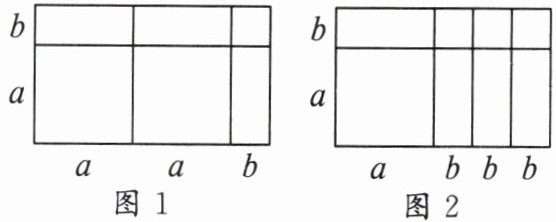
A.$(a + 3b)(a + b) = a^{2} + 4ab + 3b^{2}$
B.$(a + 3b)(a + b) = a^{2} + 3b^{2}$
C.$(b + 3a)(b + a) = b^{2} + 4ab + 3a^{2}$
D.$(a + 3b)(a - b) = a^{2} + 2ab - 3b^{2}$
A
)
A.$(a + 3b)(a + b) = a^{2} + 4ab + 3b^{2}$
B.$(a + 3b)(a + b) = a^{2} + 3b^{2}$
C.$(b + 3a)(b + a) = b^{2} + 4ab + 3a^{2}$
D.$(a + 3b)(a - b) = a^{2} + 2ab - 3b^{2}$
答案:
A
7. 如图,现有$A$类、$B类正方形卡片和C$类长方形卡片各若干张,若要拼一个长为$(3a + b)$、宽为$(a + 2b)$的大长方形,则需要

7
张$C$类卡片。
答案:
7
8. 若梯形的上底长为$a + 2b$,下底长为$2a + 3b$,高为$a + b$,则梯形的面积为
$\frac{3}{2}a^{2}+4ab+\frac{5}{2}b^{2}$
。
答案:
$\frac{3}{2}a^{2}+4ab+\frac{5}{2}b^{2}$
9. 计算:(1)$(2x + 3y)(3x - 2y)$;
(2)$(x + 2)(x - 1) - (x - 2)(x + 3)$。
(2)$(x + 2)(x - 1) - (x - 2)(x + 3)$。
答案:
解:
(1)原式$=6x^{2}-4xy+9xy-6y^{2}=6x^{2}+5xy-6y^{2}$.
(2)原式$=x^{2}+x-2-(x^{2}+x-6)=4$.
(1)原式$=6x^{2}-4xy+9xy-6y^{2}=6x^{2}+5xy-6y^{2}$.
(2)原式$=x^{2}+x-2-(x^{2}+x-6)=4$.
10. 若$(x^{2} + px - \frac{1}{3})(x^{2} - 3x + q)的积中不含x项与x^{3}$项。
(1)求$p$、$q$的值;
(2)求代数式$(- 2p^{2}q)^{2} + (3pq)^{10} + p^{2022}q^{2024}$的值。
(1)求$p$、$q$的值;
(2)求代数式$(- 2p^{2}q)^{2} + (3pq)^{10} + p^{2022}q^{2024}$的值。
答案:
解:
(1)$(x^{2}+px-\frac{1}{3})(x^{2}-3x+q)=x^{4}-3x^{3}+qx^{2}+px^{3}-3px^{2}+pqx-\frac{1}{3}x^{2}+x-\frac{1}{3}q=x^{4}+(-3+p)x^{3}+(q-3p-\frac{1}{3})x^{2}+(pq+1)x-\frac{1}{3}q$.
∵积中不含x项与$x^{3}$项,
∴$-3+p=0,pq+1=0$,解得$p=3,q=-\frac{1}{3}$.
(2)由
(1),得$pq=-1$.$(-2p^{2}q)^{2}+(3pq)^{10}+p^{2022}q^{2024}=4p^{2}(pq)^{2}+(3pq)^{10}+(pq)^{2022}q^{2}=4×3^{2}×(-1)^{2}+(-1×3)^{10}+(-1)^{2022}×(-\frac{1}{3})^{2}=36+3^{10}+\frac{1}{9}=3^{10}+36\frac{1}{9}$.
(1)$(x^{2}+px-\frac{1}{3})(x^{2}-3x+q)=x^{4}-3x^{3}+qx^{2}+px^{3}-3px^{2}+pqx-\frac{1}{3}x^{2}+x-\frac{1}{3}q=x^{4}+(-3+p)x^{3}+(q-3p-\frac{1}{3})x^{2}+(pq+1)x-\frac{1}{3}q$.
∵积中不含x项与$x^{3}$项,
∴$-3+p=0,pq+1=0$,解得$p=3,q=-\frac{1}{3}$.
(2)由
(1),得$pq=-1$.$(-2p^{2}q)^{2}+(3pq)^{10}+p^{2022}q^{2024}=4p^{2}(pq)^{2}+(3pq)^{10}+(pq)^{2022}q^{2}=4×3^{2}×(-1)^{2}+(-1×3)^{10}+(-1)^{2022}×(-\frac{1}{3})^{2}=36+3^{10}+\frac{1}{9}=3^{10}+36\frac{1}{9}$.
11.(推理能力、运算能力)欢欢与乐乐两人共同计算$(2x + a)(3x + b)$,欢欢抄错为$(2x - a)(3x + b)$,得到的结果为$6x^{2} - 13x + 6$;乐乐抄错为$(2x + a)(x + b)$,得到的结果为$2x^{2} - x - 6$。
(1)式子中的$a$、$b$的值各是多少?
(2)请计算出原题的正确答案。
(1)式子中的$a$、$b$的值各是多少?
(2)请计算出原题的正确答案。
答案:
解:
(1)根据题意可知,由于欢欢抄错了第一个多项式中的a的符号,得到的结果为$6x^{2}-13x+6$,那么$(2x-a)(3x+b)=6x^{2}+(2b-3a)x-ab=6x^{2}-13x+6$,可得$2b-3a=-13$ ①,乐乐由于漏抄了第二个多项式中的x的系数,得到的结果为$2x^{2}-x-6$,可知$(2x+a)(x+b)=2x^{2}-x-6$,即$2x^{2}+(2b+a)x+ab=2x^{2}-x-6$,可得$2b+a=-1$ ②,解关于①②的方程组,可得$a=3,b=-2$.
(2)正确的式子:$(2x+3)(3x-2)=6x^{2}+5x-6$.
(1)根据题意可知,由于欢欢抄错了第一个多项式中的a的符号,得到的结果为$6x^{2}-13x+6$,那么$(2x-a)(3x+b)=6x^{2}+(2b-3a)x-ab=6x^{2}-13x+6$,可得$2b-3a=-13$ ①,乐乐由于漏抄了第二个多项式中的x的系数,得到的结果为$2x^{2}-x-6$,可知$(2x+a)(x+b)=2x^{2}-x-6$,即$2x^{2}+(2b+a)x+ab=2x^{2}-x-6$,可得$2b+a=-1$ ②,解关于①②的方程组,可得$a=3,b=-2$.
(2)正确的式子:$(2x+3)(3x-2)=6x^{2}+5x-6$.
查看更多完整答案,请扫码查看


