第44页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
全等三角形
- 定义:能够
- 性质
全等三角形的对应边相等
全等三角形的对应角相等
- 判定:在边或角中,只有两个元素对应相等,这两个三角形不一定全等
- 定义:能够
完全重合
的两个三角形是全等三角形- 性质
全等三角形的对应边相等
全等三角形的对应角相等
- 判定:在边或角中,只有两个元素对应相等,这两个三角形不一定全等
答案:
完全重合
【典例1】如图,点B、D、E、C在一条直线上,若△ABD≌△ACE,BC= 12,BD= 3,则DE的长为(
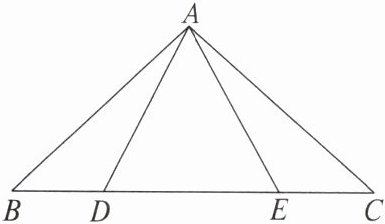
A.9
B.6
C.5
D.7
6
)
A.9
B.6
C.5
D.7
答案:
解析:
∵△ABD≌△ACE,BD= 3,
∴BD= CE= 3.
∵BC= 12,
∴DE= BC-BD-CE= 12-3-3= 6.
B
∵△ABD≌△ACE,BD= 3,
∴BD= CE= 3.
∵BC= 12,
∴DE= BC-BD-CE= 12-3-3= 6.
B
1. 如图,△ABC≌△AED,那么图中相等的角有(
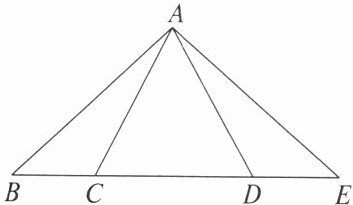
A.3对
B.4对
C.5对
D.6对
C
)
A.3对
B.4对
C.5对
D.6对
答案:
C
【典例2】如图,△FAB≌△ECD,则将△FAB通过哪种基本变换可得△ECD(
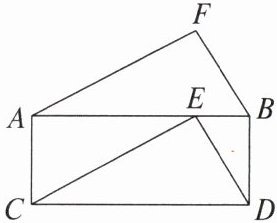
A.平移
B.翻折
C.旋转
D.无论如何都不能
A
)
A.平移
B.翻折
C.旋转
D.无论如何都不能
答案:
解析:
∵AB//CD,AF//CE,
∴△CED也可以看作是△AFB向下平移AC的单位长度所得.
A
∵AB//CD,AF//CE,
∴△CED也可以看作是△AFB向下平移AC的单位长度所得.
A
2. 如图,两个全等的直角三角形重叠在一起,将其中的一个三角形沿着点B到C的方向平移到△DEF的位置,AB= 7,DP= 3,平移距离为4,则阴影部分的面积为
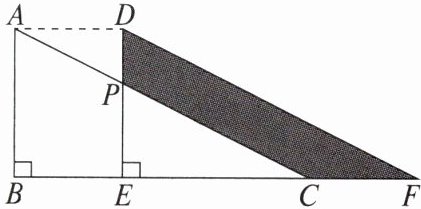
22
.
答案:
22
1. 已知图中的两个三角形全等,则∠α的度数是(
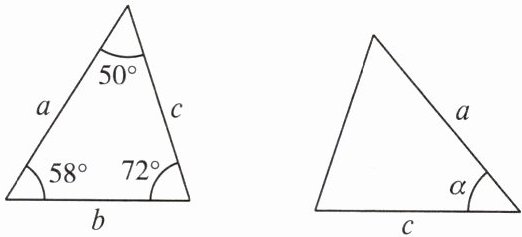
A.72°
B.60°
C.58°
D.50°
D
)
A.72°
B.60°
C.58°
D.50°
答案:
D
查看更多完整答案,请扫码查看


