《2025年阳光课堂金牌练习册七年级数学上册人教版》

9. 某餐厅中,1 张桌子可以坐 6 人,如果把多张桌子摆在一起,可以有以下两种摆放方式.

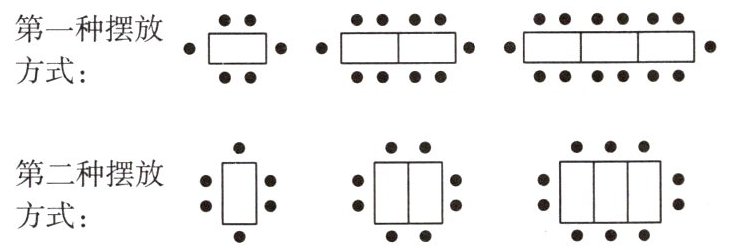
(1)当有 5 张桌子时,第一种摆放方式能坐多少人？第二种摆放方式能坐多少人？
(2)当有$n$张桌子时,用代数式分别表示第一种摆放方式和第二种摆放方式能坐的人数.

答案： 【解】
(1)第一种摆放方式,1张桌子能坐6人,每增加1张桌子,可多坐4人,所以有5张桌子时,能坐$6+4×4=22$(人).第二种摆放方式,1张桌子能坐6人,每增加1张桌子,可多坐2人,所以有5张桌子时,能坐$6+2×4=14$(人).
(2)当只有1张桌子时,第一种摆放方式坐6人,后边多1张桌子多坐4人.故有n张桌子时,能坐$[6+4(n-1)]$人.当只有1张桌子时,第二种摆放方式坐6人,后边多1张桌子多坐2人.故有n张桌子时能坐$[6+2(n-1)]$人.

【典型例题1】下列相关的量中,成反比例关系的是(A)
A.平行四边形的面积一定,底和高
B.圆的周长与面积
C.正方形的周长与边长
D.圆锥的体积一定,圆锥的底面半径与高

答案： A

1. 某种报刊售价固定不变,购买该报刊的份数和钱数成什么比例关系？(A)
A.成正比例关系
B.成反比例关系
C.不成比例关系
D.无法确定

答案： A

2. 下列各种关系中,成反比例关系的是(B)
A.若5x= 8y,则x和y的关系
B.铺地面积一定,每块砖的面积和用砖块数
C.在同时同地条件下,竹竿的长和它的影长
D.同学的年龄一定,他们的身高与体重

答案： B 【解析】因为5x=8y,即x:y=8/5,所以y和x成正比例关系;因为每块砖的面积×铺地砖块数=铺地面积(一定),积一定,所以每块砖的面积与铺地砖块数成反比例关系;因为同时同地条件下,竹竿的长和它的影长,比值一定,所以同时同地条件下,竹竿的长与它的影长成正比例关系;同学的年龄一定,他们的身高与体重的比值不一定,乘积也不一定,所以他们的身高与体重不成比例关系.故选B.